Kerr Metrik

[Yukterez]

Das ist die deutschsprachige Version.   English versions are available on en.yukterez.net and yukipedia.

Verwandte Beiträge: Kerr Newman || Schwarzschild || De Sitter || Feldgleichungen || Gravitationslinsen || Raytracer || Flamm



Schatten und Oberflächen (letztere sind fürs Auge unsichtbar) eines rotierenden schwarzen Lochs (Spin a=1). Zoom out: [-], Konturen: ƒ


Schatten und Oberflächen eines schwarzen Lochs (a=0.99) für verschiedene Polneigungswinkel (θ=1°..90°). Verlangsamen: ⎆


Akkretionsscheibe mit Innen- und Außenradius ri=isco und ra=7 um ein SL mit a=0.95, Beobachter auf r=100, Betrachtungswinkel: θ=70°

[Yukterez]

Alle Formeln sind in den natürlichen Einheiten G=M=c=1, d.h. alle Längen haben die Einheit GM/c² und Zeiten GM/c³. Die metrische Signatur ist time-positive (+,-,-,-). Dabei ist a der Spinparameter (für schwarze Löcher 0≤a≤M), M das gesamte Massenäquivalent des Zentralkörpers, und Mirr seine irreduzible Masse:

Die zusammengefassten Terme sind



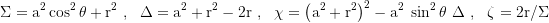
Kovariante metrische Koeffizienten:



Kontravariante Metrik-Komponenten (hochgestellte Buchstaben sind hierbei keine Potenzen sondern Indizes):



Dabei steht a für den dimensionslosen Spinparameter Jc/G/M². Mit der Transformationsregel in kartesische Koordinaten:



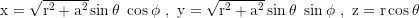
lautet das Linienelement in Boyer-Lindquist-Koordinaten:



Metrischer Tensor (t,r,θ,Ф):



Mit a=0 reduzieren sich Boyer Lindquist Koordinaten auf klassische Schwarzschild Koordinaten. Die Koordinatenzeit entspricht der Eigenzeit eines Beobachters at infinity.


Μit der Transformation:



mit der Koordinatenzeit T und dem Azimuthalwinkel ψ:



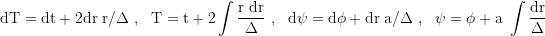
lautet die Metrik in Kerr-Schild-Koordinaten (T,r,θ,ψ):



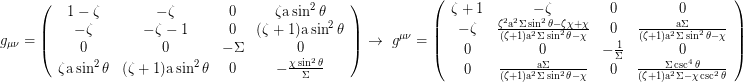
Mit a=0 reduzieren sich Kerr Schild Koordinaten auf erweiterte Eddington Finkelstein Koordinaten. Die Koordinatenzeit wird durch radial einfallende Lichtstrahlen synchronisiert.


Bewegungsgleichungen in Boyer-Lindquist-Koordinaten:


Ko- und kontravariante Impulskomponenten:



Koordinatenzeit abgeleitet nach der Eigenzeit (dt/dτ):



Zeitliche Impulskomponente:



Radiale Koordinate abgeleitet nach der Eigenzeit (dr/dτ):



Radiale Impulskomponente abgeleitet nach der Eigenzeit:



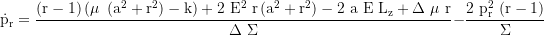
Radialer Impuls:



Breitengrad abgeleitet nach der Eigenzeit (dθ/dτ):



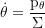
Poloidiale (longitudinale) Drehimpulskomponente abgeleitet nach der Eigenzeit (dpθ/dτ):



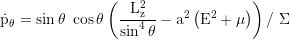
Longitudinale Drehimpulskomponente:



Längengrad abgeleitet nach der Eigenzeit (dФ/dτ):



Äquatoriale (latitudinale) Drehimpulskomponente:



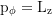
Der latitudinale Drehimpuls ist eine Erhaltungsgröße:



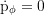
Erhaltungsgröße Carter-Konstante:



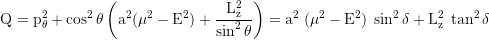
Erhaltungsgröße Carter k:



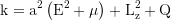
Erhaltungsgröße Gesamtenergie:



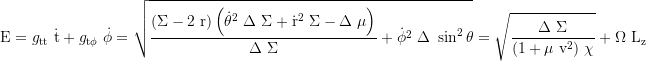
Erhaltungsgröße Drehimpuls entlang Ф:



Lokale 3er-Geschwindigkeit auf der r-Achse:



Lokale 3er-Geschwindigkeit auf der θ-Achse:



Lokale 3er-Geschwindigkeit auf der Ф-Achse:



Lokale 3er-Geschwindigkeit, total:



Für massebehaftete Testteilchen gilt μ=-1 und für Photonen μ=-0. a ist der Spinparameter und δ der Bahninklinationswinkel. Mit α als dem vertikalen Abschusswinkel ergeben sich die Komponenten der Geschwindigkeit (relativ zum ZAMO)



Aus der Unendlichkeit beobachtete Geschwindigkeit:

Radiale Fluchtgeschwindigkeit:



Radiales Effektives Potential:

Frame-Dragging Winkelgeschwindigkeit (dФ/dt); assumed ein SL Trägheitsmoment von I=2r²/3 (hohle Sphäre):

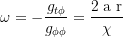
Verzögerte Frame-Dragging Transversalgeschwindigkeit am Äquator des äußeren Horizonts:



mit dem Horizont- und Ergosphärenradius (Lösung für r bei Δ=0 und gtt=0):



Von r und θ abhängige verzögerte Frame-Dragging Transversalgeschwindigkeit:



Auf der äquatorialen Ebene mit θ=π/2:



Von r und θ abhängige lokale Frame-Dragging Transversalgeschwindigkeit (ab der Ergosphäre >c):



Auf der äquatorialen Ebene mit θ=π/2:



Auf die kartesischen Hintergrundkoordinaten projizierte Frame-Dragging Transversalgeschwindigkeit:



Auf der äquatorialen Ebene mit θ=π/2:

Gravitative Zeitdilatationskomponente (dt/dτ):



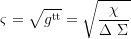
Axialer und koaxialer Gyrationsradius:



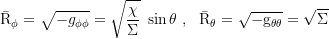
Axialer und koaxialer Umfang:



Der letzte stabile Orbit (ISCO) liegt bei



mit den abkürzenden Termen

Beispiel 1:



Bahn eines Photons durch die Ringsingularität und Austritt im Antiversum; Startbedingungen: r0=7, θ0=π/4, v0=vr0=c (radial einfallendes Photon). Bahnkonstanten: E total=0.8469 hf0, Carter Q=-0.29 GMhf0/c³, Lz=0 GMhf0/c³, Spin: a=0.9 M.

Untere Hälfte: Boyer-Lindquist-Koordinaten (die darstellbare Bahn endet an der Koordinatensingularität am äußeren Ereignishorizont, wo der Partikel mit stehengebliebener Uhr am rotierenden Ereignishorizont einfriert und im System des weit entfernten Beobachters unendlich viele Korotationen ausführt).

Obere Hälfte: die selbe Situation in Kerr-Schild-Koordinaten (die Bahn kann damit bis zur Ringsingularität und darüber hinaus fortgesetzt werden, da die infinite Korotation heraustransformiert und die unendlich vielen Umdrehungen in infinitesimaler Eigenzeit am Horizont dadurch vermieden werden). Animationsparameter: affiner Nullgeodätenparameter.

Beispiel 2:



Lokal retrograde Kreisbahn eines Testpartikels im inneren eines mit a=0.99 rotierenden schwarzen Lochs (innerhalb des Cauchyhorizonts, aber außerhalb der inneren Ergosphäre sind wieder radial konstante Orbits möglich, für eine nähere Erklärung siehe hier).

Für weitere Beispiele geht es hier entlang.

[Yukterez]

#1 Simulator Code, Boyer-Lindquist & Kerr-Schild, Partikel & Photonen (für Doran Koordinaten klick hier):

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||| Mathematica Syntax | kerr.yukterez.net | 22.06.2016 - 04.04.2019, Version 17 |||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
mt1 = {"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mt2 = {"EventLocator", "Event"-> (r[τ]-1001/1000 rA)};
mt3 = {"ImplicitRungeKutta", "DifferenceOrder"-> 20};
mt4 = {"EquationSimplification"-> "Residual"};
mt0 = Automatic;
mta = mt0;                                                   (* mt0: Speed, mt3: Accuracy *)
wp  = MachinePrecision;
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 1) STARTBEDINGUNGEN EINGEBEN |||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
A   = a;                                         (* pseudosphärisch: A=0, kartesisch: A=a *)
crd = 1;                                    (* Boyer-Lindquist: crd=1, Kerr-Schild: crd=2 *)
dsp = 1;                                                                 (* Display Modus *)
 
tmax = 120;                                                                  (* Eigenzeit *)
Tmax = 120;                                                            (* Koordinatenzeit *)
TMax = Min[Tmax, т[plunge-1*^-3]]; tMax = Min[tmax, plunge];          (* Integrationsende *)
 
r0 = 3;                                                                    (* Startradius *)
r1 = 5;                                                      (* Endradius wenn v0=vr0=vr1 *)
θ0 = π/2;                                                                  (* Breitengrad *)
φ0 = 0;                                                                     (* Längengrad *)
a  = 1;                                                                  (* Spinparameter *)
 
v0 = 1;                                                         (* Anfangsgeschwindigkeit *)
α0 = 0;                                                      (* vertikaler Abschusswinkel *)
ψ0 = δp[r0, a];                                                 (* Bahninklinationswinkel *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 2) GESCHWINDIGKEITS-, ENERGIE UND DREHIMPULSKOMPONENTEN ||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
vr0 = v0 Sin[α0];                                   (* radiale Geschwindigkeitskomponente *)
vθ0 = v0 Cos[α0] Sin[ψ0];                    (* longitudinale  Geschwindigkeitskomponente *)
vφ0 = v0 Cos[α0] Cos[ψ0];                      (* latitudinale Geschwindigkeitskomponente *)

vrj[τ_]:=R'[τ]/Sqrt[Δi[τ]] Sqrt[Σi[τ] (1+μ v[τ]^2)];
vθj[τ_]:=Θ'[τ] Sqrt[Σi[τ] (1+μ v[τ]^2)];
vφBL[τ_]:=-((Sin[Θ[τ]] Sqrt[1+μ v[τ]^2] (-a^5 ε Cos[Θ[τ]]^2-a ε R[τ]^4+
a^2 Δi[τ] (xJ[τ] ε Cot[Θ[τ]]^2+Φ'[τ] Cos[Θ[τ]]^2 Σi[τ])+
R[τ]^2 (-a^3 ε (1+Cos[Θ[τ]]^2)+Δi[τ] (xJ[τ] ε Csc[Θ[τ]]^2+Φ'[τ] Σi[τ]))))/((a^2 Cos[Θ[τ]]^2+
R[τ]^2) (a^2 Sin[Θ[τ]]^2-Δi[τ]) Sqrt[Χi[τ]/Σi[τ]]));
vφKS[τ_]:=(j[v[τ]] Sin[Θ[τ]]^2 (2 a ε R[τ]-Φ'[τ] Δi[τ] Σi[τ]+
a Σi[τ] R'[τ]))/(Ыi[τ] (2 R[τ]-Σi[τ]))
vφj[τ_]:=If[crd==2, vφKS[τ], vφBL[τ]];

vtj[τ_]:=Sqrt[vrj[τ]^2+vθj[τ]^2+vφj[τ]^2];
vr[τ_]:=vrj[τ]/vtj[τ]*v[τ];
vθ[τ_]:=vθj[τ]/vtj[τ]*v[τ];
vφ[τ_]:=vφj[τ]/vtj[τ]*v[τ];
 
x0BL[A_] := Sqrt[r0^2+A^2] Sin[θ0] Cos[φ0];                         (* Anfangskoordinaten *)
y0BL[A_] := Sqrt[r0^2+A^2] Sin[θ0] Sin[φ0];
z0[A_] := r0 Cos[θ0];
 
x0KS[A_] := ((r0 Cos[φ0]+A Sin[φ0]) Sin[θ0]);
y0KS[A_] := ((r0 Sin[φ0]-A Cos[φ0]) Sin[θ0]);
 
x0[A_] := If[crd==1, x0BL[A], x0KS[A]];
y0[A_] := If[crd==1, y0BL[A], y0KS[A]];
 
ε   = Sqrt[δ Ξ/χ]/j[v0]+Lz ω0;                       (* Energie und Drehimpulskomponenten *)
Lz  = vφ0 Ы/j[v0];
pθ0 = vθ0 Sqrt[Ξ]/j[v0];
pr0 = vr0 Sqrt[(Ξ/δ)/j[v0]^2];
Q   = Simplify[Limit[pθ0^2+(Lz^2 Csc[ϑ]^2-a^2 (ε^2+μ)) Cos[ϑ]^2, ϑ->θ0]];     (* Carter Q *)
k   = Q+Lz^2+a^2 (ε^2+μ);                                                     (* Carter k *)
μ   = If[Abs[v0]==1, 0, -1];                                 (* Baryon: μ=-1, Photon: μ=0 *)

 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 3) RADIUS NACH GESCHWINDIGKEIT UND VICE VERSA ||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
rPro = 2 (1+Cos[2/3 ArcCos[-a]]);                        (* prograder Photonenorbitradius *)
rRet = 2 (1+Cos[2/3 ArcCos[+a]]);                      (* retrograder Photonenorbitradius *)
rTeo = 1+2 Sqrt[1-a^3/3] Cos[ArcCos[(1-a^2)/(1-a^2/3)^(3/2)]/3];
                                                                                  (* ISCO *)
isco = rISCO/.Solve[0 == rISCO (6 rISCO-rISCO^2+3 a^2)-8 a rISCO^(3/2) && rISCO>=rA, rISCO][[1]];
 
δp[r_,a_] := Quiet[δi/.NSolve[(a^4(-1+r)+2(-3+r)r^4+a^2r(6+r(-5+3 r))+ (* Eq. Ink. Winkel *)
4a Sqrt[a^2+(-2+r)r](a^2+3 r^2)Cos[δi]-a^2(3+r)(a^2+(-2+r)r)Cos[2δi])/(2r(a^2+
(-2+r)r)(r^3+a^2(2+r)))==0&&δi<=π&&δi>=0,δi][[1]]];
 
vPro = (a^2-2a Sqrt[r0]+r0^2)/(Sqrt[a^2+(-2+r0)r0](a+r0^(3/2)));(* Kreisgeschwindigkeit + *)
vRet = (a^2+2a Sqrt[r0]+r0^2)/(Sqrt[a^2+(-2+r0)r0](a-r0^(3/2)));(* Kreisgeschwindigkeit - *)
vr1  = \[Sqrt](((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2) ((a^2+r1^2)^2-a^2 (a^2+(-2+
r1) r1) Sin[θ0]^2) (-1+((a^2+(-2+r1) r1) (r1^2+a^2 Cos[θ0]^2) (-(a^2+r0^2)^2+
a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))/((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2) (-(a^2+
r1^2)^2+a^2 (a^2+(-2+r1) r1) Sin[θ0]^2))))/((a^2+(-2+r1) r1) (r1^2+
a^2 Cos[θ0]^2) ((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))); (* v Flucht von r0 bis r1 *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 4) HORIZONTE UND ERGOSPHÄREN RADIEN ||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
rE = 1+Sqrt[1-a^2 Cos[θ]^2];                                         (* äußere Ergosphäre *)
rG = 1-Sqrt[1-a^2 Cos[θ]^2];                                         (* innere Ergosphäre *)
rA = 1+Sqrt[1-a^2];                                                   (* äußerer Horizont *)
rI = 1-Sqrt[1-a^2];                                                   (* innerer Horizont *)
 
RE[A_, w1_, w2_] := Xyz[xyZ[
{Sqrt[rE^2+A^2] Sin[θ] Cos[φ], Sqrt[rE^2+A^2] Sin[θ] Sin[φ], rE Cos[θ]}, w1], w2];
RG[A_, w1_, w2_] := Xyz[xyZ[
{Sqrt[rG^2+A^2] Sin[θ] Cos[φ], Sqrt[rG^2+A^2] Sin[θ] Sin[φ], rG Cos[θ]}, w1], w2];
RA[A_, w1_, w2_] := Xyz[xyZ[
{Sqrt[rA^2+A^2] Sin[θ] Cos[φ], Sqrt[rA^2+A^2] Sin[θ] Sin[φ], rA Cos[θ]}, w1], w2];
RI[A_, w1_, w2_] := Xyz[xyZ[
{Sqrt[rI^2+A^2] Sin[θ] Cos[φ], Sqrt[rI^2+A^2] Sin[θ] Sin[φ], rI Cos[θ]}, w1], w2];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 5) HORIZONTE UND ERGOSPHÄREN PLOT ||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

horizons[A_, mesh_, w1_, w2_] := Show[
ParametricPlot3D[RE[A, w1, w2], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> mesh, PlotPoints -> plp, PlotStyle -> Directive[Blue, Opacity[0.10]]],
ParametricPlot3D[RA[A, w1, w2], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> plp, PlotStyle -> Directive[Cyan, Opacity[0.15]]],
ParametricPlot3D[RI[A, w1, w2], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> plp, PlotStyle -> Directive[Red, Opacity[0.25]]],
ParametricPlot3D[RG[A, w1, w2], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> plp, PlotStyle -> Directive[Red, Opacity[0.35]]]];
BLKS := Grid[{{horizons[a, 35, 0, 0], horizons[0, 35, 0, 0]}}];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 6) FUNKTIONEN ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
j[v_]  := Sqrt[1+μ v^2];                                                 (* Lorentzfaktor *)
mirr    = Sqrt[(Sqrt[1-a^2]+1)/2];                                   (* irreduzible Masse *)
я       = Sqrt[Χ/Σ]Sin[θ[τ]];                                    (* axialer Umfangsradius *)
яi[τ_] := Sqrt[Χi[τ]/Σi[τ]]Sin[Θ[τ]];

Ы       = Sqrt[χ/Ξ]Sin[θ0];
Ыi[τ_] := Sqrt[Χi[τ]/Σi[τ]]Sin[Θ[τ]];
ц       = 2r[τ]/Σ; ц0=2r0/Ξ;
 
Σ       = r[τ]^2+a^2 Cos[θ[τ]]^2;                            (* poloidialer Umfangsradius *)
Σi[τ_] := R[τ]^2+a^2 Cos[Θ[τ]]^2;
Ξ       = r0^2+a^2 Cos[θ0]^2;
 
Δ       = r[τ]^2-2r[τ]+a^2;
Δi[τ_] := R[τ]^2-2R[τ]+a^2;
δ       = r0^2-2r0+a^2;
 
Χ       = (r[τ]^2+a^2)^2-a^2 Sin[θ[τ]]^2 Δ;
Χi[τ_] := (R[τ]^2+a^2)^2-a^2 Sin[Θ[τ]]^2 Δi[τ];
χ       = (r0^2+a^2)^2-a^2 Sin[θ0]^2 δ;

XJ      = a Sin[θ[τ]]^2;
xJ[τ_] := a Sin[Θ[τ]]^2;
Xj      = a Sin[θ0]^2;
 
т[τ_] := Evaluate[t[τ]/.sol][[1]];                      (* Koordinatenzeit nach Eigenzeit *)
д[ξ_] := Quiet[Ξ /.FindRoot[т[Ξ]-ξ, {Ξ, 0}]];           (* Eigenzeit nach Koordinatenzeit *)
T := Quiet[д[tk]];                       
 
ю[τ_] := Evaluate[t'[τ]/.sol][[1]];
γ[τ_] := If[μ==0, "Infinity", ю[τ]];                                         (* totale ZD *)
R[τ_] := Evaluate[r[τ]/.sol][[1]];                              (* Boyer-Lindquist Radius *)
Φ[τ_] := Evaluate[φ[τ]/.sol][[1]];                           
Θ[τ_] := Evaluate[θ[τ]/.sol][[1]];
ß[τ_] := Re[Sqrt[X'[τ]^2+Y'[τ]^2+Z'[τ]^2 ]/ю[τ]];
 
gs[τ_] := (2 (R[τ]^2-a^2 Cos[Θ[τ]]^2) Sqrt[((a^2+R[τ]^2)^2-a^2 (a^2+(R[τ]- (* Gravitation *)
2) R[τ]) Sin[Θ[τ]]^2)/(a^2+2 R[τ]^2+a^2 Cos[2 Θ[τ]])^2])/(R[τ]^2+a^2 Cos[Θ[τ]]^2)^2;
 
ς[τ_] := Sqrt[Χi[τ]/Δi[τ]/Σi[τ]]; ς0 = Sqrt[χ/δ/Ξ];                     (* gravitative ZD *)
ω[τ_] := 2R[τ] a/Χi[τ];           ω0 = 2r0 a/χ; ωd=2r[τ] a/Χ;           (* Frame Dragging *)
Ω[τ_] := ω[τ] Sqrt[X[τ]^2+Y[τ]^2];          (* Frame Dragging beobachtete Geschwindigkeit *)
й[τ_] := ω[τ] яi[τ] ς[τ];         й0 = ω0 Ы ς0;  (* Frame Dragging lokale Geschwindigkeit *)
 
ж[τ_] := Sqrt[ς[τ]^2-1]/ς[τ];     ж0 = Sqrt[ς0^2-1]/ς0;          (* Fluchtgeschwindigkeit *)
                           vEsc = ж0;
     
vd[τ_] := Abs[-((\[Sqrt](-a^4(ε-Lz ωd)^2-2 a^2r[τ]^2 (ε-Lz ωd)^2-
        r[τ]^4(ε-Lz ωd)^2+Δ(Σ+a^2 Sin[θ[τ]]^2 (ε-
        Lz ωd)^2)))/(Sqrt[-(a^2+r[τ]^2)^2+
        a^2 Sin[θ[τ]]^2 Δ](ε - Lz ωd)))];     
   
v[τ_]   := If[μ==0, 1, Evaluate[vlt'[τ]/.sol][[1]]];      (* lokale Dreiergeschwindigkeit *)
dst[τ_] := Evaluate[str[τ]/.sol][[1]];                                         (* Strecke *)
     
pΘ[τ_] := Evaluate[pθ[τ] /. sol][[1]]; pΘks[τ_] := Σi[τ] Θ'[τ];                 (* Impuls *)
pR[τ_] := Evaluate[pr[τ] /. sol][[1]]; pRks[τ_] := Σi[τ]/Δi[τ] R'[τ];
sh[τ_] := Re[Sqrt[ß[τ]^2-Ω[τ]^2]];
epot[τ_] := ε+μ-ekin[τ];                                           (* potentielle Energie *)
ekin[τ_] := If[μ==0, ς[τ], 1/Sqrt[1-v[τ]^2]-1];                     (* kinetische Energie *)
 
                                                               (* beobachtete Inklination *)
ink0 := б/. Solve[Z'[0]/ю[0] Cos[б]==-Y'[0]/ю[0] Sin[б]&&б>0&&б<2π&&б<δp[r0, a], б][[1]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 7) DIFFERENTIALGLEICHUNG |||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
dp= Style[\!\(\*SuperscriptBox[\(Y\),\(Y\)]\), White]; n0[z_] := Chop[Re[N[Simplify[z]]]];
 
(* Boyer-Lindquist-Koordinaten *)
 
pr2τ[τ_] := 1/(Σ Δ) (((r[τ]^2+a^2)μ-k)(r[τ]-1)+r[τ] Δ μ+2r[τ](r[τ]^2+a^2) ε^2-
2 a ε Lz)-(2pr[τ]^2 (r[τ]-1))/Σ;
pθ2τ[τ_] := (Sin[θ[τ]]Cos[θ[τ]])/Σ (Lz^2/Sin[θ[τ]]^4-a^2 (ε^2+μ));
                                         
DG1={
t'[τ]  == ε+(2r[τ](r[τ]^2+a^2)ε-2 a r[τ] Lz)/(Σ Δ),
t[0]   == 0,
 
r'[τ]  == (pr[τ] Δ)/Σ,
r[0]   == r0,
 
θ'[τ]  == pθ[τ]/Σ,
θ[0]   == θ0,
 
φ'[τ]  == (2 a r[τ] ε+(Σ-2r[τ])Lz Csc[θ[τ]]^2)/(Σ Δ),
φ[0]   == φ0,
 
pr'[τ] == pr2τ[τ],
pr[0]  == pr0,
 
pθ'[τ] == pθ2τ[τ],
pθ[0]  == pθ0,
 
str'[τ]== vd[τ]/Max[1*^-16, Abs[Sqrt[1-vd[τ]^2]]],
str[0] == 0,
 
vlt'[τ]== vd[τ],
vlt[0] == 0
};
 
(* Kerr-Schild-Koordinaten *)
 
dr = (pr0 δ)/Ξ; dθ=pθ0/Ξ;
dφ = (2a r0 ε+(Ξ-2r0)Lz Csc[θ0]^2)/(Ξ δ)+dr a/δ;
dΦ = If[θ0==0, 0, If[θ0==π, 0, dφ]];
φk = φ0+cns/.FindRoot[Sqrt[r0^2+a^2] Cos[φ0+cns]-((r0 Cos[φ0]+a Sin[φ0])),{cns,1}];
 
DG2={
t''[τ] == (2 ((a^4 Cos[θ[τ]]^4+a^2 Cos[θ[τ]]^2 r[τ]-r[τ]^3-r[τ]^4) r'[τ]^2+r[τ] ((a^2 Cos[θ[τ]]^2-r[τ]^2) t'[τ]^2+r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 θ'[τ]^2-2 a^3 Cos[θ[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^3 θ'[τ] φ'[τ]+Sin[θ[τ]]^2 (r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2+a^2 (a^2 Cos[θ[τ]]^2-r[τ]^2) Sin[θ[τ]]^2) φ'[τ]^2+a t'[τ] (a (2 a^2 Cos[θ[τ]]^3 Sin[θ[τ]]+r[τ]^2 Sin[2 θ[τ]]) θ'[τ]+2 (-a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^2 φ'[τ]))+r'[τ] ((a^4 Cos[θ[τ]]^4+2 a^2 Cos[θ[τ]]^2 r[τ]-2 r[τ]^3-r[τ]^4) t'[τ]+a (a r[τ] (2 a^2 Cos[θ[τ]]^3 Sin[θ[τ]]+r[τ]^2 Sin[2 θ[τ]]) θ'[τ]+(-a^4 Cos[θ[τ]]^4-2 a^2 Cos[θ[τ]]^2 r[τ]+2 r[τ]^3+r[τ]^4) Sin[θ[τ]]^2 φ'[τ]))))/(a^2 Cos[θ[τ]]^2+r[τ]^2)^3,
t'[0]  == Limit[(ц0 (-dr+a Sin[θ1]^2 dΦ))/(-1+ц0)+\[Sqrt]((1/((-1+ц0)^2 Ξ))(Ξ (dr^2+(-1+ц0) (μ-Ξ dθ^2))+Sin[θ1]^2 dΦ (-2a Ξ dr-(-1+ц0) χ dΦ+ц0^2 a^2 Ξ Sin[θ1]^2 dΦ))), θ1->θ0],
t[0]   == 0,
 
r''[τ] == (-8 (a^2 Cos[θ[τ]]^2-r[τ]^2) (a^2 Cos[2 θ[τ]]+r[τ] (2+r[τ])) r'[τ]^2+4 r'[τ] (4 (a^2 Cos[θ[τ]]^2-r[τ]^2) (-2 r[τ]+a^2 Sin[θ[τ]]^2) t'[τ]+2 a^2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 Sin[2 θ[τ]] θ'[τ]-a Sin[θ[τ]]^2 (2 r[τ] (a^2 Cos[θ[τ]]^2 (-4+a^2+a^2 Cos[2 θ[τ]])+2 r[τ] ((2+a^2+a^2 Cos[2 θ[τ]]) r[τ]+r[τ]^3-a^2 Sin[θ[τ]]^2))+a^4 Sin[2 θ[τ]]^2) φ'[τ])+2 (a^2+(-2+r[τ]) r[τ]) (4 (a^2 Cos[θ[τ]]^2-r[τ]^2) t'[τ]^2+4 r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 θ'[τ]^2+8 a (-a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^2 t'[τ] φ'[τ]+Sin[θ[τ]]^2 (4 r[τ] ((a^2 Cos[θ[τ]]^2+r[τ]^2)^2-a^2 r[τ] Sin[θ[τ]]^2)+a^4 Sin[2 θ[τ]]^2) φ'[τ]^2))/(8 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3),
r'[0]  == dr,
r[0]   == r0,
 
θ''[τ] == (4 a^2 r[τ] Sin[2 θ[τ]] (r'[τ]+t'[τ])^2-8 r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 r'[τ] θ'[τ]+2 a^2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 Sin[2 θ[τ]] θ'[τ]^2-8 a ((Cos[θ[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 Sin[θ[τ]]+r[τ] (a^2+r[τ]^2) Sin[2 θ[τ]]) r'[τ]+r[τ] (a^2+r[τ]^2) Sin[2 θ[τ]] t'[τ]) φ'[τ]+(2 a^6 Cos[θ[τ]]^4+r[τ] (a^4 Cos[θ[τ]]^2 (5+Cos[2 θ[τ]]) r[τ]+2 a^2 (2+Cos[2 θ[τ]]) r[τ]^3+2 r[τ]^5+2 a^2 (a^2 (3+Cos[2 θ[τ]])+4 r[τ]^2) Sin[θ[τ]]^2)) Sin[2 θ[τ]] φ'[τ]^2)/(4 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3),
θ'[0]  == dθ,
θ[0]   == θ0,
 
φ''[τ] == If[θ[τ]==0, 0, (4 (a^3 Cos[θ[τ]]^2-a r[τ]^2) r'[τ]^2+4 (a^3 Cos[θ[τ]]^2-a r[τ]^2) t'[τ]^2+4 a r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 θ'[τ]^2-8 (a^2 Cos[θ[τ]]^2+r[τ]^2) (Cot[θ[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2+a^2 r[τ] Sin[2 θ[τ]]) θ'[τ] φ'[τ]+a Sin[θ[τ]]^2 (4 r[τ] ((a^2 Cos[θ[τ]]^2+r[τ]^2)^2-a^2 r[τ] Sin[θ[τ]]^2)+a^4 Sin[2 θ[τ]]^2) φ'[τ]^2+8 a t'[τ] (2 Cot[θ[τ]] r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2) θ'[τ]+a (-a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^2 φ'[τ])+8 r'[τ] ((a^3 Cos[θ[τ]]^2-a r[τ]^2) t'[τ]+a Cot[θ[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2) (a^2 Cos[θ[τ]]^2+r[τ] (2+r[τ])) θ'[τ]-(r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2+a^2 (a^2 Cos[θ[τ]]^2-r[τ]^2) Sin[θ[τ]]^2) φ'[τ]))/(4 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3)],
φ'[0]  == dΦ,
φ[0]   == φk,
 
str'[τ]== vd[τ]/Max[1*^-16, Abs[Sqrt[1-vd[τ]^2]]],
str[0] == 0,
 
vlt'[τ]== vd[τ],
vlt[0] == 0
};
 
DGL = If[crd==1, DG1, DG2];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 8) INTEGRATION |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
sol=
 
NDSolve[DGL, {t, r, θ, φ, str, vlt, pr, pθ}, {τ, 0, tmax},
WorkingPrecision-> wp,
MaxSteps-> Infinity,
Method-> mta,
InterpolationOrder-> All,
StepMonitor :> (laststep=plunge; plunge=τ;
stepsize=plunge-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-4, 0, 1])}];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 9) KOORDINATEN |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
XBL[τ_] := Evaluate[Sqrt[r[τ]^2+a^2] Sin[θ[τ]] Cos[φ[τ]]/.sol][[1]];
YBL[τ_] := Evaluate[Sqrt[r[τ]^2+a^2] Sin[θ[τ]] Sin[φ[τ]]/.sol][[1]];
Z[τ_]   := Evaluate[r[τ] Cos[θ[τ]]/.sol][[1]];
 
XKS[τ_] := Evaluate[((r[τ] Cos[φ[τ]]+a Sin[φ[τ]]) Sin[θ[τ]])/.sol][[1]];
YKS[τ_] := Evaluate[((r[τ] Sin[φ[τ]]-a Cos[φ[τ]]) Sin[θ[τ]])/.sol][[1]];
 
X[τ_]   := If[crd==1, XBL[τ], XKS[τ]];
Y[τ_]   := If[crd==1, YBL[τ], YKS[τ]];
 
xBL[τ_] := Evaluate[Sqrt[r[τ]^2+A^2] Sin[θ[τ]] Cos[φ[τ]]/.sol][[1]];
yBL[τ_] := Evaluate[Sqrt[r[τ]^2+A^2] Sin[θ[τ]] Sin[φ[τ]]/.sol][[1]];
z[τ_]   := Z[τ];
 
xKS[τ_] := Evaluate[((r[τ] Cos[φ[τ]]+A Sin[φ[τ]]) Sin[θ[τ]])/.sol][[1]];
yKS[τ_] := Evaluate[((r[τ] Sin[φ[τ]]-A Cos[φ[τ]]) Sin[θ[τ]])/.sol][[1]];
 
x[τ_]   := If[crd==1, xBL[τ], xKS[τ]];
y[τ_]   := If[crd==1, yBL[τ], yKS[τ]];
 
XYZ[τ_] := Sqrt[X[τ]^2+Y[τ]^2+Z[τ]^2]; XY[τ_] := Sqrt[X[τ]^2+Y[τ]^2];   (* kartesisches R *)
 
Xyz[{x_, y_, z_}, α_] := {x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z};    (* Rotationsmatrix *)
xYz[{x_, y_, z_}, β_] := {x Cos[β]+z Sin[β], y, z Cos[β]-x Sin[β]};
xyZ[{x_, y_, z_}, ψ_] := {x, y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]};
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 10) PLOT EINSTELLUNGEN |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
PR  = 1.2 r1;                                                               (* Plot Range *)
d1  = 2;                                                                  (* Schweiflänge *)
plp = 50;                                                          (* Flächenplot Details *)
Plp = Automatic;                                                        (* Kurven Details *)
 
Mrec    = 100;                                           (* Parametric Plot Subdivisionen *)
mrec    = 10;
 
imgsize = 380;                                                               (* Bildgröße *)
w1l     = 0;                                                 (* Startperspektiven, Winkel *)
w2l     = 0;
w1r     = 0;
w2r     = 0;
 
s[text_]:=Style[text, FontFamily->"Consolas", FontSize->11];               (* Anzeigestil *)

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 11) PLOT NACH EIGENZEIT ||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
display[T_] := Grid[{
{If[μ==0, s[" affineP"], s[" τ propr"]], " = ", s[n0[tp]], s["GM/c³"], s[dp]},
{s[" t coord"], " = ", s[n0[т[tp]]], s["GM/c³"], s[dp]},
(* {s[" т coord"], " = ", s[n0[т[tp]+Sign[1.5-dsp] 2 NIntegrate[R[Ti]/(R[Ti]^2-2 R[Ti]+a^2),{Ti,0,T}]]], s["GM/c³"], s[dp]}, *)
{s[" ṫ total"], " = ", s[n0[If[dsp==1, ю[tp]-2 If[crd==1, 0, R'[tp] R[tp]/(R[tp]^2-2 R[tp]+a^2)], ю[T]]]], s[If[dsp==1, "dt/dτ", "dт/dτ"]], s[dp]},
{s[" ς gravt"], " = ", s[n0[ς[tp]]], s["dt/dτ"], s[dp]},
{s[" γ kinet"], " = ", If[μ==0, s[n0[ς[tp]]], s[n0[1/Sqrt[1-v[tp]^2]]]], s["dt/dτ"], s[dp]},
{s[" R carts"], " = ", s[n0[XYZ[tp]]], s["GM/c²"], s[dp]},
{s[" x carts"], " = ", s[n0[X[tp]]], s["GM/c²"], s[dp]},
{s[" y carts"], " = ", s[n0[Y[tp]]], s["GM/c²"], s[dp]},
{s[" z carts"], " = ", s[n0[Z[tp]]], s["GM/c²"], s[dp]},
{s[" s dstnc"], " = ", s[n0[dst[tp]]], s["GM/c²"], s[dp]},

{s[" r coord"], " = ", s[n0[R[tp]]], s["GM/c²"], s[dp]},
{s[" φ longd"], " = ", s[n0[Φ[tp] 180/π]], s["deg"], s[dp]},
{s[" θ lattd"], " = ", s[n0[Θ[tp] 180/π]], s["deg"], s[dp]},
{s[" d¹r/dτ¹"], " = ", s[n0[R'[tp]]], s["c"], s[dp]},
{s[" d¹φ/dτ¹"], " = ", s[n0[Φ'[tp]]], s["c\.b3/G/M"], s[dp]},
{s[" d¹θ/dτ¹"], " = ", s[n0[Θ'[tp]]], s["c\.b3/G/M"], s[dp]},
{s[" d\.b2r/dτ\.b2"], " = ", s[n0[R''[tp]]], s["c⁴/G/M"], s[dp]},
{s[" d\.b2φ/dτ\.b2"], " = ", s[n0[Φ''[tp]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" d\.b2θ/dτ\.b2"], " = ", s[n0[Θ''[tp]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" a SpinP"], " = ", s[n0[a]], s["GM²/c"], s[dp]},

{s[" Ř crc.φ"], " = ", s[n0[яi[tp]]], s["GM/c²"], s[dp]},
{s[" Σ crc.θ"], " = ", s[n0[Sqrt[Σi[tp]]]], s["GM/c²"], s[dp]},
{s[" M irred"], " = ", s[N[mirr]], s["M"], s[dp]},
{s[" E kinet"], " = ", s[n0[ekin[tp]]], s["mc²"], s[dp]},
{s[" E poten"], " = ", s[n0[epot[tp]]], s["mc²"], s[dp]},
{s[" E total"], " = ", s[n0[ε]], s["mc²"], s[dp]},
{s[" CarterQ"], " = ", s[n0[Q]], s["(GMm/c)²"], s[dp]},
{s[" L axial"], " = ", s[n0[Lz]], s["GMm/c"], s[dp]},
{s[" L polar"], " = ", s[n0[If[crd==1, pΘ[T], pΘks[T]]]], s["GMm/c"], s[dp]},
{s[" p r.mom"], " = ", s[n0[If[crd==1, pR[tp], pRks[tp]]]], s["mc"], s[dp]},

{s[" ω fdrag"], " = ", s[n0[ω[tp]]], s["c³/G/M"], s[dp]},
{s[" v fdrag"], " = ", s[n0[й[tp]]], s["c"], s[dp]},
{s[" Ω fdrag"], " = ", s[n0[Ω[tp]]], s["c"], s[dp]},
{s[" v propr"], " = ", s[n0[v[tp]/Sqrt[1-v[tp]^2]]], s["c"], s[dp]},
{s[" v escpe"], " = ", s[n0[ж[tp]]], s["c"], s[dp]},
{s[" v obsvd"], " = ", s[n0[ß[tp]]], s["c"], s[dp]},
{s[" v r,loc"], " = ", s[n0[vr[tp]]], s["c"], s[dp]},
{s[" v θ,loc"], " = ", s[n0[vθ[tp]]], s["c"], s[dp]},
{s[" v φ,loc"], " = ", s[n0[vφ[tp]]], s["c"], s[dp]},
{s[" v local"], " = ", s[n0[v[tp]]], s["c"], s[dp]},
{s[" "], s[" "], s["                       "], s["         "]}},
Alignment-> Left, Spacings-> {0, 0}];
 
plot1b[{xx_, yy_, zz_, tk_, w1_, w2_}] :=                                    (* Animation *)
Show[

Graphics3D[{
{PointSize[0.011], Red, Point[
Xyz[xyZ[{x[tp], y[tp], z[tp]}, w1], w2]]}},
ImageSize-> imgsize,
PlotRange-> {
{-(2 Sign[Abs[xx]]+1) PR, +(2 Sign[Abs[xx]]+1) PR},
{-(2 Sign[Abs[yy]]+1) PR, +(2 Sign[Abs[yy]]+1) PR},
{-(2 Sign[Abs[zz]]+1) PR, +(2 Sign[Abs[zz]]+1) PR}
},
SphericalRegion->False,
ImagePadding-> 1],

If[a==0,
Graphics3D[{Gray, Opacity[0.25], Sphere[{0,0,0}, 2]}],
horizons[A, None, w1, w2]],

If[A==0, {}, If[a==0, {}, ParametricPlot3D[
Xyz[xyZ[{
Sin[prm] a,
Cos[prm] a,
0}, w1], w2],
{prm, 0, 2π},
PlotStyle -> {Thickness[0.005], Orange}]]],

If[crd==1, If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ω0 т[tp]+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 т[tp]+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]],
If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ т[tp]+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ т[tp]+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]]],

If[crd==1, If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ω0 т[tt]+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 т[tt]+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, д[т[tp]-1/2 π/ω0]], tp},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> 12]]],
If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ т[tt]+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ т[tt]+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, д[т[tp]-1/2 π/ω0]], tp},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> 12]]]],

If[tk==0, {},
Block[{$RecursionLimit = Mrec},
ParametricPlot3D[
Xyz[xyZ[{x[tt], y[tt], z[tt]}, w1], w2], {tt, If[tp<0, Min[0, tp+d1], Max[0, tp-d1]], tp},
PlotStyle-> {Thickness[0.004]},
ColorFunction-> Function[{x, y, z, t},
Hue[0, 1, 0.5, If[tp<0, Max[Min[(+tp+(-t+d1))/d1, 1], 0], Max[Min[(-tp+(t+d1))/d1, 1], 0]]]],
ColorFunctionScaling-> False,
PlotPoints-> Automatic,
MaxRecursion-> mrec]]],

If[tk==0, {},
Block[{$RecursionLimit = Mrec},
ParametricPlot3D[
Xyz[xyZ[{x[tt], y[tt], z[tt]}, w1], w2], {tt, 0, If[tp<0, Min[-1*^-16, tp+d1/3], Max[1*^-16, tp-d1/3]]},
PlotStyle-> {Thickness[0.004], Opacity[0.6], Darker@Gray},
PlotPoints-> Plp,
MaxRecursion-> mrec]]],

ViewPoint-> {xx, yy, zz}];
 
Quiet[Do[
Print[Rasterize[Grid[{{
plot1b[{0, -Infinity, 0, tp, w1l, w2l}],
plot1b[{0, 0, +Infinity, tp, w1r, w2r}],
display[tp]
}, {"  ", "  ", "                                             "}
}, Alignment->Left]]],
{tp, 0, tMax, tMax/1}]]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 12) PLOT NACH KOORDINATENZEIT ||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
display[T_] := Grid[{
{s[" t coord"], " = ", s[n0[tk]], s["GM/c³"], s[dp]},
(* {s[" т coord"], " = ", s[n0[tk+Sign[1.5-dsp] 2 NIntegrate[R[Ti]/(R[Ti]^2-2 R[Ti]+a^2),{Ti,0,T}]]], s["GM/c³"], s[dp]}, *)
{If[μ==0, s[" affineP"], s[" τ propr"]], " = ", s[n0[T]], s["GM/c³"], s[dp]},
{s[" ṫ total"], " = ", s[n0[If[dsp==1, ю[T]-2 If[crd==1, 0, R'[T] R[T]/(R[T]^2-2 R[T]+a^2)], ю[T]]]], s[If[dsp==1, "dt/dτ", "dт/dτ"]], s[dp]},
{s[" ς gravt"], " = ", s[n0[ς[T]]], s["dt/dτ"], s[dp]},
{s[" γ kinet"], " = ", If[μ==0, s[n0[ς[T]]], s[n0[1/Sqrt[1-v[T]^2]]]], s["dt/dτ"], s[dp]},
{s[" R carts"], " = ", s[n0[XYZ[T]]], s["GM/c²"], s[dp]},
{s[" x carts"], " = ", s[n0[X[T]]], s["GM/c²"], s[dp]},
{s[" y carts"], " = ", s[n0[Y[T]]], s["GM/c²"], s[dp]},
{s[" z carts"], " = ", s[n0[Z[T]]], s["GM/c²"], s[dp]},
{s[" s dstnc"], " = ", s[n0[dst[T]]], s["GM/c²"], s[dp]},

{s[" r coord"], " = ", s[n0[R[T]]], s["GM/c²"], s[dp]},
{s[" φ longd"], " = ", s[n0[Φ[T] 180/π]], s["deg"], s[dp]},
{s[" θ lattd"], " = ", s[n0[Θ[T] 180/π]], s["deg"], s[dp]},
{s[" d¹r/dτ¹"], " = ", s[n0[R'[T]]], s["c"], s[dp]},
{s[" d¹φ/dτ¹"], " = ", s[n0[Φ'[T]]], s["c\.b3/G/M"], s[dp]},
{s[" d¹θ/dτ¹"], " = ", s[n0[Θ'[T]]], s["c\.b3/G/M"], s[dp]},
{s[" d\.b2r/dτ\.b2"], " = ", s[n0[R''[T]]], s["c⁴/G/M"], s[dp]},
{s[" d\.b2φ/dτ\.b2"], " = ", s[n0[Φ''[T]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" d\.b2θ/dτ\.b2"], " = ", s[n0[Θ''[T]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" a SpinP"], " = ", s[n0[a]], s["GM²/c"], s[dp]},

{s[" Ř crc.φ"], " = ", s[n0[яi[T]]], s["GM/c²"], s[dp]},
{s[" Σ crc.θ"], " = ", s[n0[Sqrt[Σi[T]]]], s["GM/c²"], s[dp]},
{s[" M irred"], " = ", s[N[mirr]], s["M"], s[dp]},
{s[" E kinet"], " = ", s[n0[ekin[T]]], s["mc²"], s[dp]},
{s[" E poten"], " = ", s[n0[epot[T]]], s["mc²"], s[dp]},
{s[" E total"], " = ", s[n0[ε]], s["mc²"], s[dp]},
{s[" CarterQ"], " = ", s[n0[Q]], s["(GMm/c)²"], s[dp]},
{s[" L axial"], " = ", s[n0[Lz]], s["GMm/c"], s[dp]},
{s[" L polar"], " = ", s[n0[If[crd==1, pΘ[T], pΘks[T]]]], s["GMm/c"], s[dp]},
{s[" p r.mom"], " = ", s[n0[If[crd==1, pR[T], pRks[T]]]], s["mc"], s[dp]},

{s[" ω fdrag"], " = ", s[n0[Abs[ω[T]]]], s["c³/G/M"], s[dp]},
{s[" v fdrag"], " = ", s[n0[Abs[й[T]]]], s["c"], s[dp]},
{s[" Ω fdrag"], " = ", s[n0[Abs[Ω[T]]]], s["c"], s[dp]},
{s[" v propr"], " = ", s[n0[v[T]/Sqrt[1-v[T]^2]]], s["c"], s[dp]},
{s[" v escpe"], " = ", s[n0[ж[T]]], s["c"], s[dp]},
{s[" v obsvd"], " = ", s[n0[ß[T]]], s["c"], s[dp]},
{s[" v r,loc"], " = ", s[n0[vr[T]]], s["c"], s[dp]},
{s[" v θ,loc"], " = ", s[n0[vθ[T]]], s["c"], s[dp]},
{s[" v φ,loc"], " = ", s[n0[vφ[T]]], s["c"], s[dp]},
{s[" v local"], " = ", s[n0[v[T]]], s["c"], s[dp]},
{s[" "], s[" "], s["                       "], s["         "]}},
Alignment-> Left, Spacings-> {0, 0}];
 
plot1a[{xx_, yy_, zz_, tk_, w1_, w2_}]:=                                     (* Animation *)
Show[

Graphics3D[{
{PointSize[0.011], Red, Point[
Xyz[xyZ[{x[T], y[T], z[T]}, w1], w2]]}},
ImageSize-> imgsize,
PlotRange-> {
{-(2 Sign[Abs[xx]]+1) PR, +(2 Sign[Abs[xx]]+1) PR},
{-(2 Sign[Abs[yy]]+1) PR, +(2 Sign[Abs[yy]]+1) PR},
{-(2 Sign[Abs[zz]]+1) PR, +(2 Sign[Abs[zz]]+1) PR}
},
SphericalRegion->False,
ImagePadding-> 1],

If[a==0,
Graphics3D[{Gray, Opacity[0.25], Sphere[{0,0,0}, 2]}],
horizons[A, None, w1, w2]],

If[A==0, {}, If[a==0, {}, ParametricPlot3D[
Xyz[xyZ[{
Sin[prm] a,
Cos[prm] a,
0}, w1], w2],
{prm, 0, 2π},
PlotStyle -> {Thickness[0.005], Orange}]]],

If[crd==1, If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ω0 tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]],
If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]]],

If[crd==1, If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ω0 tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, tk-1/2 π/ω0], tk},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> mrec]]],
If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, tk-1/2 π/ω0], tk},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> mrec]]]],

Block[{$RecursionLimit = Mrec},
If[tk==0, {},
ParametricPlot3D[
Xyz[xyZ[{x[tt], y[tt], z[tt]}, w1], w2], {tt, If[TMax<0, Min[0, T+d1], Max[0, T-d1]], T},
PlotStyle-> {Thickness[0.004]},
ColorFunction-> Function[{x, y, z, t},
Hue[0, 1, 0.5, If[TMax<0, Max[Min[(+T+(-t+d1))/d1, 1], 0], Max[Min[(-T+(t+d1))/d1, 1], 0]]]],
ColorFunctionScaling-> False,
PlotPoints-> Automatic,
MaxRecursion-> mrec]]],

If[tk==0, {},
Block[{$RecursionLimit = Mrec},
ParametricPlot3D[
Xyz[xyZ[{x[tt], y[tt], z[tt]}, w1], w2], {tt, 0, If[Tmax<0, Min[-1*^-16, T+d1/3], Max[1*^-16, T-d1/3]]},
PlotStyle-> {Thickness[0.004], Opacity[0.6], Darker@Gray},
PlotPoints-> Plp,
MaxRecursion-> mrec]]],

ViewPoint-> {xx, yy, zz}];
 
Quiet[Do[
Print[Rasterize[Grid[{{
plot1a[{0, -Infinity, 0, tk, w1l, w2l}],
plot1a[{0, 0, Infinity, tk, w1r, w2r}],
display[Quiet[д[tk]]]
}, {"  ", "  ", "                                             "}
}, Alignment->Left]]],
{tk, 0, TMax, TMax/1}]]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 13) EXPORTOPTIONEN |||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
(* Export als HTML Dokument *)
(* Export["Y:\\export\\dateiname.html", EvaluationNotebook[], "GraphicsOutput" -> "PNG"]  *)
(* Export direkt als Bildsequenz *)
(* Do[Export["Y:\\export\\dateiname" <> ToString[tk] <> ".png", Rasterize[...]            *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||| http://kerr.yukerez.net ||||| Simon Tyran, Vienna ||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)















#2 Interpolationsfunktion für den schnelleren Output vieler Einzelbilder bei dafür etwas längerer Anlaufzeit:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||| 11) PLOT NACH KOORDINATENZEIT ||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

Plp=Round[Max[4, 2tk]];

rint=Evaluate[Interpolation[Table[{tint,R[д[tint]]},{tint,0,TMax,1/2}]]];
uint=Evaluate[Interpolation[Table[{tint,Θ[д[tint]]},{tint,0,TMax,1/2}]]];
pint=Evaluate[Interpolation[Table[{tint,Φ[д[tint]]},{tint,0,TMax,1/2}]]];
zint[τ_]:=rint[τ] Cos[uint[τ]];
xint[τ_]:=Sqrt[rint[τ]^2+a^2] Sin[uint[τ]] Cos[pint[τ]];
yint[τ_]:=Sqrt[rint[τ]^2+a^2] Sin[uint[τ]] Sin[pint[τ]];

display[T_]:=Grid[{
{s[" t coord"], " = ", s[n0[tk]], s["GM/c³"], s[dp]},
{If[μ==0, s[" affineP"], s[" τ propr"]], " = ", s[n0[T]], s["GM/c³"], s[dp]},
{s[" ṫ total"], " = ", s[n0[ю[T]]], s["dt/dτ"], s[dp]},
{s[" ς gravt"], " = ", s[n0[ς[T]]], s["dt/dτ"], s[dp]},
{s[" γ kinet"], " = ", If[μ==0, s[n0[ς[T]]], s[n0[1/Sqrt[1-v[T]^2]]]], s["dt/dτ"], s[dp]},
{s[" R carts"], " = ", s[n0[Sqrt[xint[tk]^2+yint[tk]^2+zint[tk]^2]]], s["GM/c²"], s[dp]},
{s[" x carts"], " = ", s[n0[xint[tk]]], s["GM/c²"], s[dp]},
{s[" y carts"], " = ", s[n0[yint[tk]]], s["GM/c²"], s[dp]},
{s[" z carts"], " = ", s[n0[zint[tk]]], s["GM/c²"], s[dp]},
{s[" s dstnc"], " = ", s[n0[dst[T]]], s["GM/c²"], s[dp]},

{s[" r coord"], " = ", s[n0[rint[tk]]], s["GM/c²"], s[dp]},
{s[" φ longd"], " = ", s[n0[pint[tk] 180/π]], s["deg"], s[dp]},
{s[" θ lattd"], " = ", s[n0[uint[tk] 180/π]], s["deg"], s[dp]},
{s[" d¹r/dτ¹"], " = ", s[n0[R'[T]]], s["c"], s[dp]},
{s[" d¹φ/dτ¹"], " = ", s[n0[Φ'[T]]], s["c\.b3/G/M"], s[dp]},
{s[" d¹θ/dτ¹"], " = ", s[n0[Θ'[T]]], s["c\.b3/G/M"], s[dp]},
{s[" d\.b2r/dτ\.b2"], " = ", s[n0[R''[T]]], s["c⁴/G/M"], s[dp]},
{s[" d\.b2φ/dτ\.b2"], " = ", s[n0[Φ''[T]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" d\.b2θ/dτ\.b2"], " = ", s[n0[Θ''[T]]], s["c⁶/G\.b2/M\.b2"], s[dp]},
{s[" a SpinP"], " = ", s[n0[a]], s["GM²/c"], s[dp]},

{s[" Ř crc.φ"], " = ", s[n0[яi[T]]], s["GM/c²"], s[dp]},
{s[" Σ crc.θ"], " = ", s[n0[Sqrt[Σi[T]]]], s["GM/c²"], s[dp]},
{s[" M irred"], " = ", s[N[mirr]], s["M"], s[dp]},
{s[" E kinet"], " = ", s[n0[ekin[T]]], s["mc²"], s[dp]},
{s[" E poten"], " = ", s[n0[epot[T]]], s["mc²"], s[dp]},
{s[" E total"], " = ", s[n0[ε]], s["mc²"], s[dp]},
{s[" CarterQ"], " = ", s[n0[Q]], s["(GMm/c)²"], s[dp]},
{s[" L axial"], " = ", s[n0[Lz]], s["GMm/c"], s[dp]},
{s[" L polar"], " = ", s[n0[If[crd==1, pΘ[T], pΘks[T]]]], s["GMm/c"], s[dp]},
{s[" p r.mom"], " = ", s[n0[If[crd==1, pR[T], pRks[T]]]], s["mc"], s[dp]},

{s[" ω fdrag"], " = ", s[n0[Abs[ω[T]]]], s["c³/G/M"], s[dp]},
{s[" v fdrag"], " = ", s[n0[Abs[й[T]]]], s["c"], s[dp]},
{s[" Ω fdrag"], " = ", s[n0[Abs[Ω[T]]]], s["c"], s[dp]},
{s[" v propr"], " = ", s[n0[v[T]/Sqrt[1-v[T]^2]]], s["c"], s[dp]},
{s[" v escpe"], " = ", s[n0[ж[T]]], s["c"], s[dp]},
{s[" v obsvd"], " = ", s[n0[ß[T]]], s["c"], s[dp]},
{s[" v r,loc"], " = ", s[n0[vr[T]]], s["c"], s[dp]},
{s[" v θ,loc"], " = ", s[n0[vθ[T]]], s["c"], s[dp]},
{s[" v φ,loc"], " = ", s[n0[vφ[T]]], s["c"], s[dp]},
{s[" v local"], " = ", s[n0[v[T]]], s["c"], s[dp]},
{s[" "], s[" "], s["                       "], s["         "]}},
Alignment-> Left, Spacings-> {0, 0}];

hz=If[a==0,
Graphics3D[{Gray, Opacity[0.25], Sphere[{0,0,0}, 2]}],
horizons[A, None, w1, w2]];
 
plot1a[{xx_, yy_, zz_, tk_, w1_, w2_}]:=                                     (* Animation *)
Show[

Graphics3D[{
{PointSize[0.011], Red, Point[
Xyz[xyZ[{xint[tk], yint[tk], zint[tk]}, w1], w2]]}},
ImageSize-> imgsize,
PlotRange-> {
{-(2 Sign[Abs[xx]]+1) PR, +(2 Sign[Abs[xx]]+1) PR},
{-(2 Sign[Abs[yy]]+1) PR, +(2 Sign[Abs[yy]]+1) PR},
{-(2 Sign[Abs[zz]]+1) PR, +(2 Sign[Abs[zz]]+1) PR}
},
SphericalRegion->False,
ImagePadding-> 1],

horizons[A, None, w1, w2],

If[A==0, {}, If[a==0, {}, ParametricPlot3D[
Xyz[xyZ[{
Sin[prm] a,
Cos[prm] a,
0}, w1], w2],
{prm, 0, 2π},
PlotStyle -> {Thickness[0.005], Orange}]]],

If[crd==1, If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ω0 tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]],
If[a==0, {},
Graphics3D[{{PointSize[0.009], Purple, Point[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ tk+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2]]}}]]],

If[crd==1, If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ω0 tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ω0 tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, tk-199/100 π/ω0], tk},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> mrec]]],
If[tk==0, {}, If[a==0, {},
ParametricPlot3D[
Xyz[xyZ[{
Sin[-φ0-ц0 a Ξ/χ tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
Cos[-φ0-ц0 a Ξ/χ tt+π/2] Sqrt[x0[A]^2+y0[A]^2],
z0[A]}, w1], w2],
{tt, Max[0, tk-199/100 π/ω0], tk},
PlotStyle -> {Thickness[0.001], Dashed, Purple},
PlotPoints-> Automatic,
MaxRecursion-> mrec]]]],

Block[{$RecursionLimit = Mrec},
If[tk==0, {},
ParametricPlot3D[
Xyz[xyZ[{xint[tt], yint[tt], zint[tt]}, w1], w2], {tt, If[TMax<0, Min[0, tk+d1], Max[0, tk-d1]], tk},
PlotStyle-> {Thickness[0.004]},
ColorFunction-> Function[{x, y, z, t},
Hue[0, 1, 0.5, If[TMax<0, Max[Min[(+tk+(-t+d1))/d1, 1], 0], Max[Min[(-tk+(t+d1))/d1, 1], 0]]]],
ColorFunctionScaling-> False,
PlotPoints-> Automatic,
MaxRecursion-> mrec]]],

If[tk==0, {},
Block[{$RecursionLimit = Mrec},
ParametricPlot3D[
Xyz[xyZ[{xint[tt], yint[tt], zint[tt]}, w1], w2],
{tt, 0, If[Tmax<0, Min[-1*^-16, tk+d1/3], Max[1*^-16, tk-d1/3]]},
PlotStyle-> {Thickness[0.004], Opacity[0.6], Darker@Gray},
PlotPoints-> Plp,
MaxRecursion-> mrec]]],

ViewPoint-> {xx, yy, zz}];
 
Quiet[Do[
Print[Rasterize[Grid[{{
plot1a[{0, -Infinity, 0, tk, w1l, w2l}],
plot1a[{0, 0, Infinity, tk, w1r, w2r}],
display[Quiet[д[tk]]]
}, {"  ", "  ", "                                             "}
}, Alignment->Left]]],
{tk, 0, TMax, TMax/1}]]















#3 Erhaltungsgrößen Testmonitor zur Kontrolle der numerischen Stabilität:

Code: Alles auswählen

N@ε

ε0=With[{τ=0},Evaluate[+((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]]]

ε1=With[{τ=tMax 99/100},Evaluate[+((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]]]

N@Lz

Lz0=With[{τ=0},Evaluate[(q a r[τ] 0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]]]

Lz1=With[{τ=tMax 99/100},Evaluate[(q a r[τ]0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]]]

N@Q

Q0=With[{τ=0},Evaluate[((θ'[τ] (r[τ]^2+a^2 Cos[θ[τ]]^2))^2+(((q a r[τ]0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2 Csc[θ[τ]]^2-a^2 ((((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2+μ)) Cos[θ[τ]]^2)/.sol][[1]]]

Q1=With[{τ=tMax 99/100},Evaluate[((θ'[τ] (r[τ]^2+a^2 Cos[θ[τ]]^2))^2+(((q a r[τ]0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2 Csc[θ[τ]]^2-a^2 ((((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2+μ)) Cos[θ[τ]]^2)/.sol][[1]]]

Plot[{
Evaluate[+((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]],
Evaluate[(q a r[τ]0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2)/.sol][[1]],
Evaluate[((θ'[τ] (r[τ]^2+a^2 Cos[θ[τ]]^2))^2+(((q a r[τ]0 Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)-(a t'[τ]  (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2)+(φ'[τ] Sin[θ[τ]]^2 ((a^2+r[τ]^2)^2-a^2 (a^2-2 r[τ]+r[τ]^2+0^2) Sin[θ[τ]]^2))/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2 Csc[θ[τ]]^2-a^2 ((((q r[τ] 0)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+t'[τ] (1-(2 r[τ]-0^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))+(a φ'[τ] (2 r[τ]-0^2) Sin[θ[τ]]^2)/(r[τ]^2+a^2 Cos[θ[τ]]^2))^2+μ)) Cos[θ[τ]]^2)/.sol][[1]]
}, {τ, 0, tMax 99/100}, PlotPoints->100, ImageSize->300, Frame->True]















#4 Solver für die Startbedingungen; Umrechung von lokaler Geschwindigkeit, Eigenzeitableitungen und Erhaltungsgrößen:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || CODE 1: Lokale Geschwindigkeit nach Erhaltungsgrößen ε, Lz, Q ||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ClearAll["Local`*"];
 
(* || Startposition etc. eingeben  |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 7;
θ0 = π/2;
φ0 = 0;
a  = 9/10;
μ  =-1;
 
(* || Erhaltungsgrößen Gesamtenergie, axialer Drehimpuls & Carter Konstante eingeben |||| *)
 
ε  = (72 Sqrt[3/2136769])/7+5 Sqrt[3581/105087];
Lz = (2 Sqrt[105087/61])/35;
Q  = 700/183;
 
(* || Gleichungen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ε0 = (Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))/Sqrt[1+μ v0^2];
L0 = (vφ0 Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)])/Sqrt[1+μ v0^2];
Q0 = (vθ0^2 (r0^2+a^2 Cos[θ0]^2)+(vφ0^2 Cos[θ0]^2 ((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))/(r0^2+a^2 Cos[θ0]^2)-a^2 Cos[θ0]^2 (-1+v0^2+(Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))^2))/(1+μ v0^2);
 
(* || Output: lokale Geschwindigkeitskomponenten  ||||||||||||||||||||||||||||||||||||||| *)
 
"Code 1"
FindInstance[ε0==ε && L0==Lz && Q0==Q && vr0^2==v0^2-vφ0^2-vθ0^2 && v0>0 && vθ0>=0, {v0,vr0,vφ0,vθ0}, Reals]
N[%]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| Mathematica Syntax |||| http://kerr.yukterez.net |||| Simon Tyran, Vienna  ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
(* || *)
    (* || *)
        (* || *)
            (* || *)
                 (* || *)
                      (* || *)
                          (* || *)
                              (* || *)
                                  (* ||*)
                                      (* || *)
                                          (* || *)
                                              (* || *)
                                                   (* || *)
                                                        (* || *)
                                                            (* || *)
                                                                (* || *)
                                                                    (* || *)
                                                                        (* ||*)
                                                                            (* || *)
                                                                                (* || *)
                                                                                    (* || *)
                                                                                   
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || CODE 2: Lokale Geschwindigkeit nach ersten Eigenzeitableitungen  |||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ClearAll["Local`*"];
 
(* || Startposition etc. eingeben  |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 7;
θ0 = π/2;
φ0 = 0;
a  = 9/10;
μ  =-1;
 
(* || Startwerte für die ersten Eigenzeitableitungen eingeben ||||||||||||||||||||||||||| *)
 
dt = (5 Sqrt[35029/10743])/7;
dr = 0;
dθ = 10/(7 Sqrt[1281]);
dφ = (300 Sqrt[3/125438849])/7+40 Sqrt[3/2136769];
 
(* || Gleichungen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ε0 = (Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))/Sqrt[1+μ v0^2];
L0 = (vφ0 Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)])/Sqrt[1+μ v0^2];
Q0 = (vθ0^2 (r0^2+a^2 Cos[θ0]^2)+(vφ0^2 Cos[θ0]^2 ((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))/(r0^2+a^2 Cos[θ0]^2)-a^2 Cos[θ0]^2 (-1+v0^2+(Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))^2))/(1+μ v0^2);
 
Ξ=r0^2+a^2 Cos[θ0]^2;
δ=r0^2-2r0+a^2;
j[v_]:=Sqrt[1+μ v^2];
pr0=vr0 Sqrt[(Ξ/δ)/j[v0]^2];
pθ0=vθ0 Sqrt[Ξ]/j[v0];
 
dT=ε0+(2r0(r0^2+a^2)ε0-2 a r0 L0)/(Ξ δ);
dR=(pr0 δ)/Ξ;
dΘ=pθ0/Ξ;
dΦ=(2 a r0 ε0+(Ξ-2 r0)L0 Csc[θ0]^2)/(Ξ δ);
 
(* || Output: lokale Geschwindigkeitskomponenten  ||||||||||||||||||||||||||||||||||||||| *)
 
"Code 2"
FindInstance[dT==dt && dR==dr && dΘ==dθ && dΦ==dφ && v0>0, {v0,vr0,vφ0,vθ0}, Reals]
N[%]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| Mathematica Syntax |||| http://kerr.yukterez.net |||| Simon Tyran, Vienna  ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
(* || *)
    (* || *)
        (* || *)
            (* || *)
                 (* || *)
                      (* || *)
                          (* || *)
                              (* || *)
                                  (* ||*)
                                      (* || *)
                                          (* || *)
                                              (* || *)
                                                   (* || *)
                                                        (* || *)
                                                            (* || *)
                                                                (* || *)
                                                                    (* || *)
                                                                        (* ||*)
                                                                            (* || *)
                                                                                (* || *)
                                                                                    (* || *)
                                                                                                                                                               
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || CODE 3: Erste Eigenzeitableitungen nach lokalen Geschwindigkeiten ||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ClearAll["Local`*"];
 
(* || Startposition etc. eingeben  |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 7;
θ0 = π/2;
φ0 = 0;
a  = 9/10;
μ  =-1;
 
(* || Startwerte für die ersten Eigenzeitableitungen eingeben ||||||||||||||||||||||||||| *)
 
vr0 = 0;
vθ0 = 2/Sqrt[61];
vφ0 = 12/(5 Sqrt[61]);
v0  = Sqrt[vr0^2+vθ0^2+vφ0^2];
 
(* || Gleichungen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ε0 = (Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))/Sqrt[1+μ v0^2];
L0 = (vφ0 Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)])/Sqrt[1+μ v0^2];
Q0 = (vθ0^2 (r0^2+a^2 Cos[θ0]^2)+(vφ0^2 Cos[θ0]^2 ((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))/(r0^2+a^2 Cos[θ0]^2)-a^2 Cos[θ0]^2 (-1+v0^2+(Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))^2))/(1+μ v0^2);
 
Ξ=r0^2+a^2 Cos[θ0]^2;
δ=r0^2-2r0+a^2;
j[v_]:=Sqrt[1+μ v^2];
pr0=vr0 Sqrt[(Ξ/δ)/j[v0]^2];
pθ0=vθ0 Sqrt[Ξ]/j[v0];
 
dT=ε0+(2r0(r0^2+a^2)ε0-2 a r0 L0)/(Ξ δ);
dR=(pr0 δ)/Ξ;
dΘ=pθ0/Ξ;
dΦ=(2 a r0 ε0+(Ξ-2 r0)L0 Csc[θ0]^2)/(Ξ δ);
 
(* || Output: lokale Geschwindigkeitskomponenten  ||||||||||||||||||||||||||||||||||||||| *)
 
"Code 3"
FindInstance[dT==dt && dR==dr && dΘ==dθ && dΦ==dφ, {dt,dr,dθ,dφ}, Reals]
N[%]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| Mathematica Syntax |||| http://kerr.yukterez.net |||| Simon Tyran, Vienna  ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
(* || *)
    (* || *)
        (* || *)
            (* || *)
                 (* || *)
                      (* || *)
                          (* || *)
                              (* || *)
                                  (* ||*)
                                      (* || *)
                                          (* || *)
                                              (* || *)
                                                   (* || *)
                                                        (* || *)
                                                            (* || *)
                                                                (* || *)
                                                                    (* || *)
                                                                        (* ||*)
                                                                            (* || *)
                                                                                (* || *)
                                                                                    (* || *)
                                                                                   
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || CODE 4: Erhaltungsgrößen ε, Lz, Q nach lokalen Geschwindigkeiten |||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ClearAll["Local`*"];
 
(* || Startposition etc. eingeben  |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 7;
θ0 = π/2;
φ0 = 0;
a  = 9/10;
μ  =-1;
 
(* || Startwerte für die ersten Eigenzeitableitungen eingeben ||||||||||||||||||||||||||| *)
 
vr0 = 0;
vθ0 = 2/Sqrt[61];
vφ0 = 12/(5 Sqrt[61]);
v0  = Sqrt[vr0^2+vθ0^2+vφ0^2];
 
(* || Gleichungen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ε0 = (Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))/Sqrt[1+μ v0^2];
L0 = (vφ0 Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)])/Sqrt[1+μ v0^2];
Q0 = (vθ0^2 (r0^2+a^2 Cos[θ0]^2)+(vφ0^2 Cos[θ0]^2 ((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2))/(r0^2+a^2 Cos[θ0]^2)-a^2 Cos[θ0]^2 (-1+v0^2+(Sqrt[((a^2+(-2+r0) r0) (r0^2+a^2 Cos[θ0]^2))/((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)]+(2 a r0 vφ0 Sin[θ0])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2+(-2+r0) r0) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]))^2))/(1+μ v0^2);
 
Ξ=r0^2+a^2 Cos[θ0]^2;
δ=r0^2-2r0+a^2;
j[v_]:=Sqrt[1+μ v^2];
pr0=vr0 Sqrt[(Ξ/δ)/j[v0]^2];
pθ0=vθ0 Sqrt[Ξ]/j[v0];
 
dT=ε0+(2r0(r0^2+a^2)ε0-2 a r0 L0)/(Ξ δ);
dR=(pr0 δ)/Ξ;
dΘ=pθ0/Ξ;
dΦ=(2 a r0 ε0+(Ξ-2 r0)L0 Csc[θ0]^2)/(Ξ δ);
 
(* || Output: lokale Geschwindigkeitskomponenten  ||||||||||||||||||||||||||||||||||||||| *)
 
"Code 4"
FindInstance[ε==ε0 && Lz==L0 && Q==Q0, {ε,Lz,Q}, Reals]
N[%]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| Mathematica Syntax |||| http://kerr.yukterez.net |||| Simon Tyran, Vienna  ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

(* || *)
    (* || *)
        (* || *)
            (* || *)
                 (* || *)
                      (* || *)
                          (* || *)
                              (* || *)
                                  (* ||*)
                                      (* || *)
                                          (* || *)
                                              (* || *)
                                                   (* || *)
                                                        (* || *)
                                                            (* || *)
                                                                (* || *)
                                                                    (* || *)
                                                                        (* ||*)
                                                                            (* || *)
                                                                                (* || *)
                                                                                    (* || *)
                                                               
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || CODE 5: Erste Eigenzeitableitungen nach Erhaltungsgrößen ε, Lz, Q ||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ClearAll["Local`*"];
 
(* || Startposition etc. eingeben  |||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 7;
θ0 = π/2;
φ0 = 0;
a  = 9/10;
μ  =-1;
 
(* || Erhaltungsgrößen Gesamtenergie, axialer Drehimpuls & Carter Konstante eingeben |||| *)
 
ε = (216 Sqrt[14957383]+2135 Sqrt[878071943])/(14957383 Sqrt[21]);
Lz = (2 Sqrt[105087/61])/35;
Q = 700/183;
 
(* || Gleichungen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

℧  = 0;
q  = 0;
 
Ξ=r0^2+a^2 Cos[θ0]^2;
δ=r0^2-2r0+a^2+℧^2;
χ=(r0^2+a^2)^2-a^2 Sin[θ0]^2 δ;
Xj=a Sin[θ0]^2;
щ=(q ℧ r0 (a^2+r0^2))/(δ Ξ);

gtt=1-(2 r0-℧^2)/Ξ;
grr=-Ξ/δ;
gθθ=-Ξ;
gφφ=-χ/Ξ Sin[θ0]^2;
gtφ=a (2r0-℧^2) Sin[θ0]^2/Ξ;

P=ε(r0^2+a^2)+℧ q r0-a Lz;
Vr=P^2-δ(μ^2 r0^2+(Lz-a ε)^2+Q);
Vθ=Q-Cos[θ0]^2(a^2(μ^2-ε^2)+Lz^2/Sin[θ0]^2);

dT=Abs[1/(δ Ξ Sin[θ0]^2) (Lz (δ Xj-a Sin[θ0]^2 (r0^2+a^2))+ε (-δ Xj^2+Sin[θ0]^2 (r0^2+a^2)^2)-q ℧ r0 Sin[θ0]^2 (r0^2+a^2))];
dR=Sqrt[Abs[Vr]]/Ξ;
dΘ=Sqrt[Abs[Vθ]]/Ξ;
dΦ=1/(δ Ξ Sin[θ0]^2) (ε (-δ Xj+a Sin[θ0]^2 (r0^2+a^2))+Lz (δ-a^2 Sin[θ0]^2)-q ℧ r0 a Sin[θ0]^2);

(* || Output: lokale Geschwindigkeitskomponenten  ||||||||||||||||||||||||||||||||||||||| *)
 
"Code 5"
Simplify[FindInstance[{dt==dT && dr==dR && dθ==dΘ && dφ==dΦ}, {dt, dr, dθ, dφ}]]
N[%]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| Mathematica Syntax |||| kerr.newman.yukterez.net |||| Simon Tyran, Vienna  ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)















#5 Geodätische Gleichung, Boyer-Lindquist:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* | Mathematica Syntax | GEODESIC SOLVER | geodesics.yukterez.net | Version 23.12.2019 | *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

ClearAll["Global`*"]
                                               (* Input: kovariante metrische Komponenten *)
g11=gtt=1-(2r-℧^2)/Σ;
g22=grr=-Σ/Δ;
g33=gθθ=-Σ;
g44=gφφ=-Χ/Σ Sin[θ]^2;
g14=gtφ=a (2r-℧^2) Sin[θ]^2/Σ;
g12=g13=g23=g24=g34=0;
                                                                           (* Abkürzungen *)
Σ=r^2+a^2 Cos[θ]^2;
Δ=r^2-2 r+a^2+℧^2;
Χ=(r^2+a^2)^2-a^2 Sin[θ]^2 Δ;
щ=(q ℧ r (a^2+r^2))/(Δ Σ);
              (* Koordinaten, Dimensionen, magnetisches Monopol, elektrische Ladung, Spin *)
x={t, r, θ, φ}; n=4; P=0; Ω=℧; ℧=℧; a=a;
                                                                         "Metrischer Tensor"
mt={{g11, g12, g13, g14}, {g12, g22, g23, g24}, {g13, g23, g33, g34}, {g14, g24, g34, g44}};
Subscript["g", μσ] -> MatrixForm[mt]
it=Simplify[Inverse[mt]];
"g"^μσ -> MatrixForm[it]
                                                                            "Maxwell Tensor"
A={0, 0, 0, 0};
F=Simplify[Table[((D[A[[j]], x[[k]]]-D[A[[k]], x[[j]]])), {j, 1, n}, {k, 1, n}], Reals];
Subscript["F", μσ] -> MatrixForm[F]
f=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] F[[k, l]],
{k, 1, n}, {l, 1, n}], {i, 1, n}, {j, 1, n}], Reals];
"F"^μσ -> MatrixForm[f]
                                                                        "Christoffelsymbole"
chr=Simplify[Table[(1/2)Sum[(it[[i, s]])
(D[mt[[s, j]], x[[k]]]+D[mt[[s, k]], x[[j]]] -D[mt[[j, k]], x[[s]]]), {s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}]];
crs=Table[If[UnsameQ[chr[[i, j, k]], 0],
{ToString[Γ[i, j, k]], chr[[i, j, k]]}], {i, 1, n}, {j, 1, n}, {k, 1, j}];
TableForm[Partition[DeleteCases[Flatten[crs], Null], 2]]                   
                                                                            "Riemann Tensor"
rmn=Simplify[Table[
D[chr[[i, j, l]], x[[k]]] - D[chr[[i, j, k]], x[[l]]] +
Sum[chr[[s, j, l]] chr[[i, k, s]] -
chr[[s, j, k]] chr[[i, l, s]],
{s, 1, n}], {i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
rie=Table[If[UnsameQ[rmn[[i, j, k, l]], 0],
{ToString[R[i, j, k, l]], rmn[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, k - 1}];
TableForm[Partition[DeleteCases[Flatten[rie], Null], 2]]
                                                                              "Ricci Tensor"
rcc=Simplify[Table[
Sum[rmn[[i, j, i, l]], {i, 1, n}], {j, 1, n}, {l, 1, n}]];
Subscript["Ř", μσ] -> MatrixForm[rcc]
ric=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] rcc[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"Ř"^μσ -> MatrixForm[ric]
                                                                              "Ricci Skalar"
Ř=Simplify[Sum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ř"->Ř
                                                            (* kovarianter Riemann Tensor *)
rcv=Table[Sum[mt[[i, j]] rmn[[j, k, l, m]], {j, 1, 4}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
                                                        (* kontravarianter Riemann Tensor *)
rcn=Table[Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] rcv[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, 4}, {h, 1, n}, {o, 1, n}, {p, 1, n}];
                                                                        "Kretschmann Skalar"
krn= Sum[rcv[[i, j, k, l]] rcn[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
"K"->FullSimplify[krn]
                                                                           "Einstein Tensor"
est=Simplify[rcc-Ř mt/2];
Subscript["G", μσ] -> MatrixForm[est]
ein=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] est[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"G"^μσ -> MatrixForm[Simplify[ein]]

rplc[y_]:=(((((((y/.t->t[τ])/.r->r[τ])/.θ->θ[τ])/.φ->φ[τ])/.Derivative[1][t[τ]]->
t'[τ])/.Derivative[1][r[τ]]->r'[τ])/.Derivative[1][θ[τ]]->θ'[τ])/.Derivative[1][φ[τ]]->φ'[τ];
list[y_]:=y[[1]]==y[[2]];
                                                                      "Bewegungsgleichungen"
geo=Simplify[Table[-Sum[
chr[[i, j, k]] x[[j]]' x[[k]]'+q f[[i, k]] x[[j]]' mt[[j, k]],
{j, 1, n}, {k, 1, n}], {i, 1, n}]];

equ=Table[{x[[i]]''[τ]==Simplify[rplc[geo[[i]]], Reals]}, {i, 1, n}];

geodesic1=equ[[1]][[1]]
geodesic2=equ[[2]][[1]]
geodesic3=equ[[3]][[1]]
geodesic4=equ[[4]][[1]]
                                                                     "totale Zeitdilatation"
H=Sum[mt[[μ, ν]] x[[μ]]' x[[ν]]', {μ, 1, n}, {ν, 1, n}];                        
ṫ=Table[Quiet[rplc[Simplify[Normal[Solve[
-μ==(H/.t'->ť), ť]]][[j, 1, 2]]]], {j, 1, 2}];                        
Derivative[1][t][τ]->ṫ[[1]] || ṫ[[2]]
                                                                  "kovarianter Viererimpuls"
p[μ_]:=-(Sum[mt[[μ, ν]]*x[[ν]]', {ν, 1, n}]+q A[[μ]]);
pt[τ]->rplc[Simplify[p[1], Reals]]
pr[τ]->rplc[Simplify[p[2], Reals]]
pθ[τ]->rplc[Simplify[p[3], Reals]]
pφ[τ]->rplc[Simplify[p[4], Reals]]
                                                                    "lokale Geschwindigkeit"
V[x_]:=Simplify[Normal[Solve[vx Sqrt[-mt[[x, x]]]/Sqrt[1-μ^2 v[τ]^2]-(1-μ^2 v^2) q A[[x]]==
p[x], vx]][[1, 1]], Reals];                                                   
rplc[V[2]]/.vx->vr[τ]
rplc[V[3]]/.vx->vθ[τ]
rplc[V[4]]/.vx->vφ[τ]













#6 Geodätische Gleichung, Doran:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* | Mathematica Syntax | GEODESIC SOLVER | geodesics.yukterez.net | Version 23.12.2019 | *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

ClearAll["Global`*"]
                                               (* Input: kovariante metrische Komponenten *)
g11=gtt=1-(2 r)/Σ;
g12=gtr=-(( Sqrt[2] Sqrt[r (a^2+r^2)])/(a^2+r^2));
g13=gtθ=0;
g14=gtφ=(2 a r Sin[θ]^2)/Σ;
g22=grr=-(Σ/(a^2+r^2));
g23=grθ=0;
g24=grφ=( Sqrt[2] a  Sqrt[r (a^2+r^2)] Sin[θ]^2)/(a^2+r^2);
g33=gθθ=-Σ;
g34=gθφ=0;
g44=gφφ=-(r^2+a^2)Sin[θ]^2-(2 a^2 r Sin[θ]^4)/Σ;
                                                                           (* Abkürzungen *)
Σ=r^2+a^2 Cos[θ]^2;
Δ=r^2-2 r+a^2;
χ=(r^2+a^2)^2-a^2 Sin[θ]^2 Δ;
ц=2r/Σ;
              (* Koordinaten, Dimensionen, magnetisches Monopol, elektrische Ladung, Spin *)
x={t, r, θ, φ}; n=4; P=0; Ω=℧; ℧=℧; a=a;
                                                                         "Metrischer Tensor"
mt={{g11, g12, g13, g14}, {g12, g22, g23, g24}, {g13, g23, g33, g34}, {g14, g24, g34, g44}};
Subscript["g", μσ] -> MatrixForm[mt]
it=Simplify[Inverse[mt]];
"g"^μσ -> MatrixForm[it]
                                                                            "Maxwell Tensor"
A={0, 0, 0, 0};
F=Simplify[Table[((D[A[[j]], x[[k]]]-D[A[[k]], x[[j]]])), {j, 1, n}, {k, 1, n}], Reals];
Subscript["F", μσ] -> MatrixForm[F]
f=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] F[[k, l]],
{k, 1, n}, {l, 1, n}], {i, 1, n}, {j, 1, n}], Reals];
"F"^μσ -> MatrixForm[f]
                                                                        "Christoffelsymbole"
chr=Simplify[Table[(1/2)Sum[(it[[i, s]])
(D[mt[[s, j]], x[[k]]]+D[mt[[s, k]], x[[j]]] -D[mt[[j, k]], x[[s]]]), {s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}]];
crs=Table[If[UnsameQ[chr[[i, j, k]], 0],
{ToString[Γ[i, j, k]], chr[[i, j, k]]}], {i, 1, n}, {j, 1, n}, {k, 1, j}];
TableForm[Partition[DeleteCases[Flatten[crs], Null], 2]]                   
                                                                            "Riemann Tensor"
rmn=Simplify[Table[
D[chr[[i, j, l]], x[[k]]] - D[chr[[i, j, k]], x[[l]]] +
Sum[chr[[s, j, l]] chr[[i, k, s]] -
chr[[s, j, k]] chr[[i, l, s]],
{s, 1, n}], {i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
rie=Table[If[UnsameQ[rmn[[i, j, k, l]], 0],
{ToString[R[i, j, k, l]], rmn[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, k - 1}];
TableForm[Partition[DeleteCases[Flatten[rie], Null], 2]]
                                                                              "Ricci Tensor"
rcc=Simplify[Table[
Sum[rmn[[i, j, i, l]], {i, 1, n}], {j, 1, n}, {l, 1, n}]];
Subscript["Ř", μσ] -> MatrixForm[rcc]
ric=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] rcc[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"Ř"^μσ -> MatrixForm[ric]
                                                                              "Ricci Skalar"
Ř=Simplify[Sum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ř"->Ř
                                                            (* kovarianter Riemann Tensor *)
rcv=Table[Sum[mt[[i, j]] rmn[[j, k, l, m]], {j, 1, 4}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
                                                        (* kontravarianter Riemann Tensor *)
rcn=Table[Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] rcv[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, 4}, {h, 1, n}, {o, 1, n}, {p, 1, n}];
                                                                        "Kretschmann Skalar"
krn= Sum[rcv[[i, j, k, l]] rcn[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
"K"->FullSimplify[krn]
                                                                           "Einstein Tensor"
est=Simplify[rcc-Ř mt/2];
Subscript["G", μσ] -> MatrixForm[est]
ein=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] est[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"G"^μσ -> MatrixForm[Simplify[ein]]

rplc[y_]:=(((((((y/.t->t[τ])/.r->r[τ])/.θ->θ[τ])/.φ->φ[τ])/.Derivative[1][t[τ]]->
t'[τ])/.Derivative[1][r[τ]]->r'[τ])/.Derivative[1][θ[τ]]->θ'[τ])/.Derivative[1][φ[τ]]->φ'[τ];
list[y_]:=y[[1]]==y[[2]];
                                                                      "Bewegungsgleichungen"
geo=Simplify[Table[-Sum[
chr[[i, j, k]] x[[j]]' x[[k]]'+q f[[i, k]] x[[j]]' mt[[j, k]],
{j, 1, n}, {k, 1, n}], {i, 1, n}]];

equ=Table[{x[[i]]''[τ]==Simplify[rplc[geo[[i]]], Reals]}, {i, 1, n}];

geodesic1=equ[[1]][[1]]
geodesic2=equ[[2]][[1]]
geodesic3=equ[[3]][[1]]
geodesic4=equ[[4]][[1]]
                                                                     "totale Zeitdilatation"
H=Sum[mt[[μ, ν]] x[[μ]]' x[[ν]]', {μ, 1, n}, {ν, 1, n}];                        
ṫ=Table[Quiet[rplc[Simplify[Normal[Solve[
-μ==(H/.t'->ť), ť]]][[j, 1, 2]]]], {j, 1, 2}];                        
Derivative[1][t][τ]->ṫ[[1]] || ṫ[[2]]
                                                                  "kovarianter Viererimpuls"
p[μ_]:=-(Sum[mt[[μ, ν]]*x[[ν]]', {ν, 1, n}]+q A[[μ]]);
pt[τ]->rplc[Simplify[p[1], Reals]]
pr[τ]->rplc[Simplify[p[2], Reals]]
pθ[τ]->rplc[Simplify[p[3], Reals]]
pφ[τ]->rplc[Simplify[p[4], Reals]]
                                                                    "lokale Geschwindigkeit"
V[x_]:=Simplify[Normal[Solve[vx Sqrt[-mt[[x, x]]]/Sqrt[1-μ^2 v[τ]^2]-(1-μ^2 v^2) q A[[x]]==
p[x], vx]][[1, 1]], Reals];                                                   
rplc[V[2]]/.vx->vr[τ]
rplc[V[3]]/.vx->vθ[τ]
rplc[V[4]]/.vx->vφ[τ]












#7 Geodätische Gleichung, Kerr-Schild:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* | Mathematica Syntax | GEODESIC SOLVER | geodesics.yukterez.net | Version 23.12.2019 | *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

ClearAll["Global`*"]
                                               (* Input: kovariante metrische Komponenten *)
g11=gtt=1-ц;
g12=gtr=-ц;
g13=gtθ=0;
g14=gtφ=ц a Sin[θ]^2;
g22=grr=-1-ц;
g23=grθ=0;
g24=grφ=a(1+ц)Sin[θ]^2;
g33=gθθ=-Σ;
g34=gθφ=0;
g44=gφφ=-χ/Σ Sin[θ]^2;
                                                                           (* Abkürzungen *)
Σ=r^2+a^2 Cos[θ]^2;
Δ=r^2-2 r+a^2;
χ=(r^2+a^2)^2-a^2 Sin[θ]^2 Δ;
ц=2r/Σ;
              (* Koordinaten, Dimensionen, magnetisches Monopol, elektrische Ladung, Spin *)
x={t, r, θ, φ}; n=4; P=0; Ω=℧; ℧=℧; a=a;
                                                                         "Metrischer Tensor"
mt={{g11, g12, g13, g14}, {g12, g22, g23, g24}, {g13, g23, g33, g34}, {g14, g24, g34, g44}};
Subscript["g", μσ] -> MatrixForm[mt]
it=Simplify[Inverse[mt]];
"g"^μσ -> MatrixForm[it]
                                                                            "Maxwell Tensor"
A={0, 0, 0, 0};
F=Simplify[Table[((D[A[[j]], x[[k]]]-D[A[[k]], x[[j]]])), {j, 1, n}, {k, 1, n}], Reals];
Subscript["F", μσ] -> MatrixForm[F]
f=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] F[[k, l]],
{k, 1, n}, {l, 1, n}], {i, 1, n}, {j, 1, n}], Reals];
"F"^μσ -> MatrixForm[f]
                                                                        "Christoffelsymbole"
chr=Simplify[Table[(1/2)Sum[(it[[i, s]])
(D[mt[[s, j]], x[[k]]]+D[mt[[s, k]], x[[j]]] -D[mt[[j, k]], x[[s]]]), {s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}]];
crs=Table[If[UnsameQ[chr[[i, j, k]], 0],
{ToString[Γ[i, j, k]], chr[[i, j, k]]}], {i, 1, n}, {j, 1, n}, {k, 1, j}];
TableForm[Partition[DeleteCases[Flatten[crs], Null], 2]]                   
                                                                            "Riemann Tensor"
rmn=Simplify[Table[
D[chr[[i, j, l]], x[[k]]] - D[chr[[i, j, k]], x[[l]]] +
Sum[chr[[s, j, l]] chr[[i, k, s]] -
chr[[s, j, k]] chr[[i, l, s]],
{s, 1, n}], {i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
rie=Table[If[UnsameQ[rmn[[i, j, k, l]], 0],
{ToString[R[i, j, k, l]], rmn[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, k - 1}];
TableForm[Partition[DeleteCases[Flatten[rie], Null], 2]]
                                                                              "Ricci Tensor"
rcc=Simplify[Table[
Sum[rmn[[i, j, i, l]], {i, 1, n}], {j, 1, n}, {l, 1, n}]];
Subscript["Ř", μσ] -> MatrixForm[rcc]
ric=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] rcc[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"Ř"^μσ -> MatrixForm[ric]
                                                                              "Ricci Skalar"
Ř=Simplify[Sum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ř"->Ř
                                                            (* kovarianter Riemann Tensor *)
rcv=Table[Sum[mt[[i, j]] rmn[[j, k, l, m]], {j, 1, 4}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
                                                        (* kontravarianter Riemann Tensor *)
rcn=Table[Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] rcv[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, 4}, {h, 1, n}, {o, 1, n}, {p, 1, n}];
                                                                        "Kretschmann Skalar"
krn= Sum[rcv[[i, j, k, l]] rcn[[i, j, k, l]],
{i, 1, 4}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
"K"->FullSimplify[krn]
                                                                           "Einstein Tensor"
est=Simplify[rcc-Ř mt/2];
Subscript["G", μσ] -> MatrixForm[est]
ein=Simplify[Table[Sum[
it[[i, k]] it[[j, l]] est[[k, l]], {k, 1, n}, {l, 1, n}],
{i, 1, n}, {j, 1, n}], Reals];
"G"^μσ -> MatrixForm[Simplify[ein]]

rplc[y_]:=(((((((y/.t->t[τ])/.r->r[τ])/.θ->θ[τ])/.φ->φ[τ])/.Derivative[1][t[τ]]->
t'[τ])/.Derivative[1][r[τ]]->r'[τ])/.Derivative[1][θ[τ]]->θ'[τ])/.Derivative[1][φ[τ]]->φ'[τ];
list[y_]:=y[[1]]==y[[2]];
                                                                      "Bewegungsgleichungen"
geo=Simplify[Table[-Sum[
chr[[i, j, k]] x[[j]]' x[[k]]'+q f[[i, k]] x[[j]]' mt[[j, k]],
{j, 1, n}, {k, 1, n}], {i, 1, n}]];

equ=Table[{x[[i]]''[τ]==Simplify[rplc[geo[[i]]], Reals]}, {i, 1, n}];

geodesic1=equ[[1]][[1]]
geodesic2=equ[[2]][[1]]
geodesic3=equ[[3]][[1]]
geodesic4=equ[[4]][[1]]
                                                                     "totale Zeitdilatation"
H=Sum[mt[[μ, ν]] x[[μ]]' x[[ν]]', {μ, 1, n}, {ν, 1, n}];                        
ṫ=Table[Quiet[rplc[Simplify[Normal[Solve[
-μ==(H/.t'->ť), ť]]][[j, 1, 2]]]], {j, 1, 2}];                        
Derivative[1][t][τ]->ṫ[[1]] || ṫ[[2]]
                                                                  "kovarianter Viererimpuls"
p[μ_]:=-(Sum[mt[[μ, ν]]*x[[ν]]', {ν, 1, n}]+q A[[μ]]);
pt[τ]->rplc[Simplify[p[1], Reals]]
pr[τ]->rplc[Simplify[p[2], Reals]]
pθ[τ]->rplc[Simplify[p[3], Reals]]
pφ[τ]->rplc[Simplify[p[4], Reals]]
                                                                    "lokale Geschwindigkeit"
V[x_]:=Simplify[Normal[Solve[vx Sqrt[-mt[[x, x]]]/Sqrt[1-μ^2 v[τ]^2]-(1-μ^2 v^2) q A[[x]]==
p[x], vx]][[1, 1]], Reals];                                                   
rplc[V[2]]/.vx->vr[τ]
rplc[V[3]]/.vx->vθ[τ]
rplc[V[4]]/.vx->vφ[τ]














#8 Schatten, 2D:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || Mathematica Syntax | BLACK HOLE SHADOWS | kerr.yukterez.net | Version 03.10.2017 || *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

rE=M+Sqrt[M^2-a^2 Cos[θ]^2]; re={Sqrt[rE^2+a^2] Sin[θ],rE Cos[θ]};
rG=M-Sqrt[M^2-a^2 Cos[θ]^2]; rg={Sqrt[rG^2+a^2] Sin[θ],rG Cos[θ]};
rA=M+Sqrt[M^2-a^2]; ra={Sqrt[rA^2+a^2] Sin[θ],rA Cos[θ]};
rI=M-Sqrt[M^2-a^2]; ri={Sqrt[rI^2+a^2] Sin[θ],rI Cos[θ]};
A=Interpolation[{{0,0},{0.1,0.21},{0.2,0.4},{0.3,0.61},{0.4,0.82},{0.5,1.01},{0.6,1.24},{0.7,1.48},
{0.8,1.71},{0.866,1.9},{0.9,2.01},{0.95,2.17},{0.98,2.3},{0.99,2.38},{0.999,2.47},{1,2.5}},
InterpolationOrder -> 1];
B=Interpolation[{{0,Sqrt[27]},{0.1,5.19},{0.2,5.18},{0.3,5.16},{0.4,5.14},{0.5,5.11},{0.6,5.07},
{0.7,5.02},{0.8,4.93},{0.866,4.86},{0.9,4.82},{0.95,4.74},{0.98,4.68},{0.99,4.65},{0.999,4.62},{1,4.6}},
InterpolationOrder -> 1];
pp:=ParametricPlot[{re,rg,ra,ri},{θ,0,2π},
Frame->True,ImageSize->400,PlotRange->{{-8,8},{-6,6}},PlotStyle->{{Black,Thick}}];
cp:=ContourPlot[(x^2+y^2+A[a] x)^2-B[a]^2 (x^2+y^2)==0,{X,-8,8},{y,-6,6},ContourStyle->{Red,Thick}];
a=Sin[w]; M=1; x=-X; Do[Print[Rasterize[Grid[{{Show[pp,cp]},{" a"->N[a]}},
Alignment->Left]]],
{w,0,π/2,π/200}]















#9 Schatten, 3D:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || Mathematica Syntax | BLACK HOLE SHADOWS | kerr.yukterez.net | Version 03.10.2017 || *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

Manipulate[

rE=1+Sqrt[1-a^2 Cos[θ]^2]; re={Sqrt[rE^2+a^2] Sin[θ] Cos[φ], Sqrt[rE^2+a^2] Sin[θ] Sin[φ], rE Cos[θ]};
rG=1-Sqrt[1-a^2 Cos[θ]^2]; rg={Sqrt[rG^2+a^2] Sin[θ] Cos[φ], Sqrt[rG^2+a^2] Sin[θ] Sin[φ], rG Cos[θ]};
rA=1+Sqrt[1-a^2]; ra={Sqrt[rA^2+a^2] Sin[θ] Cos[φ], Sqrt[rA^2+a^2] Sin[θ] Sin[φ], rA Cos[θ]};
rI=1-Sqrt[1-a^2]; ri={Sqrt[rI^2+a^2] Sin[θ] Cos[φ], Sqrt[rI^2+a^2] Sin[θ] Sin[φ], rI Cos[θ]};

rot[{x_, y_, z_}, w_]:={x, y Sin[w]-z Cos[w], y Cos[w]+z Sin[w]};

pp:=Show[
ParametricPlot3D[rot[re, ϑ], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> 20, PlotStyle -> Directive[Gray, Opacity[0.10]],
ImageSize->400, PlotRange->{{-8, 8}, {-8, 8}, {-6, 6}},
ViewPoint->{0, 20, 0}, ImagePadding->1],
ParametricPlot3D[rot[ra, ϑ], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> 20, PlotStyle -> Directive[Gray, Opacity[0.15]]],
ParametricPlot3D[rot[ri, ϑ], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> 20, PlotStyle -> Directive[Gray, Opacity[0.25]]],
ParametricPlot3D[rot[rg, ϑ], {φ, 0, 2 π}, {θ, 0, π},
Mesh -> None, PlotPoints -> 20, PlotStyle -> Directive[Gray, Opacity[0.35]]]];
                       
α=Interpolation[{{0,0},{0.1,0.21},{0.2,0.4},{0.3,0.61},{0.4,0.82},{0.5,1.01},{0.6,1.24},{0.7,1.48},
{0.8,1.71},{0.866,1.9},{0.9,2.01},{0.95,2.17},{0.98,2.3},{0.99,2.38},{0.999,2.47},{1,2.5}},
InterpolationOrder -> 1];

β=Interpolation[{{0,Sqrt[27]},{0.1,5.19},{0.2,5.18},{0.3,5.16},{0.4,5.14},{0.5,5.11},{0.6,5.07},
{0.7,5.02},{0.8,4.93},{0.866,4.86},{0.9,4.82},{0.95,4.74},{0.98,4.68},{0.99,4.65},{0.999,4.62},{1,4.6}},
InterpolationOrder -> 1];

A[a_]:=α[a] Sin[ϑ]+a Sin[ϑ]^3 Cos[ϑ]^2/5;
B[a_]:=β[a]+0.23 Cos[ϑ]^4(1-Sqrt[1-a^4]);

cp:=ContourPlot3D[(x^2+y^2+A[a] x)^2-B[a]^2 (x^2+y^2)==0, {x, -8, 8}, {z, -3, 3}, {y, -6, 6}, ContourStyle->{Black, Thick}, PlotPoints -> 20];

Rasterize[Grid[{{Show[pp, cp]}, {" a"->N[a]}},
Alignment->Left]],
{{ϑ, π/2}, 0, π/2}, {{a, 1}, 0, 1}]















[Yukterez]

Tatsächlich veschwindender axialer Drehimpuls Lz:
Animationsparameter: Koordinatenzeit t, a=1, r0=1+√2, v0=vz0=vθ0=1, vφ0=vr0=0, θ0=π/2:

  ←

Scheinbar veschwindender, aber negativer axialer Drehimpuls Lz:
Animationsparameter: Koordinatenzeit t, a=1, r0=3, v0=1, vφ0=-1/3, vθ0=√8/3, vr0=0, θ0=π/2:

  ←

Photonenorbit innerhalb der Ergosphäre:
Animationsparameter: Koordinatenzeit t, a=1, r0=1.448, v0=1, vφ0=0.404518, vθ0=0.91453, vr0=0, θ0=π/2:

  ←

Animationsparameter: Spin a, r=3, t=300 (beobachteter Inklinationswinkel: 90°)

  ←

[Yukterez]

Animationsparameter: Koordinatenzeit t, a=0.646, x0=7, y0=z0=0, i0=π/2-arctan(5/6), v0=0.4

  ←

Selbe Bedingungen bei Spinparameter a=0.628

  ←

Selbe Bedingungen bei Spinparameter a=0.623

  ←

Prograder gebundener Orbit .
a=0.9, v0=0.4, θ0=π/2, r0=7, i0=arctan(5/6)

  ←

Mit reflektiertem Inklinationswinkel i0 .
a=0.9, v0=0.4, θ0=π/2, r0=7, i0=π/2-arctan(5/6)

  ←

Freier Fall aus der lokalen Ruhelage .
Animationsparameter: Koordinatenzeit t, r0=4GM/c², θ0=π/4, v0=0

  ←

Plunge Orbit mit neutonischer Orbital- und Fluchtgeschwindigkeit.
v0=vθ0=vz0=√(1GM/r0) → Q=4.5, E=0.749859 (1. Teil)
v0=vθ0=vz0=√(2GM/r0) → Q=18.0, E=1.06046 (2. Teil)
a=0.998, r0=3GM/c², θ0=π/2, Lz=0 (beide Teile)

  ←

Selbe Situation in horizontüberschreitenden Kerr-Schild Koordinaten: hier entlang  ←

Zackiger Orbit (retrograd) .
Animationsparameter: Koordinatenzeit t, a=0.95, v0=-0.5, vφ0=-sin(11/50)/2=-0.109115, vθ0=-cos(11/50)/2=-0.487949, E=0.956545, Lz=-0.830327, Q=13.4126, pθ0=-3.66233, pr0=0, r0=6.5, θ0=π/2, i0=π/2-11/50=77.3949°

  ←

Die gestrichelte Linie zeigt die Bahn eines ZAMO auf fixem r0.

Abschuss auf der polaren Achse ohne axialen Drehimpuls (Lz=0) .
Startbedingungen: R0=5, θ0=π/2, v0=vz0=vθ0=51/50·√((1/5)/(1-2/5))
Animationsparameter: Koordinatenzeit t

a=0 (Schwarzschild Limit)

  ←

a=0.1

  ←

a=0.998 (Thorne Limit)

  ←

Bahndrehimpulsfreier Wurf mit Fluchtgeschwindigkeit aus dem Inneren der Ergosphäre .
Animationsparameter: Koordinatenzeit t, a=0.998, r0=1.001 rH, v0=vr0=vesc, vφ0=0, vθ0=0, θ0=π/2:

  ←

θ0=π/4:

  ←

θ0=1/1000:

  ←

weitere Startwinkel zum durchklicken.

[Yukterez]

rH: Ereignishorizonte, rE: Ergosphären (in Boyer-Lindquist Koordinaten)



r,θ,φ (links) vs x,y,z (rechts):



Farbcode: hellblau = äußere Ergosphäre, cyan = äußerer Horizont, violett = innerer Horizont, Rot = innere Ergosphäre



Alle relevanten Flächen; die Ringsingularität befindet sich auf der Äquatorebene der inneren Ergosphäre:



Der Spinparameter in der oberen Illustration beträgt a=0.99Jc/G/M². In den oberen Plots ist die gravitative Masse M gleich 1 gesetzt; für eine Animation mit Mirr=1 klick hier.

Code:

Code: Alles auswählen

(* Perspektive *)
rE = 1 + Sqrt[1 - a^2 Cos[θ]^2]; RE[A_] := {Sqrt[rE^2 + A^2] Sin[θ] Cos[φ], Sqrt[rE^2 + A^2] Sin[θ] Sin[φ], rE Cos[θ]};
rA = 1 + Sqrt[1 - a^2]; RA[A_] := {Sqrt[rA^2 + A^2] Sin[θ] Cos[φ], Sqrt[rA^2 + A^2] Sin[θ] Sin[φ], rA Cos[θ]};
rI = 1 - Sqrt[1 - a^2]; RI[A_] := {Sqrt[rI^2 + A^2] Sin[θ] Cos[φ], Sqrt[rI^2 + A^2] Sin[θ] Sin[φ], rI Cos[θ]};
rG = 1 - Sqrt[1 - a^2 Cos[θ]^2]; RG[A_] := {Sqrt[rG^2 + A^2] Sin[θ] Cos[φ], Sqrt[rG^2 + A^2] Sin[θ] Sin[φ], rG Cos[θ]};
horizons[A_] := Show[
Graphics3D[{}, SphericalRegion -> True, ViewPoint -> {0, -10 Cos[w] + 10 Sin[w], 10 Cos[w] + 10 Sin[w]}, ImageSize -> 340, PlotRange -> 3],
ParametricPlot3D[RE[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Blue, Opacity[0.1]]],
ParametricPlot3D[RA[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Cyan, Opacity[0.15]]],
ParametricPlot3D[RI[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Red, Opacity[0.2]]],
ParametricPlot3D[RG[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Red, Opacity[0.5]]]];
a = 0.99;
Do[Print[Rasterize[Grid[{{horizons[a], horizons[0]}}]]], {w, 0, 2 π, π/125}]

Code: Alles auswählen

(* Spinparameter *)
rE = 1 + Sqrt[1 - a^2 Cos[θ]^2]; RE[A_] := {Sqrt[rE^2 + A^2] Sin[θ] Cos[φ], Sqrt[rE^2 + A^2] Sin[θ] Sin[φ], rE Cos[θ]};
rA = 1 + Sqrt[1 - a^2]; RA[A_] := {Sqrt[rA^2 + A^2] Sin[θ] Cos[φ], Sqrt[rA^2 + A^2] Sin[θ] Sin[φ], rA Cos[θ]};
rI = 1 - Sqrt[1 - a^2]; RI[A_] := {Sqrt[rI^2 + A^2] Sin[θ] Cos[φ], Sqrt[rI^2 + A^2] Sin[θ] Sin[φ], rI Cos[θ]};
rG = 1 - Sqrt[1 - a^2 Cos[θ]^2]; RG[A_] := {Sqrt[rG^2 + A^2] Sin[θ] Cos[φ], Sqrt[rG^2 + A^2] Sin[θ] Sin[φ], rG Cos[θ]};
horizons[A_] := Show[
Graphics3D[{}, SphericalRegion -> True, ViewPoint -> {0, 10, 5}, ImageSize -> 340, PlotRange -> 3],
ParametricPlot3D[RE[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Blue, Opacity[0.1]]],
ParametricPlot3D[RA[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Cyan, Opacity[0.15]]],
ParametricPlot3D[RI[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Red, Opacity[0.2]]],
ParametricPlot3D[RG[A], {φ, 0, 2 π}, {θ, 0, π}, Mesh -> None, PlotStyle -> Directive[Red, Opacity[0.5]]]];
Do[Print[Rasterize[Grid[{{horizons[a], horizons[0]}}]]], {a, 0, 1, 1/250}]

[Yukterez]

Die Bedingung für die radiale Beschleunigung und den radialen Impuls auf einer Kreisbahn ist



Um die lokale Kreisbahngeschwindigkeit (relativ zum ZAMO) für einen Orbit auf gegebenem r mit gegebenem a zu erhalten wird mit v=vφ, vθ=0, θ=π/2 nach vφ aufgelöst. Diese Gleichung hat 2 Lösungen, wovon die kleinere prograd und die größere retrograd ist:



Der pro- und retrograde Photonenradius liegt damit bei



und wenn vφ=0, v=vθ gesetzt wird der poloidiale mit Lz=0 (einem lokalen Inklinationswinkel von 90°, siehe Orbit 1) bei



Wegen der Korotation lokaler Inertialsysteme fährt das Photon dann trotz dem es keinen axialen Drehimpuls besitzt mit der örtlichen Frame-Dragging-Rate die Ф-Achse entlang:

  ←

Für ein Photon mit genau so viel (negativem) axialem Drehimpuls um das Frame-Dragging am Äquator zu kompensieren ergibt sich für alle Spinparameter die Boyer-Lindquist-Radialkoordinate

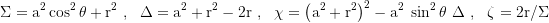
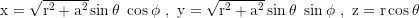
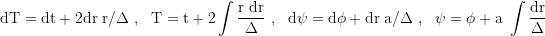
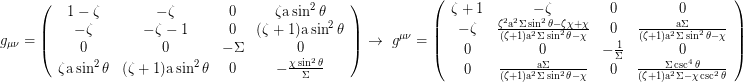
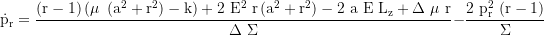
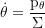
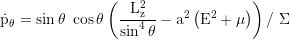
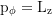
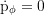
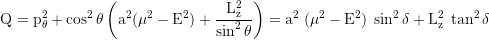
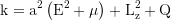
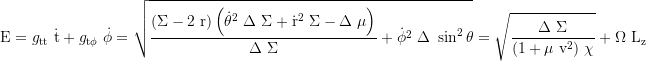
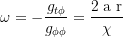
, also der klassische Schwarzschild-Photonenkreisbahnradius (siehe Orbit 2)

Die zu kompensierende Frame-Dragging-Geschwindigkeit beträgt bei maximalem Spin c/3, weshalb der äquatoriale Inklinationswinkel δ0=π/2+ArcSin(1/3) ist, damit die lokale Geschwindigkeitskomponente des Photons gegen die Ф-Achse vФ nach Pythagoras genau c/3 ist:

  ←

Auf r=3 ergibt sich für alle a ein beobachteter äquatorialer Inklinationswinkel von 90°: Vergleich

Um den von a und r abhängigen Inklinationswinkel für einen Photonenorbit mit Startposition auf der Äquatorebene zu finden wird v0=1, μ=0, vr0=0, pr'0=0 gesetzt und nach δ0 aufgelöst. Dann ergibt sich:



mit









Alle geschlossenen Photonenbahnen haben einen konstanten Boyer-Lindquist-Radius, weswegen die Form der abgefahrenen Sphären in kartesischen Koordinaten ein Ellipsoid ergibt.

Animation aller Photonenorbits für den Spinparameter a=1Jc/G/M² (für eine erweiterte Ansicht das Bild anklicken):

  ←

Herleitung: hier entlang, weiterführender Beitrag: klick

Pro- und retrograde Kreisbahngeschwindigkeit als Funktion von a und r:



Schwarzschildlimit:



Astrophysikalisches Limit:



Extreme Kerr:



x-Achse: Boyer-Lindquist r, y-Achse: v lokal

Code:

Code: Alles auswählen

ClearAll["Global`*"]

vretro[a_,r_]:=(a^2+2 a Sqrt[r]+r^2)/(Sqrt[a^2+(-2+r) r] (a-r^(3/2)));
vpro[a_,r_]:=(a^2-2 a Sqrt[r]+r^2)/(Sqrt[a^2+(-2+r) r] (a+r^(3/2)));

rh = 1 + Sqrt[1 - a^2];
r1 = 2 (1 + Cos[2/3 ArcCos[-a]]);
r2 = 2 (1 + Cos[2/3 ArcCos[+a]]);

Do[Print[Rasterize[Grid[{{
Plot[{vpro[a, r], vretro[a, r]}, {r, 1, 10},
PlotRange->{{1, 10}, {-1, 1}},
GridLines->{{rh, r1, r2}, {}},
Frame->True, ImageSize->400]},
{"a"->a}}, Alignment->Left]]],
{a, 0, 1, 0.2}]

[Yukterez]

Die mitrotierenden Punkte zeigen lokal ruhende Inertialsysteme LNRFs (locally nonrotating frames) auf denen ZAMOs (zero angular momentum observers) auf konstantem r,θ mit der Frame-Dragging-Rate mitbewegt werden. Darstellung im Inertialsystem eines ZAVOs (zero angular velocity oberservers) at infinity (mit a=1Jc/G/M²):



ZAMO (magenta), FIDO (cyan) & FREFO (rot) im Bezugssystem des ZAVO:

  ←

Benötigte Formeln:

Framedragging Winkelgeschwindigkeit



Axialer Gyrationsradius



Kartesischer Umfangsradius



Gravitative Zeitdilatation



Die im System des Buchhalters (ZAVO) beobachtete Transversalgeschwindigkeit der lokal stationären Boje (ZAMO) ist



während die lokal stationäre Boje (ZAMO) misst dass eine zum Buchhalter stationäre und damit relativ zum Strudel bewegte Boje (FIDO) mit



an ihr vorbeifliegt.

weiterführender Beitrag: hier entlang

[Yukterez]

Bestimmung der radialen physikalischen Distanz:

Das voll ausgeschriebene Linienelement der Kerr-Metrik in BL-Koordinaten ist

                            

Das wird mit a=0 zur Schwarzschild-Metrik in Schwarzschild-Koordinaten

                            

Für die radiale Strecke wird die Wurzel des roten Terms (g_rr) von r1 bis r2 integriert, für die poloidiale Strecke die des grünen Terms (g_θθ) von θ1 bis θ2, und für die axiale Strecke die des blauen Terms (g_ФФ) von Ф1 bis Ф2. Wenn die Strecke nicht nur auf einer Achse sondern auf mehreren verläuft oder man den Platz auf einer Fläche bzw. den Inhalt eines Volumens betrachtet muss die gekoppelte Differentialgleichung über alle betroffenen Koordinaten integriert werden.

Beispiel: die radiale Strecke vom Schwarzschildradius r1=rs=2GM/c² bis r2=2.1GM/c², also Δr=0.1, ergibt mit a=0 die physikalische Strecke ΔR=0.901826GM/c²:

und mit a=Jc/G/M²=1 je nach Polwinkel knapp über oder unter ΔR≈0.2GM/c²:

Einbettungsdiagramm:



Wenn man von einer r-Koordinate zur anderen rechnet gilt: je stärker die Rotation, desto geringer die radiale Längenkontraktion, aber desto größer dafür die axiale. Das kommt daher dass der Horizont sich bei steigender Rotation nach hinten verschiebt.

Rechnen wir nicht vom Schwarzschildradius r1=rs=2 weg, sondern vom Ereignishorizont r1=rH=1+√(1-a²), dann werden die Δr=0.1 mit steigendem a zu einem sehr viel höherem ΔR. Bei a=1 würde die radiale Strecke bis zum Ereignishorizont sogar unendlich, siehe Bardeen 1972:



was wegen dem a≤0.998-Limit und der komischen Zensur in der Natur aber nicht vorkommt. Plot von a=0 bis a=1:

Einbettungsdiagramm:



Mit dem praktischen Maximum von a=0.998 beträgt die Strecke bis zum Ereignishorizont in diesem Beispiel

Selbes Einbettungsdiagramm mit Fokus auf a=0.998:



ΔR für r1=rH und r2=r1+0.1 (also Δ=0.1) bei a=0.998 und θ=π/2:



Originalbeitrag: hier entlang

Nächstes Kapitel:

[Yukterez]

verwandte Themen: Kerr Newman || Reissner Nordström || Schwarzschild || Gravitationslinsen || Raytracing || Paraboloid


Letzte unvandalierte Version auf Wikipedia: 170808900

Referenzen, weiterführende Literatur und empfohlene Links:
The Kerr Metric || The Kerr-Newman Metric || Kerr Newman Motion || Periodic Table for Black Hole Orbits || Exact Solution for the Kerr Separatrix 1, 2 || The Spinning Black Hole || Madore || Black Hole Penrose Diagrams || Infinite Redshift Surfaces || Universe in Problems || Tapir 26 || Tapir 27 || Odyssey Edu || Horizon Skimming Orbits || Black Holes Introduction || Rigidly rotating ZAMO surfaces || Global Structure of the Kerr Family || Fuerst & Wu || Bolin & Bengtsson: The Angular Momentum of Kerr Black Holes || Roy Kerr 1963 (Original Work) || Raine || James Bardeen 1972 || Shahar Hod 2012 || Hughes 2000 || Claudel et al || Ed Teo || Nülifer et al || Hanauske || Interstellar || Gyoto || Catalogue of Spacetimes || Stellar Charge || Ynogkm || CERN Geodesics Shortcut || Van der Wijk || The interplay between forces in the Kerr–Newman field || Komissarov: Kerr Schild, Electrodynamics || Binary Kerr Merger || De Mees: Rotating Torus || Chrusciel || Tendex & Vortex || Faraoni || Kerr Dual Merger || Multipole Neutron Stars || Multipole Rotating Stars || Shadows || Plasma Shadows || Ring Singularity || BL vs KS Hydrodynamics || Photon motion in Kerr-DeSitter || G-Ray Shadows || Geokerr || Kerr 599 || Kuchelmeister || Null Geodesics || Axialsymmetric Shadows || Nut Lambda Black Holes || GeoVis || Strong Lensing || Hairy BH Notebooks || Interior mass formula || Sebastien Garmier: cuRRay || NumRel 99 || Horizon Mass Theorem || Newman Janis Derivation || Photon orbits around naked singularities

Animations by Simon Tyran, Vienna (Yukterez) - reuse permitted under the Creative Commons License CC BY-SA 4.0