
 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  The english version is available on en.yukterez.net
The english version is available on en.yukterez.net
Verwandte Beiträge: KNdS || Kerr Newman || Kerr || Schwarzschild || De Sitter || Gravitationslinsen || Raytracing || Flammsches Paraboloid

● Feldgleichungs- und Geodätensolver:

 Der obere Solver ist mit der KNdS-Metrik in {t,r,θ,φ}-BL-Koordinaten voreingestellt. Mit Λ=0 reduziert sich die Metrik auf Kerr Newman, mit Λ=℧=0 auf Kerr, mit Λ=a=0 auf Reissner Nordström, mit Λ=℧=a=0 auf Schwarzschild, mit ℧=a=0 auf Schwarzschild De Sitter, mit ℧=a=M=0 auf De Sitter und mit Λ=℧=a=M=0 auf Minkowski. Der untere Solver ist auf die Kerr Newman Metrik in kartesischen Kerr Schild Koordinaten eingestellt (da die Metrik in diesen Koordinaten sehr kompliziert wird benötigt dieser sehr viel mehr Rechenzeit). Falls das Linienelement in einer unübersichtlichen Form vorliegt können die metrischen Koeffizienten mit dem Linienelementzerleger sauber getrennt und hernach in den Solver eingegeben werden.
Der obere Solver ist mit der KNdS-Metrik in {t,r,θ,φ}-BL-Koordinaten voreingestellt. Mit Λ=0 reduziert sich die Metrik auf Kerr Newman, mit Λ=℧=0 auf Kerr, mit Λ=a=0 auf Reissner Nordström, mit Λ=℧=a=0 auf Schwarzschild, mit ℧=a=0 auf Schwarzschild De Sitter, mit ℧=a=M=0 auf De Sitter und mit Λ=℧=a=M=0 auf Minkowski. Der untere Solver ist auf die Kerr Newman Metrik in kartesischen Kerr Schild Koordinaten eingestellt (da die Metrik in diesen Koordinaten sehr kompliziert wird benötigt dieser sehr viel mehr Rechenzeit). Falls das Linienelement in einer unübersichtlichen Form vorliegt können die metrischen Koeffizienten mit dem Linienelementzerleger sauber getrennt und hernach in den Solver eingegeben werden.
● Beispiele verschiedener Metriken in unterschiedlichen Koordinaten:

 Boyer Lindquist ist das rotierende Äquivalent zu Droste (Koordinatenzeit eines stationären feldfreien Beobachters), Kerr-Schild zu Finkelstein (Koordinatenzeit wird per einfallenden Lichtstrahlen aufgestempelt) und Doran zu Raindrop Koordinaten (t wird durch mit der negativen Fluchtgeschwindigkeit freifallende Uhren definiert). In den Bewegungsgleichungen sind die Koordinaten Funktionen der Eigenzeit bzw. bei Photonen des affinen Parameters (t→t[τ], r'→r'[τ], θ''→θ''[τ] usw), in manchen Beispielen mit kilometerlangem Output wird dies der Kürze wegen und da es sich sowieso aus dem Zusammenhang ergibt nicht extra angeschrieben (die rplc Funktion ist dann deaktiviert, im Code ist sie jedoch standardmäßig aktiviert damit der Output bei Bedarf gleich direkt in den Simulator übertragen werden kann). Sofern nicht anders angegeben werden natürliche Einheiten mit G=M=c=K=1 verwendet (Längen haben die Einheit GM/c², Zeiten GM/c³, Geschwindigkeiten c, etc). Der einheitsbehaftete Wert der kosmologischen Konstante ist in unserem Universum Λ=1.1056e-52/m² (im Kontext eines schwarzen Lochs mit M=1e40kg wäre das dimensionslos Λ→G²M²Λ/c⁴=6.0963e-87), wobei die Vakuumdichte ρΛ=c²Λ/(8πG) beträgt.
Boyer Lindquist ist das rotierende Äquivalent zu Droste (Koordinatenzeit eines stationären feldfreien Beobachters), Kerr-Schild zu Finkelstein (Koordinatenzeit wird per einfallenden Lichtstrahlen aufgestempelt) und Doran zu Raindrop Koordinaten (t wird durch mit der negativen Fluchtgeschwindigkeit freifallende Uhren definiert). In den Bewegungsgleichungen sind die Koordinaten Funktionen der Eigenzeit bzw. bei Photonen des affinen Parameters (t→t[τ], r'→r'[τ], θ''→θ''[τ] usw), in manchen Beispielen mit kilometerlangem Output wird dies der Kürze wegen und da es sich sowieso aus dem Zusammenhang ergibt nicht extra angeschrieben (die rplc Funktion ist dann deaktiviert, im Code ist sie jedoch standardmäßig aktiviert damit der Output bei Bedarf gleich direkt in den Simulator übertragen werden kann). Sofern nicht anders angegeben werden natürliche Einheiten mit G=M=c=K=1 verwendet (Längen haben die Einheit GM/c², Zeiten GM/c³, Geschwindigkeiten c, etc). Der einheitsbehaftete Wert der kosmologischen Konstante ist in unserem Universum Λ=1.1056e-52/m² (im Kontext eines schwarzen Lochs mit M=1e40kg wäre das dimensionslos Λ→G²M²Λ/c⁴=6.0963e-87), wobei die Vakuumdichte ρΛ=c²Λ/(8πG) beträgt.
● Koordinatentransformator:

 Transformation von einem Koordinatensystem in ein anderes. Input: vorhandene kovariante Metrik und Transformationsregel für die Koordinaten, Output: neue kovariante Metrik (für die praktische Anwendung siehe das Beispiel unten).
Transformation von einem Koordinatensystem in ein anderes. Input: vorhandene kovariante Metrik und Transformationsregel für die Koordinaten, Output: neue kovariante Metrik (für die praktische Anwendung siehe das Beispiel unten).
● Beispiel zur Koordinatentransformation:

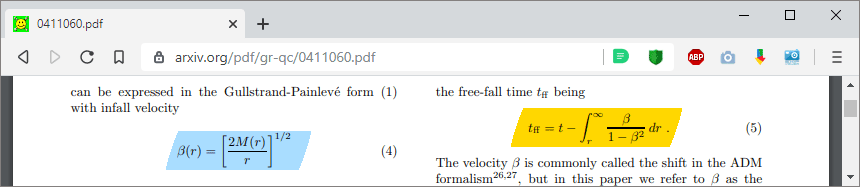
 oben: Transformationsregel, unten: Transformation
oben: Transformationsregel, unten: Transformation
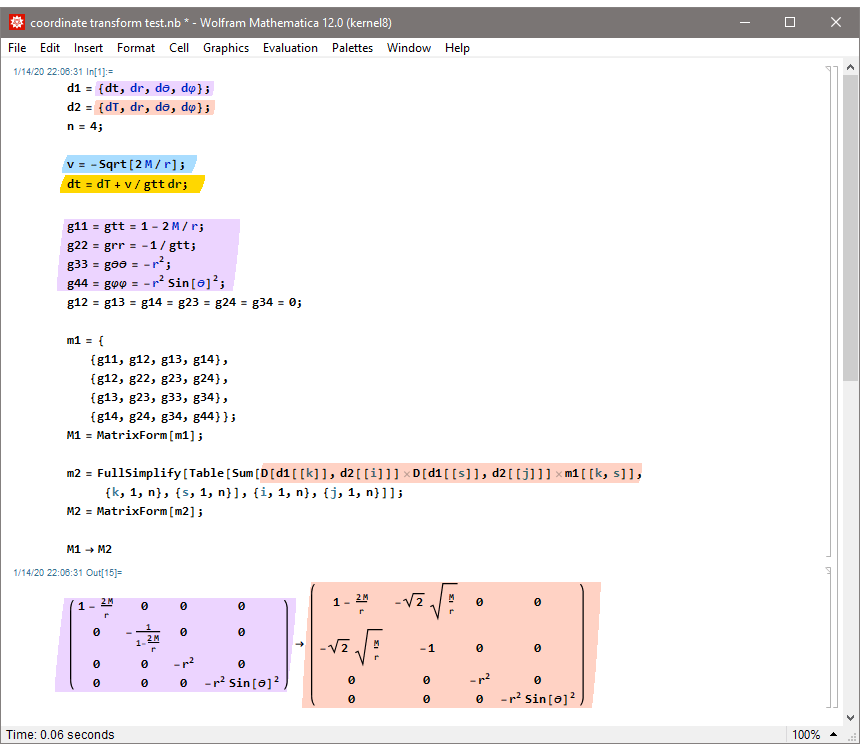
 Beispiel zum Koordinatentransformator: Eingabe der Schwarzschild Metrik in kovarianten Droste Bookkeeper Koordinaten (links) und der Transformationsregel dτ=dt-v·dr/gₜₜ, Ausgabe: Schwarzschild Metrik in kovarianten Gullstrand Painlevé (Raindrop) Koordinaten (rechts). Für die Rücktransformation klick aufs Bild. Äquivalente Transformation für die Kerr Newman Metrik (Boyer Lindquist zu Doran): klick.
Beispiel zum Koordinatentransformator: Eingabe der Schwarzschild Metrik in kovarianten Droste Bookkeeper Koordinaten (links) und der Transformationsregel dτ=dt-v·dr/gₜₜ, Ausgabe: Schwarzschild Metrik in kovarianten Gullstrand Painlevé (Raindrop) Koordinaten (rechts). Für die Rücktransformation klick aufs Bild. Äquivalente Transformation für die Kerr Newman Metrik (Boyer Lindquist zu Doran): klick.
● Funktionsplotter:

 Der Plotter ist auf einen Konturplot des Kretschmann Skalars für die Kerr Newman Metrik eingestellt. Andere Funktionen können aus dem Solver kopiert und eingesetzt werden, wobei bei der Projektion auf die x,z-Ebene die r,θ-Koordinaten als Funktionen von x,z angeschrieben gehören (r→r[x,z,a], θ→θ[x,z,a]).
Der Plotter ist auf einen Konturplot des Kretschmann Skalars für die Kerr Newman Metrik eingestellt. Andere Funktionen können aus dem Solver kopiert und eingesetzt werden, wobei bei der Projektion auf die x,z-Ebene die r,θ-Koordinaten als Funktionen von x,z angeschrieben gehören (r→r[x,z,a], θ→θ[x,z,a]).
● Beispiel zur Visualisierung:

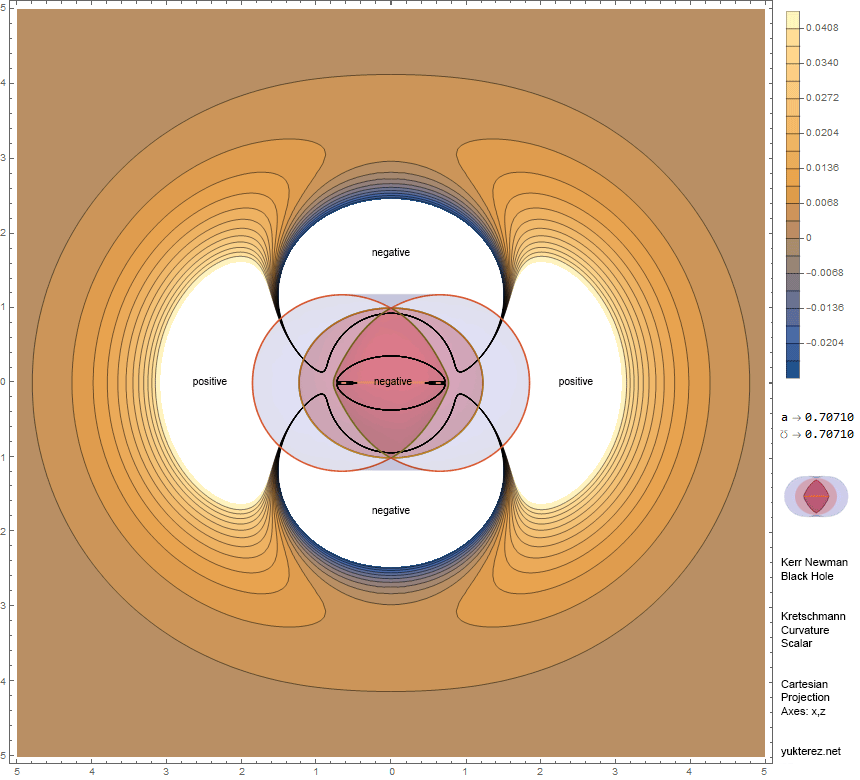
 In diesem Beispiel wird der Kretschmann Skalar für ein Kerr Newman SL bei y=0 auf die x,z-Ebene projiziert und mit den Horizonten und Ergosphären überblendet. Die schwarzen Kurven bezeichnen Flächen konstanter Krümmung; die geclippten Bereiche sind weiß markiert und je nachdem entweder stark positiv oder stark negativ gekrümmt. Gebündelte schwarze Kurven die weiße Flächen separieren sind harte Übergänge zwischen positiver und negativer Krümmung. Für andere Spin- und Ladungskombinationen wird auf das obere Bild geklickt, um die Animation einzuschalten klick hier. Für die Bahnen von bewegten Testpartikeln oder Photonen siehe ganz oben unter "verwandte Beiträge".
In diesem Beispiel wird der Kretschmann Skalar für ein Kerr Newman SL bei y=0 auf die x,z-Ebene projiziert und mit den Horizonten und Ergosphären überblendet. Die schwarzen Kurven bezeichnen Flächen konstanter Krümmung; die geclippten Bereiche sind weiß markiert und je nachdem entweder stark positiv oder stark negativ gekrümmt. Gebündelte schwarze Kurven die weiße Flächen separieren sind harte Übergänge zwischen positiver und negativer Krümmung. Für andere Spin- und Ladungskombinationen wird auf das obere Bild geklickt, um die Animation einzuschalten klick hier. Für die Bahnen von bewegten Testpartikeln oder Photonen siehe ganz oben unter "verwandte Beiträge".
● Benötigte Gleichungen und Regeln:

Feldgleichung in Abhängigkeit vom kovarianten Energie-Impuls-Tensor Tᵢⱼ (der ausgegraute Teil wird hier wo Λ als Vakuumenergie behandelt wird nicht benötigt da die dunkle Energiedichte im Energie/Impuls-Tensor ebenfalls als Energie verbucht wird; falls Λ nicht als Energieform sondern so wie Einstein es im Rahmen seines sogenannten biggest blunders gemeint hat behandelt wird wird der Term so wie in grau gezeigt subtrahiert sofern die +--- Signatur vorliegt, und bei -+++ addiert so dass die kosmologische Konstante nicht als Energiedichte in Tᵢⱼ einfließt):
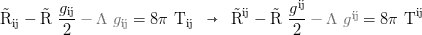

Riemann Tensor:
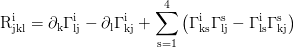
Ricci Tensor:
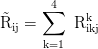
Ricci Skalar:
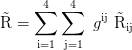
Kretschmann Skalar:
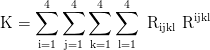
Einstein Tensor:
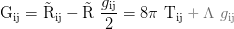
Kronecker Delta:
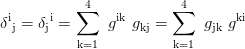
Christoffelsymbole zweiter Art:
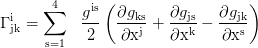
Intervall, Partikel: μ=-1, Photonen: μ=0:
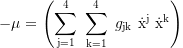
Maxwell Tensor mit dem Vektorpotential A:
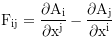

Erste Eigenzeitableitung und Impuls:
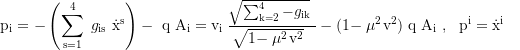
Totale Zeitdilatation und lokale Geschwindigkeit:
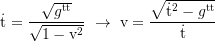
Geschwindigkeit der lokalen Referenzsysteme in die k-Richtung (relativ zu fixen Koordinaten):
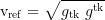
Zweite Eigenzeitableitung eines freien Partikels:
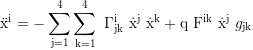
Eigenbeschleunigung (Kraft) eines nichtgeodätischen Partikels:
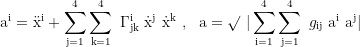
Paralleltransport eines Vektors V:
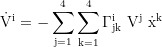

Indexverschieberegel:
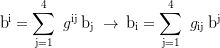
Mehrere Indizes:
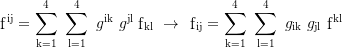
Kontraktion:
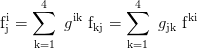
Gemischte Indizes:
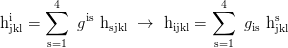

Transformation von einem Koordinatensystem x in ein anderes x̅:
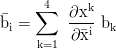
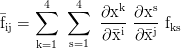

In diesem Beitrag werden natürliche Einheiten verwendet. Der Overdot steht für die Ableitung nach der Eigenzeit τ: ẋ=dx/dτ
● Empfohlene Tutorials:



Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* Mathematica Syntax | EINSTEIN-MAXWELL TENSOR+GEODESIC SOLVER | geodesics.yukterez.net *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
ClearAll["Local`*"]; LaunchKernels[4];
smp[y_]:=Simplify[y, Reals];
list[y_]:=y[[1]]==y[[2]];
rplc[y_]:=(((((((y/.t->t[τ])/.r->r[τ])/.θ->θ[τ])/.φ->φ[τ])/.Derivative[1][t[τ]]->
t'[τ])/.Derivative[1][r[τ]]->r'[τ])/.Derivative[1][θ[τ]]->θ'[τ])/.Derivative[1][φ[τ]]->φ'[τ]
(* kovariante metrische Komponenten *)
g11=gtt=-((-Δ+ж a^2 Sin[θ]^2)/(Σ χ^2));
g22=grr=-Σ/Δ;
g33=gθθ=-Σ/ж;
g44=gφφ=-((ж σ^2 Sin[θ]^2-a^2 Δ Sin[θ]^4)/(Σ χ^2));
g14=gtφ=-(( a (Δ-ж σ) Sin[θ]^2)/(Σ χ^2));
g12=g13=g23=g24=g34=0;
(* Abkürzungen *)
Σ=r^2+a^2 Cos[θ]^2;
Δ=(r^2+a^2)(1-Λ/3 r^2)-2 M r+℧^2;
Χ=(r^2+a^2)^2-a^2 Sin[θ]^2 Δ;
щ=(q ℧ r (a^2+r^2))/(Δ Σ);
χ=1+Λ/3 a^2;
ж=1+Λ/3 a^2 Cos[θ]^2;
σ=a^2+r^2;
(* Dimensionen, elektrische Ladung, Spin, Vakuumenergie, Masse *)
x={t, r, θ, φ}; n=4; Ω=℧; ℧=℧; a=a; Λ=Λ; M=1; c=1; G=1;
"Metrischer Tensor"
mt=smp[{
{g11, g12, g13, g14},
{g12, g22, g23, g24},
{g13, g23, g33, g34},
{g14, g24, g34, g44}
}];
Subscript["g", μσ] -> MatrixForm[mt]
it=smp[Inverse[mt]];
"g"^μσ -> MatrixForm[it]
mx=Table[smp[Sum[
it[[i, k]] mt[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["g", "μ", "σ"] -> MatrixForm[mx]
md=Det[mt]; "|g|" -> smp[md]
"Elektromagnetisches Vektorpotential"
A={Ω r/Σ/χ, 0, 0, -Ω r/Σ/χ Sin[θ]^2 a}; Subscript["A", μ]->smp[A]
"Maxwell Tensor"
F=ParallelTable[smp[((D[A[[j]], x[[k]]]-D[A[[k]], x[[j]]]))], {j, 1, n}, {k, 1, n}];
Subscript["F", μσ] -> MatrixForm[F]
f=smp[ParallelTable[Sum[
it[[i, k]] it[[j, l]] F[[k, l]],
{k, 1, n}, {l, 1, n}], {i, 1, n}, {j, 1, n}]];
"F"^μσ -> MatrixForm[f]
џ=ParallelTable[smp[Sum[
it[[i, k]] F[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["F", "μ", "σ"] -> MatrixForm[џ]
"Christoffelsymbole"
chr=ParallelTable[smp[(1/2)Sum[(it[[i, s]])
(D[mt[[s, j]], x[[k]]]+D[mt[[s, k]], x[[j]]] -D[mt[[j, k]], x[[s]]]), {s, 1, n}]],
{i, 1, n}, {j, 1, n}, {k, 1, n}];
crs=ParallelTable[If[UnsameQ[chr[[i, j, k]], 0],
{Subsuperscript["Γ", ToString[j] <> ToString[k], i] -> chr[[i, j, k]]}],
{i, 1, n}, {j, 1, n}, {k, 1, j}];
TableForm[DeleteCases[Flatten[crs], Null]]
"gemischter Riemann Tensor"
rmn=ParallelTable[smp[
D[chr[[i, j, l]], x[[k]]] - D[chr[[i, j, k]], x[[l]]] +
Sum[chr[[s, j, l]] chr[[i, k, s]] -
chr[[s, j, k]] chr[[i, l, s]],
{s, 1, n}]], {i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
rie=ParallelTable[If[UnsameQ[rmn[[i, j, k, l]], 0],
{Subsuperscript["R", ToString[j] <> ToString[k] <> ToString[l], i] -> rmn[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, k - 1}];
TableForm[DeleteCases[Flatten[rie], Null]]
(* kovarianter Riemann Tensor *)
rcv=ParallelTable[Sum[mt[[i, j]] rmn[[j, k, l, m]], {j, 1, n}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
(* kontravarianter Riemann Tensor *)
rcn=ParallelTable[Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] rcv[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, n}, {h, 1, n}, {o, 1, n}, {p, 1, n}];
"Ricci Tensor"
rcc=ParallelTable[smp[
Sum[rmn[[i, j, i, l]], {i, 1, n}]], {j, 1, n}, {l, 1, n}];
Subscript["Ř", μσ] -> MatrixForm[rcc]
ric=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] rcc[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"Ř"^μσ -> MatrixForm[ric]
rck=ParallelTable[smp[Sum[
it[[i, k]] rcc[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["Ř", "μ", "σ"] -> MatrixForm[rck]
"Ricci Skalar"
Ř=smp[ParallelSum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ř"->Ř
"Kretschmann Skalar"
krn= smp[ParallelSum[rcv[[i, j, k, l]] rcn[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
"K"->krn
"Weyl Tensor"
weyl1=smp[ParallelTable[
rcv[[i, j, k, l]] -
(rcc[[i, k]] mt[[j, l]] -
rcc[[i, l]] mt[[j, k]] +
rcc[[j, l]] mt[[i, k]] -
rcc[[j, k]] mt[[i, l]])/2 +
(mt[[i, k]] mt[[j, l]] -
mt[[i, l]] mt[[j, k]])/6 Ř,
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
Weyl1=ParallelTable[If[UnsameQ[weyl1[[i, j, k, l]], 0],
{Subscript["W",
ToString[i] <> ToString[j] <> ToString[k] <> ToString[l]] -> weyl1[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
weyl2=smp[ParallelTable[
Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] weyl1[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, n}, {h, 1, n}, {o, 1, n}, {p, 1, n}]];
Weyl2=ParallelTable[If[UnsameQ[weyl2[[i, j, k, l]], 0],
{"W"^(ToString[i] <> ToString[j] <> ToString[k] <> ToString[l]) -> weyl2[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
weyl3=ParallelTable[smp[Sum[
it[[i, m]] weyl1[[m, j, k, l]], {m, 1, n}]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
Weyl3=ParallelTable[If[UnsameQ[weyl3[[i, j, k, l]], 0],
{Subsuperscript["W", ToString[j] <> ToString[k] <> ToString[l], ToString[i]] ->
weyl3[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
TableForm[DeleteCases[Flatten[Weyl3], Null]]
"kontrahierter Weyl Tensor"
weyl4=ParallelTable[smp[
Sum[weyl3[[i, j, i, l]], {i, 1, n}]], {j, 1, n}, {l, 1, n}];
Subscript["Ŵ", μσ] -> MatrixForm[weyl4]
weyl5=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] weyl4[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"Ŵ"^μσ -> MatrixForm[weyl5]
weyl6=ParallelTable[smp[Sum[
it[[i, k]] weyl4[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["Ŵ", "μ", "σ"] -> MatrixForm[weyl6]
"Weyl Skalar"
Ŵ=smp[ParallelSum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ŵ"->Ŵ
"Einstein Tensor"
est=smp[rcc-Ř mt/2];
Subscript["G", μσ] -> MatrixForm[est]
ein=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] est[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"G"^μσ -> MatrixForm[ein]
esm=ParallelTable[smp[Sum[
it[[i, k]] est[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["G", "μ", "σ"] -> MatrixForm[esm]
"Stress Energie Impuls Tensor"
set=smp[(est (* -Λ mt *) )c^4/8/π/G];
Subscript["T", μσ] -> MatrixForm[set]
sei=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] set[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"T"^μσ -> MatrixForm[sei]
sem=ParallelTable[smp[Sum[
it[[i, k]] set[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["T", "μ", "σ"] -> MatrixForm[sem]
Ť = smp[Sum[it[[i, j]] set[[i, j]], {i, 1, n}, {j, 1, n}]]; "T" -> Ť
"Bewegungsgleichungen"
geo=ParallelTable[smp[-Sum[
chr[[i, j, k]] x[[j]]' x[[k]]'+q f[[i, k]] x[[j]]' mt[[j, k]],
{j, 1, n}, {k, 1, n}]], {i, 1, n}];
equ=ParallelTable[{x[[i]]''[τ]==smp[rplc[geo[[i]]]]}, {i, 1, n}];
geodesic1=equ[[1]][[1]]
geodesic2=equ[[2]][[1]]
geodesic3=equ[[3]][[1]]
geodesic4=equ[[4]][[1]]
"totale Zeitdilatation"
zd=Sum[mt[[μ, ν]] x[[μ]]' x[[ν]]', {μ, 1, n}, {ν, 1, n}];
ṫ=Quiet[rplc[smp[Normal[Solve[
-μ c^2==(zd/.t'->ť), ť]]]]];
Derivative[1][s][τ]^2 == "ds²/dτ² == -μ" == smp[rplc[zd]]
Derivative[1][t][τ]->ṫ[[1, 1, 2]]||ṫ[[2, 1, 2]]||rplc[Sqrt[it[[1, 1]]]]/Sqrt[1-μ^2 v[τ]^2/c^2]
"kovarianter Viererimpuls"
p[μ_]:=-(Sum[mt[[μ, ν]]*x[[ν]]', {ν, 1, n}]+q A[[μ]]);
pt[τ]->rplc[smp[p[1]]]
pr[τ]->rplc[smp[p[2]]]
pθ[τ]->rplc[smp[p[3]]]
pφ[τ]->rplc[smp[p[4]]]
"linearer 3er-Impuls"
ṕ[i_]:=rplc[smp[Sqrt[-Sum[mt[[i, k]] x[[i]]' x[[k]]',
{k, 1, n}]]]]-Sqrt[1-μ^2 v[τ]^2/c^2] q A[[i]];
ṕr[τ]->ṕ[2]
ṕθ[τ]->ṕ[3]
ṕφ[τ]->ṕ[4]
"lokale Geschwindigkeit"
V[x_]:=smp[Normal[Solve[vx Sqrt[Sum[-mt[[i, x]], {i, 2, 4}]]/Sqrt[1-
μ^2 v[τ]^2/c^2]-(1-μ^2 v[τ]^2/c^2) q A[[x]]==
p[x], vx]][[1, 1]]];
rplc[V[2]]/.vx->vr[τ]
rplc[V[3]]/.vx->vθ[τ]
rplc[V[4]]/.vx->vφ[τ]
Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* Mathematica Syntax | EINSTEIN-MAXWELL TENSOR+GEODESIC SOLVER | geodesics.yukterez.net *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
ClearAll["Local`*"]; LaunchKernels[4];
smp[y_]:=Simplify[y,
X\[Element]Reals&&Y\[Element]Reals&&Z\[Element]Reals&&a\[Element]Reals];
list[y_]:=y[[1]]==y[[2]];
rplc[y_]:=(((((((y/.t->t[τ])/.X->X[τ])/.Y->Y[τ])/.Z->Z[τ])/.Derivative[1][t[τ]]->
t'[τ])/.Derivative[1][X[τ]]->X'[τ])/.Derivative[1][Y[τ]]->Y'[τ])/.Derivative[1][Z[τ]]->Z'[τ]
(* kovariante metrische Komponenten *)
g11=gtt=(a^2 Z^2+r^2 (-2 M r+r^2+℧^2))/(r^4+a^2 Z^2);
g22=gXX=-((a^4 r^4+2 a^2 r^6+r^8+2 M r^5 X^2+4 a M r^4 X Y+2 a^2 M r^3 Y^2+a^6 Z^2+
2 a^4 r^2 Z^2+a^2 r^4 Z^2-r^2 (r X+a Y)^2 ℧^2)/((a^2+r^2)^2 (r^4+a^2 Z^2)));
g33=gYY=-((a^4 r^4+2 a^2 r^6+r^8+2 a^2 M r^3 X^2-4 a M r^4 X Y+2 M r^5 Y^2+a^6 Z^2+
2 a^4 r^2 Z^2+a^2 r^4 Z^2-r^2 (a X-r Y)^2 ℧^2)/((a^2+r^2)^2 (r^4+a^2 Z^2)));
g44=gZZ=-((r^4+2 M r Z^2+Z^2 (a-℧) (a+℧))/(r^4+a^2 Z^2));
g12=gtX=-((r^2 (r X+a Y) (2 M r-℧^2))/((a^2+r^2) (r^4+a^2 Z^2)));
g13=gtY=(r^2 (a X-r Y) (2 M r-℧^2))/((a^2+r^2) (r^4+a^2 Z^2));
g14=gtZ=(r Z (-2 M r+℧^2))/(r^4+a^2 Z^2);
g23=gXY=(r^2 (r X+a Y) (a X-r Y) (2 M r-℧^2))/((a^2+r^2)^2 (r^4+a^2 Z^2));
g24=gXZ=-((r (r X+a Y) Z (2 M r-℧^2))/((a^2+r^2) (r^4+a^2 Z^2)));
g34=gYZ=(r (a X-r Y) Z (2 M r-℧^2))/((a^2+r^2) (r^4+a^2 Z^2));
(* Dimensionen, elektrische Ladung, Spin, Vakuumenergie, Masse *)
x={t, X, Y, Z}; n=4; Ω=℧; ℧=0; a=0; Λ=0; M=0; c=1; G=1;
"Metrischer Tensor"
mt=smp[{
{g11, g12, g13, g14},
{g12, g22, g23, g24},
{g13, g23, g33, g34},
{g14, g24, g34, g44}
}];
Subscript["g", μσ] -> MatrixForm[mt]
it=smp[Inverse[mt]];
"g"^μσ -> MatrixForm[it]
mx=Table[smp[Sum[
it[[i, k]] mt[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["g", "μ", "σ"] -> MatrixForm[mx]
md=Det[mt]; "|g|" -> smp[md]
"r als Funktion von X,Y,Z"
r=smp[Sqrt[-a^2+X^2+Y^2+Z^2+Sqrt[(a^2-X^2-Y^2-Z^2)^2+4 a^2 Z^2]]/Sqrt[2]]; "r"->r
"Elektromagnetisches Vektorpotential"
A=℧ r^3/(r^4+a^2+Z^2){1,(r X+a Y)/(r^2+a^2),(r Y-a Z)/(r^2+a^2),Z/r};
Subscript["A", μ]->smp[A]
"Maxwell Tensor"
F=ParallelTable[smp[((D[A[[j]], x[[k]]]-D[A[[k]], x[[j]]]))], {j, 1, n}, {k, 1, n}];
Subscript["F", μσ] -> MatrixForm[F]
f=smp[ParallelTable[Sum[
it[[i, k]] it[[j, l]] F[[k, l]],
{k, 1, n}, {l, 1, n}], {i, 1, n}, {j, 1, n}]];
"F"^μσ -> MatrixForm[f]
џ=ParallelTable[smp[Sum[
it[[i, k]] F[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["F", "μ", "σ"] -> MatrixForm[џ]
"Christoffelsymbole"
chr=ParallelTable[smp[(1/2)Sum[(it[[i, s]])
(D[mt[[s, j]], x[[k]]]+D[mt[[s, k]], x[[j]]] -D[mt[[j, k]], x[[s]]]), {s, 1, n}]],
{i, 1, n}, {j, 1, n}, {k, 1, n}];
crs=ParallelTable[If[UnsameQ[chr[[i, j, k]], 0],
{Subsuperscript["Γ", ToString[j] <> ToString[k], i] -> chr[[i, j, k]]}],
{i, 1, n}, {j, 1, n}, {k, 1, j}];
TableForm[DeleteCases[Flatten[crs], Null]]
"gemischter Riemann Tensor"
rmn=ParallelTable[smp[
D[chr[[i, j, l]], x[[k]]] - D[chr[[i, j, k]], x[[l]]] +
Sum[chr[[s, j, l]] chr[[i, k, s]] -
chr[[s, j, k]] chr[[i, l, s]],
{s, 1, n}]], {i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
rie=ParallelTable[If[UnsameQ[rmn[[i, j, k, l]], 0],
{Subsuperscript["R", ToString[j] <> ToString[k] <> ToString[l], i] -> rmn[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, k - 1}];
TableForm[DeleteCases[Flatten[rie], Null]]
(* kovarianter Riemann Tensor *)
rcv=ParallelTable[Sum[mt[[i, j]] rmn[[j, k, l, m]], {j, 1, n}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
(* kontravarianter Riemann Tensor *)
rcn=ParallelTable[Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] rcv[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, n}, {h, 1, n}, {o, 1, n}, {p, 1, n}];
"Ricci Tensor"
rcc=ParallelTable[smp[
Sum[rmn[[i, j, i, l]], {i, 1, n}]], {j, 1, n}, {l, 1, n}];
Subscript["Ř", μσ] -> MatrixForm[rcc]
ric=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] rcc[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"Ř"^μσ -> MatrixForm[ric]
rck=ParallelTable[smp[Sum[
it[[i, k]] rcc[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["Ř", "μ", "σ"] -> MatrixForm[rck]
"Ricci Skalar"
Ř=smp[ParallelSum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ř"->Ř
"Kretschmann Skalar"
krn= smp[ParallelSum[rcv[[i, j, k, l]] rcn[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
"K"->krn
"Weyl Tensor"
weyl1=smp[ParallelTable[
rcv[[i, j, k, l]] -
(rcc[[i, k]] mt[[j, l]] -
rcc[[i, l]] mt[[j, k]] +
rcc[[j, l]] mt[[i, k]] -
rcc[[j, k]] mt[[i, l]])/2 +
(mt[[i, k]] mt[[j, l]] -
mt[[i, l]] mt[[j, k]])/6 Ř,
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}]];
Weyl1=ParallelTable[If[UnsameQ[weyl1[[i, j, k, l]], 0],
{Subscript["W",
ToString[i] <> ToString[j] <> ToString[k] <> ToString[l]] -> weyl1[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
weyl2=smp[ParallelTable[
Sum[it[[m, i]] it[[h, j]] it[[o, k]] it[[p, l]] weyl1[[i, j, k, l]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}],
{m, 1, n}, {h, 1, n}, {o, 1, n}, {p, 1, n}]];
Weyl2=ParallelTable[If[UnsameQ[weyl2[[i, j, k, l]], 0],
{"W"^(ToString[i] <> ToString[j] <> ToString[k] <> ToString[l]) -> weyl2[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
weyl3=ParallelTable[smp[Sum[
it[[i, m]] weyl1[[m, j, k, l]], {m, 1, n}]],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
Weyl3=ParallelTable[If[UnsameQ[weyl3[[i, j, k, l]], 0],
{Subsuperscript["W", ToString[j] <> ToString[k] <> ToString[l], ToString[i]] ->
weyl3[[i, j, k, l]]}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}];
TableForm[DeleteCases[Flatten[Weyl3], Null]]
"kontrahierter Weyl Tensor"
weyl4=ParallelTable[smp[
Sum[weyl3[[i, j, i, l]], {i, 1, n}]], {j, 1, n}, {l, 1, n}];
Subscript["Ŵ", μσ] -> MatrixForm[weyl4]
weyl5=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] weyl4[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"Ŵ"^μσ -> MatrixForm[weyl5]
weyl6=ParallelTable[smp[Sum[
it[[i, k]] weyl4[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["Ŵ", "μ", "σ"] -> MatrixForm[weyl6]
"Weyl Skalar"
Ŵ=smp[ParallelSum[it[[i, j]] rcc[[i, j]], {i, 1, n}, {j, 1, n}]]; "Ŵ"->Ŵ
"Einstein Tensor"
est=smp[rcc-Ř mt/2];
Subscript["G", μσ] -> MatrixForm[est]
ein=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] est[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"G"^μσ -> MatrixForm[ein]
esm=ParallelTable[smp[Sum[
it[[i, k]] est[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["G", "μ", "σ"] -> MatrixForm[esm]
"Stress Energie Impuls Tensor"
set=smp[(est (* -Λ mt *) )c^4/8/π/G];
Subscript["T", μσ] -> MatrixForm[set]
sei=ParallelTable[smp[Sum[
it[[i, k]] it[[j, l]] set[[k, l]], {k, 1, n}, {l, 1, n}]],
{i, 1, n}, {j, 1, n}];
"T"^μσ -> MatrixForm[sei]
sem=ParallelTable[smp[Sum[
it[[i, k]] set[[k, j]], {k, 1, n}]],
{i, 1, n}, {j, 1, n}];
Subsuperscript["T", "μ", "σ"] -> MatrixForm[sem]
Ť = smp[Sum[it[[i, j]] set[[i, j]], {i, 1, n}, {j, 1, n}]]; "T" -> Ť
"Bewegungsgleichungen"
geo=ParallelTable[smp[-Sum[
chr[[i, j, k]] x[[j]]' x[[k]]'+q f[[i, k]] x[[j]]' mt[[j, k]],
{j, 1, n}, {k, 1, n}]], {i, 1, n}];
equ=ParallelTable[{x[[i]]''[τ]==smp[rplc[geo[[i]]]]}, {i, 1, n}];
geodesic1=equ[[1]][[1]]
geodesic2=equ[[2]][[1]]
geodesic3=equ[[3]][[1]]
geodesic4=equ[[4]][[1]]
"totale Zeitdilatation"
zd=Sum[mt[[μ, ν]] x[[μ]]' x[[ν]]', {μ, 1, n}, {ν, 1, n}];
ṫ=Quiet[rplc[smp[Normal[Solve[
-μ c^2==(zd/.t'->ť), ť]]]]];
Derivative[1][s][τ]^2 == "ds²/dτ² == -μ" == smp[rplc[zd]]
Derivative[1][t][τ]->ṫ[[1, 1, 2]]||ṫ[[2, 1, 2]]||rplc[Sqrt[it[[1, 1]]]]/Sqrt[1-μ^2 v[τ]^2/c^2]
"kovarianter Viererimpuls"
p[μ_]:=-(Sum[mt[[μ, ν]]*x[[ν]]', {ν, 1, n}]+q A[[μ]]);
pt[τ]->rplc[smp[p[1]]]
pX[τ]->rplc[smp[p[2]]]
pY[τ]->rplc[smp[p[3]]]
pZ[τ]->rplc[smp[p[4]]]
"linearer 3er-Impuls"
ṕ[i_]:=rplc[smp[Sqrt[-Sum[mt[[i, k]] x[[i]]' x[[k]]',
{k, 1, n}]]]]-Sqrt[1-μ^2 v[τ]^2/c^2] q A[[i]];
ṕX[τ]->ṕ[2]
ṕY[τ]->ṕ[3]
ṕZ[τ]->ṕ[4]
"lokale Geschwindigkeit"
V[x_]:=smp[Normal[Solve[vx Sqrt[Sum[-mt[[i, x]], {i, 2, 4}]]/Sqrt[1-
μ^2 v[τ]^2/c^2]-(1-μ^2 v[τ]^2/c^2) q A[[x]]==
p[x], vx]][[1, 1]]]; ν[i_]:=rplc[smp[Sqrt[-Sum[mt[[i, k]] x[[i]]' x[[k]]', {k, 1, n}]]]]/γ;
rplc[V[2]]/.vx->vX[τ]
rplc[V[3]]/.vx->vY[τ]
rplc[V[4]]/.vx->vZ[τ]
 Der obere Solver ist mit der KNdS-Metrik in {t,r,θ,φ}-BL-Koordinaten voreingestellt. Mit Λ=0 reduziert sich die Metrik auf Kerr Newman, mit Λ=℧=0 auf Kerr, mit Λ=a=0 auf Reissner Nordström, mit Λ=℧=a=0 auf Schwarzschild, mit ℧=a=0 auf Schwarzschild De Sitter, mit ℧=a=M=0 auf De Sitter und mit Λ=℧=a=M=0 auf Minkowski. Der untere Solver ist auf die Kerr Newman Metrik in kartesischen Kerr Schild Koordinaten eingestellt (da die Metrik in diesen Koordinaten sehr kompliziert wird benötigt dieser sehr viel mehr Rechenzeit). Falls das Linienelement in einer unübersichtlichen Form vorliegt können die metrischen Koeffizienten mit dem Linienelementzerleger sauber getrennt und hernach in den Solver eingegeben werden.
Der obere Solver ist mit der KNdS-Metrik in {t,r,θ,φ}-BL-Koordinaten voreingestellt. Mit Λ=0 reduziert sich die Metrik auf Kerr Newman, mit Λ=℧=0 auf Kerr, mit Λ=a=0 auf Reissner Nordström, mit Λ=℧=a=0 auf Schwarzschild, mit ℧=a=0 auf Schwarzschild De Sitter, mit ℧=a=M=0 auf De Sitter und mit Λ=℧=a=M=0 auf Minkowski. Der untere Solver ist auf die Kerr Newman Metrik in kartesischen Kerr Schild Koordinaten eingestellt (da die Metrik in diesen Koordinaten sehr kompliziert wird benötigt dieser sehr viel mehr Rechenzeit). Falls das Linienelement in einer unübersichtlichen Form vorliegt können die metrischen Koeffizienten mit dem Linienelementzerleger sauber getrennt und hernach in den Solver eingegeben werden.
● Beispiele verschiedener Metriken in unterschiedlichen Koordinaten:

 Boyer Lindquist ist das rotierende Äquivalent zu Droste (Koordinatenzeit eines stationären feldfreien Beobachters), Kerr-Schild zu Finkelstein (Koordinatenzeit wird per einfallenden Lichtstrahlen aufgestempelt) und Doran zu Raindrop Koordinaten (t wird durch mit der negativen Fluchtgeschwindigkeit freifallende Uhren definiert). In den Bewegungsgleichungen sind die Koordinaten Funktionen der Eigenzeit bzw. bei Photonen des affinen Parameters (t→t[τ], r'→r'[τ], θ''→θ''[τ] usw), in manchen Beispielen mit kilometerlangem Output wird dies der Kürze wegen und da es sich sowieso aus dem Zusammenhang ergibt nicht extra angeschrieben (die rplc Funktion ist dann deaktiviert, im Code ist sie jedoch standardmäßig aktiviert damit der Output bei Bedarf gleich direkt in den Simulator übertragen werden kann). Sofern nicht anders angegeben werden natürliche Einheiten mit G=M=c=K=1 verwendet (Längen haben die Einheit GM/c², Zeiten GM/c³, Geschwindigkeiten c, etc). Der einheitsbehaftete Wert der kosmologischen Konstante ist in unserem Universum Λ=1.1056e-52/m² (im Kontext eines schwarzen Lochs mit M=1e40kg wäre das dimensionslos Λ→G²M²Λ/c⁴=6.0963e-87), wobei die Vakuumdichte ρΛ=c²Λ/(8πG) beträgt.
Boyer Lindquist ist das rotierende Äquivalent zu Droste (Koordinatenzeit eines stationären feldfreien Beobachters), Kerr-Schild zu Finkelstein (Koordinatenzeit wird per einfallenden Lichtstrahlen aufgestempelt) und Doran zu Raindrop Koordinaten (t wird durch mit der negativen Fluchtgeschwindigkeit freifallende Uhren definiert). In den Bewegungsgleichungen sind die Koordinaten Funktionen der Eigenzeit bzw. bei Photonen des affinen Parameters (t→t[τ], r'→r'[τ], θ''→θ''[τ] usw), in manchen Beispielen mit kilometerlangem Output wird dies der Kürze wegen und da es sich sowieso aus dem Zusammenhang ergibt nicht extra angeschrieben (die rplc Funktion ist dann deaktiviert, im Code ist sie jedoch standardmäßig aktiviert damit der Output bei Bedarf gleich direkt in den Simulator übertragen werden kann). Sofern nicht anders angegeben werden natürliche Einheiten mit G=M=c=K=1 verwendet (Längen haben die Einheit GM/c², Zeiten GM/c³, Geschwindigkeiten c, etc). Der einheitsbehaftete Wert der kosmologischen Konstante ist in unserem Universum Λ=1.1056e-52/m² (im Kontext eines schwarzen Lochs mit M=1e40kg wäre das dimensionslos Λ→G²M²Λ/c⁴=6.0963e-87), wobei die Vakuumdichte ρΛ=c²Λ/(8πG) beträgt.
● Koordinatentransformator:

Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||||| KOORDINATEN TRANSFORMATOR | geodesics.yukterez.net | Droste -> Finkelstein ||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
d1={dt, dr, dθ, dφ};
d2={dT, dr, dθ, dφ};
n=4;
"Schwarzschild, Droste"
g11=gtt=1-2M/r;
g22=grr=-1/gtt;
g33=gθθ=-r^2;
g44=gφφ=-r^2 Sin[θ]^2;
g12=g13=g14=g23=g24=g34=0;
m1={
{g11, g12, g13, g14},
{g12, g22, g23, g24},
{g13, g23, g33, g34},
{g14, g24, g34, g44}};
A1={0, 0, 0, 0};
Subscript["A", μ] -> A1
M1=MatrixForm[m1];
Subscript["g", μσ] -> M1
"Schwarzschild, Finkelstein"
v=-2M/r;
dt=dT+v/gtt dr ;
m2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] D[d1[[s]], d2[[j]]] m1[[k, s]],
{k, 1, n}, {s, 1, n}], {i, 1, n}, {j, 1, n}]];
M2=MatrixForm[m2];
Subscript["g", μσ] -> M2
A2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] A1[[k]],
{k, 1, n}], {i, 1, n}]];
Subscript["A", μ] -> A2
Quit[]
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||| KOORDINATEN TRANSFORMATOR | geodesics.yukterez.net | Sphärisch -> Kartesisch |||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
d1={dt, dr, dθ, dΦ};
d2={dt, dX, dY, dZ};
n=4;
"Schwarzschild, Droste, Sphärisch"
g11=gtt=1-2/r;
g22=gXX=-1/g11;
g33=gYY=-r^2;
g44=gZZ=-r^2 Sin[θ]^2;
g12=gtX=0;
g13=gtY=0;
g14=gtZ=0;
g23=gXY=0;
g24=gXZ=0;
g34=gYZ=0;
m1={
{g11, g12, g13, g14},
{g12, g22, g23, g24},
{g13, g23, g33, g34},
{g14, g24, g34, g44}};
M1=MatrixForm[m1];
Subscript["g", μσ] -> M1
A1={0, 0, 0, 0};
Subscript["A", μ] -> A1
"Schwarzschild, Droste, Kartesisch"
dr=(X dX+Y dY+Z dZ)/r;
dθ=(Z X dX+Z Y dY-(X^2+Y^2) dZ)/r^2/Sqrt[X^2+Y^2];
dΦ=(X dY-Y dX)/(X^2+Y^2);
r=Sqrt[X^2+Y^2+Z^2];
θ=ArcTan[Z, Sqrt[X^2+Y^2]];
m2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] D[d1[[s]], d2[[j]]] m1[[k, s]],
{k, 1, n}, {s, 1, n}], {i, 1, n}, {j, 1, n}]];
M2=MatrixForm[m2];
Subscript["g", μσ] -> M2
A2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] A1[[k]],
{k, 1, n}], {i, 1, n}]];
Subscript["A", μ] -> A2
Quit[]
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* || KOORDINATEN TRANSFORMATOR | geodesics.yukterez.net | Boyer Lindquist -> Raindrop || *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
d1={dt, dr, dθ, dΦ};
d2={dT, dr, dθ, dφ};
n=4;
"Kerr Newman, Boyer Lindquist"
g11=gtt=-(2r-r^2-℧^2-a^2+a^2 Sin[θ]^2)/(r^2+a^2 Cos[θ]^2);
g22=grr=-(r^2+a^2 Cos[θ]^2)/(a^2-2r+r^2+℧^2);
g33=gθθ=-r^2-a^2 Cos[θ]^2;
g44=gφφ=-((a^2+r^2)^2 Sin[θ]^2-a^2 (a^2-2r+r^2+℧^2) Sin[θ]^4)/(r^2+a^2 Cos[θ]^2);
g14=gtφ=-(a (℧^2-2r) Sin[θ]^2)/(r^2+a^2 Cos[θ]^2);
g12=g13=g23=g24=g34=0;
m1={
{g11, g12, g13, g14},
{g12, g22, g23, g24},
{g13, g23, g33, g34},
{g14, g24, g34, g44}};
M1=MatrixForm[m1];
Subscript["g", μσ] -> M1
A1={r ℧/(r^2+a^2 Cos[θ]^2), 0, 0, -a r ℧ Sin[θ]^2/(r^2+a^2 Cos[θ]^2)};
Subscript["A", μ] -> A1
"Kerr Newman, Raindrop"
σ=+a^2+r^2;
v=-Sqrt[2r-℧^2]/Sqrt[σ];
dt=+dT+v dr/(1-v^2);
dΦ=+dφ+a v dr/σ/(1-v^2);
m2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] D[d1[[s]], d2[[j]]] m1[[k, s]],
{k, 1, n}, {s, 1, n}], {i, 1, n}, {j, 1, n}]];
M2=MatrixForm[m2];
Subscript["g", μσ] -> M2
A2=FullSimplify[Table[Sum[D[d1[[k]], d2[[i]]] A1[[k]],
{k, 1, n}], {i, 1, n}]];
Subscript["A", μ] -> A2
 Transformation von einem Koordinatensystem in ein anderes. Input: vorhandene kovariante Metrik und Transformationsregel für die Koordinaten, Output: neue kovariante Metrik (für die praktische Anwendung siehe das Beispiel unten).
Transformation von einem Koordinatensystem in ein anderes. Input: vorhandene kovariante Metrik und Transformationsregel für die Koordinaten, Output: neue kovariante Metrik (für die praktische Anwendung siehe das Beispiel unten).
● Beispiel zur Koordinatentransformation:


 oben: Transformationsregel, unten: Transformation
oben: Transformationsregel, unten: Transformation
 Beispiel zum Koordinatentransformator: Eingabe der Schwarzschild Metrik in kovarianten Droste Bookkeeper Koordinaten (links) und der Transformationsregel dτ=dt-v·dr/gₜₜ, Ausgabe: Schwarzschild Metrik in kovarianten Gullstrand Painlevé (Raindrop) Koordinaten (rechts). Für die Rücktransformation klick aufs Bild. Äquivalente Transformation für die Kerr Newman Metrik (Boyer Lindquist zu Doran): klick.
Beispiel zum Koordinatentransformator: Eingabe der Schwarzschild Metrik in kovarianten Droste Bookkeeper Koordinaten (links) und der Transformationsregel dτ=dt-v·dr/gₜₜ, Ausgabe: Schwarzschild Metrik in kovarianten Gullstrand Painlevé (Raindrop) Koordinaten (rechts). Für die Rücktransformation klick aufs Bild. Äquivalente Transformation für die Kerr Newman Metrik (Boyer Lindquist zu Doran): klick.
● Funktionsplotter:

Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* | Mathematica Syntax | EINSTEIN PLOTTER | geodesics.yukterez.net | Version 10.1.2020 | *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* Kartesisch zu Boyer Lindquist *)
k[x_, z_, a_]:=FindInstance[x==Sqrt[R^2+a^2]Sin[u]&&z==R Cos[u]&&u<2Pi&&u>=0&&R>=0, {R, u}, Reals]
r[x_, z_, a_]:=k[x, z, a][[1, 1, 2]];
θ[x_, z_, a_]:=k[x, z, a][[1, 2, 2]];
(* Kretschmann Skalar *)
K[x_, z_, a_, ℧_]:=-(1/((a^2+a^2 Cos[2 θ[x, z, a]]+2 r[x, z, a]^2)^6))32 (30 a^6-42 a^4 ℧^4+3 a^6 Cos[6 θ[x, z, a]]+360 a^4 ℧^2 r[x, z, a]-540 a^4 r[x, z, a]^2+272 a^2 ℧^4 r[x, z, a]^2-960 a^2 ℧^2 r[x, z, a]^3+720 a^2 r[x, z, a]^4-112 ℧^4 r[x, z, a]^4+192 ℧^2 r[x, z, a]^5-96 r[x, z, a]^6+2 a^4 Cos[4 θ[x, z, a]] (9 a^2-7 ℧^4+60 ℧^2 r[x, z, a]-90 r[x, z, a]^2)+a^2 Cos[2 θ[x, z, a]] (45 a^4+16 r[x, z, a]^2 (17 ℧^4-60 ℧^2 r[x, z, a]+45 r[x, z, a]^2)-8 a^2 (7 ℧^4-60 ℧^2 r[x, z, a]+90 r[x, z, a]^2)));
(* Horizonte und Ergosphären *)
rE=1+Sqrt[1-a^2 Cos[Θ]^2-a^2];(*äußere Ergosphäre*)
RE={Sqrt[rE^2+a^2] Sin[Θ], rE Cos[Θ]};
rG=1-Sqrt[1-a^2 Cos[Θ]^2-a^2];(*innere Ergosphäre*)
RG={Sqrt[rG^2+a^2] Sin[Θ], rG Cos[Θ]};
rA=1+Sqrt[1-a^2-a^2];(*äußerer Horizont*)
RA={Sqrt[rA^2+a^2] Sin[Θ], rA Cos[Θ]};
rI=1-Sqrt[1-a^2-a^2];(*innerer Horizont*)
RI={Sqrt[rI^2+a^2] Sin[Θ], rI Cos[Θ]};
(* Kartesischer Plot *)
℧=a;
Do[Print[Rasterize[Grid[{{
Show[
ContourPlot[K[x, z, a, ℧], {x, 0, 5}, {z, 0, 5}, PlotLegends->Automatic, Contours->20, ContourShading->Automatic, MaxRecursion->3, ImageSize->400],
ParametricPlot[{RI, RA, RG, RE}, {Θ, 0, Pi/2}, Frame->False]
]}, {"a"->N@a}, {"℧"->N@℧},
{" "}},
Alignment->Left]]],
{a, 0, Sqrt[1/2], Sqrt[1/2]/2}]
 Der Plotter ist auf einen Konturplot des Kretschmann Skalars für die Kerr Newman Metrik eingestellt. Andere Funktionen können aus dem Solver kopiert und eingesetzt werden, wobei bei der Projektion auf die x,z-Ebene die r,θ-Koordinaten als Funktionen von x,z angeschrieben gehören (r→r[x,z,a], θ→θ[x,z,a]).
Der Plotter ist auf einen Konturplot des Kretschmann Skalars für die Kerr Newman Metrik eingestellt. Andere Funktionen können aus dem Solver kopiert und eingesetzt werden, wobei bei der Projektion auf die x,z-Ebene die r,θ-Koordinaten als Funktionen von x,z angeschrieben gehören (r→r[x,z,a], θ→θ[x,z,a]).
● Beispiel zur Visualisierung:


 In diesem Beispiel wird der Kretschmann Skalar für ein Kerr Newman SL bei y=0 auf die x,z-Ebene projiziert und mit den Horizonten und Ergosphären überblendet. Die schwarzen Kurven bezeichnen Flächen konstanter Krümmung; die geclippten Bereiche sind weiß markiert und je nachdem entweder stark positiv oder stark negativ gekrümmt. Gebündelte schwarze Kurven die weiße Flächen separieren sind harte Übergänge zwischen positiver und negativer Krümmung. Für andere Spin- und Ladungskombinationen wird auf das obere Bild geklickt, um die Animation einzuschalten klick hier. Für die Bahnen von bewegten Testpartikeln oder Photonen siehe ganz oben unter "verwandte Beiträge".
In diesem Beispiel wird der Kretschmann Skalar für ein Kerr Newman SL bei y=0 auf die x,z-Ebene projiziert und mit den Horizonten und Ergosphären überblendet. Die schwarzen Kurven bezeichnen Flächen konstanter Krümmung; die geclippten Bereiche sind weiß markiert und je nachdem entweder stark positiv oder stark negativ gekrümmt. Gebündelte schwarze Kurven die weiße Flächen separieren sind harte Übergänge zwischen positiver und negativer Krümmung. Für andere Spin- und Ladungskombinationen wird auf das obere Bild geklickt, um die Animation einzuschalten klick hier. Für die Bahnen von bewegten Testpartikeln oder Photonen siehe ganz oben unter "verwandte Beiträge".
● Benötigte Gleichungen und Regeln:

Feldgleichung in Abhängigkeit vom kovarianten Energie-Impuls-Tensor Tᵢⱼ (der ausgegraute Teil wird hier wo Λ als Vakuumenergie behandelt wird nicht benötigt da die dunkle Energiedichte im Energie/Impuls-Tensor ebenfalls als Energie verbucht wird; falls Λ nicht als Energieform sondern so wie Einstein es im Rahmen seines sogenannten biggest blunders gemeint hat behandelt wird wird der Term so wie in grau gezeigt subtrahiert sofern die +--- Signatur vorliegt, und bei -+++ addiert so dass die kosmologische Konstante nicht als Energiedichte in Tᵢⱼ einfließt):
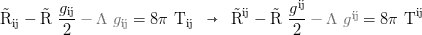

Riemann Tensor:
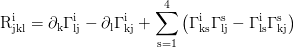
Ricci Tensor:
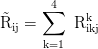
Ricci Skalar:
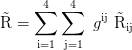
Kretschmann Skalar:
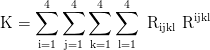
Einstein Tensor:
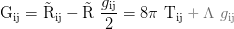
Kronecker Delta:
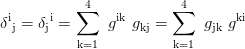
Christoffelsymbole zweiter Art:
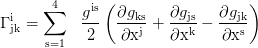
Intervall, Partikel: μ=-1, Photonen: μ=0:
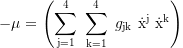
Maxwell Tensor mit dem Vektorpotential A:
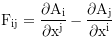

Erste Eigenzeitableitung und Impuls:
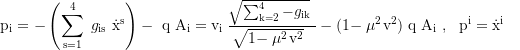
Totale Zeitdilatation und lokale Geschwindigkeit:
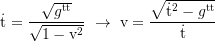
Geschwindigkeit der lokalen Referenzsysteme in die k-Richtung (relativ zu fixen Koordinaten):
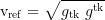
Zweite Eigenzeitableitung eines freien Partikels:
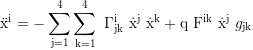
Eigenbeschleunigung (Kraft) eines nichtgeodätischen Partikels:
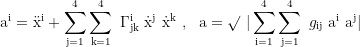
Paralleltransport eines Vektors V:
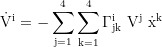

Indexverschieberegel:
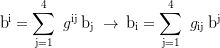
Mehrere Indizes:
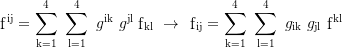
Kontraktion:
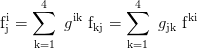
Gemischte Indizes:
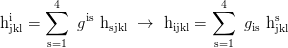

Transformation von einem Koordinatensystem x in ein anderes x̅:
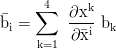
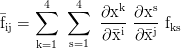

In diesem Beitrag werden natürliche Einheiten verwendet. Der Overdot steht für die Ableitung nach der Eigenzeit τ: ẋ=dx/dτ

● Empfohlene Tutorials:

- Text:
- Standard Reference: Bertschinger (1993)
- Standard Reference: Stefani et al (2003)
- Standard Reference: MTW (1973)
- Tutorial: Hartle (2004)
Video: - Playlist: Neil Turok (2017)
- Playlist: Paul Wagner (2018)
- Playlist: Jörn Loviscach (2016)
- Playlist: Einstein Toolkit (2017)
- Playlist: Leonard Susskind (2012)
- Playlist: Frederic Schuller (2015)
- Playlist: Eugene Khutoryansky (2017)
- Playlist: Emil Akhmenov (2016)
- Playlist: Science Clic (2020)
- Playlist: Trin Tragula (2017)
- Playlist: Eigenchris (2020)


