Relativistischer Raytracer

[Yukterez]

Kerr Newman || Kerr || Reissner Nordström || Schwarzschild || Feldgleichungen || Flamm || Gravitationslinsen || Projektionen || Kartographie
Das ist die deutschsprachige Version.   English versions will be available on en.yukterez.net and yukipedia.   Last update: 9.9.2020

Simulator in Boyer Lindquist Koordinaten: die Geschwindigkeit des Beobachters wird relativ zum lokalen ZAMO eingegeben; ein negatives vr steht für eine radiale Bewegung auf das schwarze Loch zu und ein positives von ihm weg, ein positives vφ für eine prograde und ein negatives für eine retrograde, und ein positives vθ im Bereich φ=-π/2..+π/2 für eine Bewegung in Richtung Südpol, und ein negatives in Richtung Nordpol. Output: gravitationsgelinstes Abbild einer starren (die weißen Hilfslinien stehen für konstante r und φ) und einer dynamisch rotierenden (die radialen Hilfslinien werden entsprechend der lokalen Frame Dragging Geschwindigkeit und der Lichtlaufzeit zum Beobachter verquirlt) Akkretionsscheibe (sowohl als Composite als auch der einzelnen Lichtechos), gravitationsgelinster Sternenhintergrund, Abbild einer knapp über dem Horizont aufgespannten und korotierenden Schale, Frequenzverschiebung von Scheibe und Hintergrund, Konturen des Schattens:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* > raytracing.yukterez.net | 07.04.2018 - 29.04.2023 | Version 21 | Simon Tyran, Vienna *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
Pause[1]                                                   (* Boyer Lindquist Koordinaten *)
 
wp  = MachinePrecision;
mt0 = Automatic;
mt1 = {"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mta = mt0;                                (* mt0 für Geschwindigkeit, mt1 für Genauigkeit *)
 
kernels = 6;                                                          (* Parallelisierung *)
grain   = 5;                            (* Subparallelisierung auf kernels*grain Streifen *)
rsp     = "Nearest";                                                        (* Resampling *)
 
breite  = 240;                                               (* Zielabmessungen in Pixeln *)
hoehe   = 120;          (* Höhe sollte ein ganzzahliges Vielfaches von kernels*grain sein *)
zoom    = 1;                                  (* doppelter Zoom ergibt halben Sichtwinkel *)
 
LaunchKernels[kernels]
wp = MachinePrecision;                                                     (* Genauigkeit *)
st = 0.01;                                                    (* Auflösung des Gradienten *)
 
pic1 = Import["http://www.yukterez.net/mw/1/flip70.png"];    (* Hintergrundpanorama laden *)
pic2 = Import["http://www.yukterez.net/mw/1/worldmap.png"];    (* Sphärenoberfläche laden *)
pic3 = Import["http://www.yukterez.net/mw/akkretionsscheibe.jpg"];(* Scheibentextur laden *)
pic4 = Import["http://www.yukterez.net/mw/disk.png"];          (* Scheibengeometrie laden *)
pic5 = Import["http://www.yukterez.net/mw/gradient1.png"];   (* Helligkeitsgradient laden *)
pic6 = Import["http://www.yukterez.net/mw/gradient2.png"];          (* Farbgradient laden *)
pic7 = Import["http://www.yukterez.net/mw/1/cl.png"];               (* Checkerboard laden *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 1) Startbedingungen und Position des Beobachters ||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 10;                                              (* Radialkoordinate des Beobachters *)
R0 = 500;                                (* Radius des umspannenden Kugelschalenpanoramas *)
R1 = Max[1, Re[1.0001 rA]];                                                     (* Sphäre *)
rT = 10;                                                 (* Lichtlaufzeit Synchronisation *)
t0 = 0;                                                      (* Eigenzeit des Beobachters *)
 
si = isco+0.1;                                           (* Akkretionsscheibe Innenradius *)
sr = 7;                                                  (* Akkretionsscheibe Außenradius *)
θj = 10 π/180;                                                   (* Jet Winkeldurchmesser *)
 
θ0 = 70 π/180;                                                             (* Breitengrad *)
φ0 = 0;                                                                     (* Längengrad *)
 
tmax = -100 R0;                                         (* zeitlicher Integrationsbereich *)
 
a  = 0.7;                                                                (* Spinparameter *)
℧  = 0.7;                                       (* spezifische Ladung des schwarzen Lochs *)
v0 = 1;                                                   (* Geschwindigkeit der Photonen *)
q  = 0;                                                            (* Ladung der Photonen *)
 
vr = -vя;                                      (* Radiale Geschwindigkeit des Beobachters *)
vϑ = 0;                                         (* Polare Geschwindigkeit des Beobachters *)
vφ = 0;       (* Azimutale Geschwindigkeit des Beobachters: 0 für ZAMO, -й0 für stationär *)

vL = Sqrt[vr^2+vϑ^2+vφ^2];
 
hvs  = 0; (* ArcSin[vφ/vL] *)                        (* horizontaler Versatz in Radianten *)
vvs  = 0; (* ArcSin[vϑ/vL] *)                          (* vertikaler Versatz in Radianten *)

fmax = 2; fmin = 0;                                            (* Doppler Frequenzbereich *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 2) Bildreflektion |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
fpt[{x_, y_}] := {If[y<0, x+1, x], If[y<0, -y, y]}
 
pcr1 = ParallelTable[
ImageTransformation[pic1, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct1 = ImageAssemble[Table[{pcr1[[x]]}, {x, 2 kernels, 1, -1}]];
 
pcr2 = ParallelTable[
ImageTransformation[pic2, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct2 = ImageAssemble[Table[{pcr2[[x]]}, {x, 2 kernels, 1, -1}]];
 
pcr3 = ParallelTable[
ImageTransformation[pic7, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct3 = ImageAssemble[Table[{pcr3[[x]]}, {x, 2 kernels, 1, -1}]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 3) Funktionen |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
gtt = (2r0-℧^2)/Σ-1;
grr = Σ/Δ;
gθθ = Σ;
gφφ = Χ/Σ Sin[θ0]^2;
gtφ =-a (2r0-℧^2) Sin[θ0]^2/Σ;

rA = 1+Sqrt[1-a^2-℧^2];
rE = 1+Sqrt[1-℧^2];
 
Σ = r0^2+a^2 Cos[θ0]^2;
Δ = r0^2-2 r0+a^2+℧^2;
Χ = (r0^2+a^2)^2-a^2 Sin[θ0]^2 Δ;
 
Σs[rs_] := rs^2;
Δs[rs_] := rs^2-2 rs+a^2+℧^2;
Χs[rs_] := (rs^2+a^2)^2-a^2 Δs[rs];
κs[rs_] := a;
 
Σj[rt_, θt_] := rt^2+a^2 Cos[θt]^2;
Δj[rt_, θt_] := rt^2-2 rt+a^2+℧^2;
Χj[rt_, θt_] := (rt^2+a^2)^2-a^2 Sin[θt]^2 Δj[rt, θt];
ωj[rt_, θt_] := (a(2 rt-℧^2))/Χj[rt, θt];
ωR1 = ωj[R1, π/2];
 
ς = Abs@Sqrt[Χ/Δ/Σ]; ςr[rs_] := Abs@Sqrt[Χs[rs]/Δs[rs]/Σs[rs]];
μ = If[Abs[N@v0]==1.0, 0, -1];
 
j[v_] := Sqrt[1-v^2];
Ы[rs_]  := Sqrt[Χs[rs]/Σs[rs]];
ωs[rs_] := (a (2 rs - ℧^2))/Χs[rs];
 
ε[rs_, vt]  := Sqrt[Δs[rs] Σs[rs]/Χs[rs]]/j[vt]+Lz[rs, vt] ωs[rs];
Lz[rs_, vt] := vt Ы[rs]/j[vt];
 
nq[x_] := If[NumericQ[x], If[Element[x, Reals], x, 0], 0];
rl[x_] := If[Abs[Im[x]]>Abs[Re[x]], 1, x]

dΘF = Quiet[If[vL==0, 0, ArcCos[-vϑ/Sqrt[vr^2+vϑ^2+vφ^2]]]];
dθF = Quiet[If[vL==0, 0, If[vr>0, -dΘF, +dΘF]]];
dΦF = Quiet[If[vL==0, 0, ArcTan[Abs[vφ]/vr]]];
dφF = Quiet[If[vL==0, 0, If[vr!=0, -1, 1] If[vφ<0, +1, -1] If[NumericQ[dΦF], dΦF, π/2]]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 4) Geschwindigkeitskomponenten ||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
εj[rt_, δt_, δr_, δθ_, δφ_] := δt (1-(2 rt-℧^2)/rt^2)+(a δφ (2 rt-℧^2))/rt^2;
vrj[rt_, δt_, δr_, δθ_, δφ_] := δr/Sqrt[Δj[rt, θt]] Sqrt[Σj[rt, π/2]];
vθj[rt_, δt_, δr_, δθ_, δφ_] := δθ Sqrt[Σj[rt, π/2]];
vφj[rt_, δt_, δr_, δθ_, δφ_] := (-(((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+
rt^2) Sin[(π/2)] (-δφ-
(a q ℧ rt)/((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+rt^2))+
(εj[rt, δt, δr, δθ, δφ] Csc[(π/2)]^2 (a (-a^2-℧^2+2 rt-rt^2) Sin[(π/2)]^2+a (a^2+
rt^2) Sin[(π/2)]^2))/((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+rt^2))+(a q ℧ rt (a^2+
℧^2-2 rt+rt^2-a^2 Sin[(π/2)]^2))/((a^2 Cos[(π/2)]^2+rt^2)^2 (a^2+℧^2-2 rt+
rt^2))))/((a^2+℧^2-2 rt+rt^2-a^2 Sin[(π/2)]^2) Sqrt[((a^2+rt^2)^2-
a^2 (a^2+℧^2-2 rt+rt^2) Sin[(π/2)]^2)/(a^2 Cos[(π/2)]^2+rt^2)])));
 
vtj[rt_, δt_, δr_, δθ_, δφ_] := Sqrt[vrj[rt, δt, δr, δθ, δφ]^2+
vθj[rt, δt, δr, δθ, δφ]^2+vφj[rt, δt, δr, δθ, δφ]^2];
vφt[rt_, δt_, δr_, δθ_, δφ_] := vφj[rt, δt, δr, δθ, δφ]/vtj[rt, δt, δr, δθ, δφ];
shf[rt_, δt_, δr_, δθ_, δφ_] := Abs[ς/ςr[rt] Sqrt[1-vs[rt]^2]/(1-vs[rt] vφt[rt, δt, δr, δθ, δφ])];
 
dφv[rt_, tt_] := tt φs[rt]/ts[rt];
 
vθ  =-vϑ;
θs  = π/2;
θi  =-θ0+π;
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 5) Photonensphäre und ISCO ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
rp = ц/.Solve[4 a^2 (ц-℧^2)-(ц^2-3 ц+2 ℧^2)^2==0 && ц>=If[Element[rA, Reals], rA, 0], ц];
rP = 1.01 Min[rp]; Rp = 1.01 Max[rp];
isco = Quiet[Min[RI/.NSolve[0 == RI (6 RI-RI^2-9 ℧^2+3 a^2)+4 ℧^2 (℧^2-a^2)-8 a (RI-
℧^2)^(3/2) && RI>=If[Element[rA, Reals], rA, 0], RI]]];
{"r horizon" -> N@rA, "r ergosphere" -> N@rE, "r isco" -> N@isco,
"r photon pro" -> N@Min[rp], "r photon ret" -> N@Max[rp], "r disk" -> N@sr,
"r observer" -> N@r0, "θ observer" -> N@θ0 180/π}
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 6) Geschwindigkeit und Zeitdilatation auf der Scheibe |||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
red[rs_] := Quiet[Reduce[
dt == (Lz[rs, vt] (-a (a^2+rs^2)+Δs[rs] κs[rs])+ε[rs, vt] ((a^2+rs^2)^2-
Δs[rs] κs[rs]^2))/(Δs[rs] Σs[rs])
&&
0 == ((a^2+(-2+rs) rs+℧^2) (16 a dt dΦ rs (rs-℧^2)+8 dt^2 rs (-rs+℧^2)+
dΦ^2 rs (8 rs (-a^2+rs^3)+a^2 (4 a^2+4 ℧^2-4 (a-℧) (a+℧)))))/(8 rs^6)
&&
dΦ == (Lz[rs, vt] (-a^2+Δs[rs])+ε[rs, vt] (a (a^2+rs^2)-Δs[rs] κs[rs]))/(Δs[rs] Σs[rs])
&&
vt > 0,
{vt, dΦ, dt},
Reals]];
 
vs = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[1, 2]]],
red[rr][[1, 2]], 0]}, {rr, 0, sr, st}]];
φs = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[2, 2]]],
red[rr][[2, 2]], 0]}, {rr, 0, sr, st}]];
ts = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[3, 2]]],
red[rr][[3, 2]], 0]}, {rr, 0, sr, st}]];
 
"Akkretionsscheibe:"
 
plot[func_, label_] := Plot[func, {rr, si, sr},
GridLines -> {{nq[Min[rp]], nq[Max[rp]], nq[rA], nq[si], nq[isco], nq[rE], nq[sr]}, {}},
Frame -> True, ImagePadding -> {{40, 12}, {12, 12}}, ImageSize -> 340,
PlotLabel -> label, PlotRange->{{0, sr}, All}]
 
Grid[{{
plot[Sqrt[Χs[rr]/Δs[rr]/Σs[rr]],  "Gravitational time dilation: y=dt/dт, x=r"],
plot[φs[rr]/ts[rr], "Shapirodelayed angular velocity: y=dφ/dt, x=r"]},{
plot[ts[rr],  "Total time dilation: y=dt/dτ, x=r"],
plot[φs[rr],  "Coordinate speed: y=dφ/dτ, x=r"]}, {
plot[(a (2 rr-℧^2))/((a^2+rr^2)^2-a^2 (a^2-2 rr+rr^2+℧^2)), "Frame Dragging: y=dφ/dт, x=r"],
plot[vs[rr],  "Local velocity: y=v=dl/dτ, x=r"]}}]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 7) Frame Dragging und Gammafaktor |||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
й0 = (a (2 r0-℧^2) Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2-2 r0+r0^2+℧^2) Sin[θ0]^2)/((a^2-
2 r0+r0^2+℧^2) (r0^2+a^2 Cos[θ0]^2))])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2-
2 r0+r0^2+℧^2) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]);
vя = Sqrt[((a^2+r0^2)(℧^2-2r0))/(a^2 Sin[θ0]^2(a^2+(r0-2)r0+℧^2)-(a^2+r0^2)^2)];
vR = Sqrt[(2 r0-℧^2)/(a^2+r0^2)];
 
U = {+vr, +vθ, +vφ};
γ = 1/Sqrt[1-Norm[U]^2];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 8) Rotationsmatrix für die auf der Sichtebene eintreffenden Strahlen ||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
Xyz[{x_, y_, z_}, α_] := {x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z};
xYz[{x_, y_, z_}, β_] := {x Cos[β]+z Sin[β], y, z Cos[β]-x Sin[β]};
xyZ[{x_, y_, z_}, ψ_] := {x, y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]};
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 9) Raytracing Funktionscontainer ||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
raytracer[{Ф_, ϑ_}] :=
 
Quiet[Module[{DGL, sol, εj, pθi, pr0, Q, k, V, W, vw,
vr0i, vθ0i, vφ0i, vr0n, vθ0n, vφ0n, vr0a, vθia, vφ0a, vt0a,
t10, r10, Θ10, Φ10, t, r, θ, φ, τ,
т, т0, т1, т2, т3, т4, т5,
plunge, plunge0, plunge1, plunge2, plunge3,
plunge4, plunge5, plunge6, plunge7, plunge8,
dθ0, dφ0, δφ0, δθ0, δr0, δt0, tt0, rt0, θt0, φt0,
dθ1, dφ1, δφ1, δθ1, δr1, δt1, tt1, rt1, θt1, φt1,
dθ2, dφ2, δφ2, δθ2, δr2, δt2, tt2, rt2, θt2, φt2,
dθ3, dφ3, δφ3, δθ3, δr3, δt3, tt3, rt3, θt3, φt3,
dθ4, dφ4, δφ4, δθ4, δr4, δt4, tt4, rt4, θt4, φt4,
dθ5, dφ5, δφ5, δθ5, δr5, δt5, tt5, rt5, θt5, φt5,
dθ6, dφ6, δφ6, δθ6, δr6, δt6, tt6, rt6, θt6, φt6,
X, Y, Z, ξ, stepsize, laststep, mtl, ft, fτ, varb,
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0v, ft1v, ft2v, ft3v, ft4v, ft5v,
ft0f, ft1f, ft2f, ft3f, ft4f,
ft5h, ft5b, ft5f, ft5x, ft5y, fjet,
dt0y, dr0y, dθ0y, dφ0y,
initcon, shF,
rt8, θt8, φt8, δt8, δr8, δθ8, δφ8},
 
vw=xyZ[Xyz[{0, 1, 0}, ϑ], Ф+π/2];
                                 (* Übersetzung des Einfallswinkels in den lokalen Tetrad *)
vr0a = vw[[3]];
vφ0a = vw[[2]];
vθia = vw[[1]];
                                                                                (* Betrag *)
vt0a = Sqrt[vr0a^2+vφ0a^2+vθia^2];
                                                                            (* Normierung *)
vr0n = vr0a/vt0a;
vφ0n = vφ0a/vt0a;
vθ0n = vθia/vt0a;
                                              (* Relativistische Geschwindigkeitsaddition *)
V={vr0n, vθ0n, vφ0n};
W=(U+V+γ/(1+γ)(U\[Cross](U\[Cross]V)))/(1+U.V);
                                                                            (* Aberration *)
vr0i = W[[1]];
vθ0i = W[[2]];
vφ0i = W[[3]];

shF = Abs[If[vL==0, 1, Sqrt[1-vr^2-vϑ^2-vφ^2]/(1+vL (-Cos[If[vr>0, -dΘF, +dΘF]] Sin[ϑ]-
Sin[If[vr>0, -dΘF, +dΘF]] (Cos[-Ф-π/2+If[vr>0, -1, +1] ArcSin[vφ/vL]] Cos[ϑ] Cos[1/2 π]-
Cos[ϑ] Sin[-Ф-π/2+If[vr>0, -1, +1] ArcSin[vφ/vL]] Sin[1/2 π])))]];
 
initcon = TimeConstrained[NSolve[
dt0y == ς
&&
vr0i ==
Sqrt[(a^2 Cos[θi]^2+r0^2)/(a^2+℧^2-2 r0+r0^2)] Sqrt[1-μ^2 v0^2] dr0y
&&
vθ0i ==
Sqrt[a^2 Cos[θi]^2+r0^2] Sqrt[1-μ^2 v0^2] dθ0y
&&
vφ0i ==
(Sin[θi]^2 Sqrt[1-μ^2 v0^2] (a q μ^2 ℧ r0 v0^2+a (℧^2-
2 r0) dt0y+((a^2+r0^2)^2-a^2 (a^2+℧^2-
2 r0+r0^2) Sin[θi]^2) dφ0y))/((a^2 Cos[θi]^2+r0^2) Sqrt[(Sin[θi]^2 ((a^2+
r0^2)^2-a^2 (a^2+℧^2-2 r0+r0^2) Sin[θi]^2))/(a^2 Cos[θi]^2+r0^2)]),
{dt0y, dr0y, dθ0y, dφ0y}, Reals], 3];
                     
DGL = If[NumericQ[dt0y /. initcon[[1]]] == False, {}, {           (* Bewegungsgleichungen *)
 
t''[τ] == Re[-(1/((a^2 Cos[θ[τ]]^2+r[τ]^2)^2))((q ℧ (a^2 Cos[θ[τ]]^2-
r[τ]^2) (a^2+r[τ]^2) r'[τ])/(a^2+℧^2-2 r[τ]+r[τ]^2)-(2 (a^2 Cos[θ[τ]]^2+
℧^2 r[τ]-r[τ]^2) (a^2+r[τ]^2) r'[τ] t'[τ])/(a^2+℧^2-2 r[τ]+r[τ]^2)+
a^2 q ℧ r[τ] Sin[2 θ[τ]] θ'[τ]+a^2 (℧^2-2 r[τ]) Sin[2 θ[τ]] t'[τ] θ'[τ]+
(a (2 a^4 Cos[θ[τ]]^2+a^2 ℧^2 (3+Cos[2 θ[τ]]) r[τ]-a^2 (3+Cos[2 θ[τ]]) r[τ]^2+
4 ℧^2 r[τ]^3-6 r[τ]^4) Sin[θ[τ]]^2 r'[τ] φ'[τ])/(a^2+℧^2-2 r[τ]+r[τ]^2)-
2 a^3 Cos[θ[τ]] (℧^2-2 r[τ]) Sin[θ[τ]]^3 θ'[τ] φ'[τ])],
 
t'[0]  == dt0y/.initcon[[1]],
t[0]   == 0,
 
r''[τ] == Re[-(1/(2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^4))((2 (-a^2 Cos[θ[τ]]^2 (-1+r[τ])+(a^2+
℧^2-r[τ]) r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2)^3 r'[τ]^2)/(a^2+℧^2-2 r[τ]+r[τ]^2)+
q ℧ (a^2 Cos[θ[τ]]^2-r[τ]^2) (a^2+r[τ]^2) (a^2+2 ℧^2+a^2 Cos[2 θ[τ]]-4 r[τ]+
2 r[τ]^2) t'[τ]-2 a^2 q ℧ (℧^2-2 r[τ]) (a^2 Cos[θ[τ]]^2-r[τ]^2) Sin[θ[τ]]^2 t'[τ]-
2 (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2 Cos[θ[τ]]^2+r[τ]^2) (a^2+℧^2-2 r[τ]+
r[τ]^2) t'[τ]^2-4 a^2 Cos[θ[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2)^3 Sin[θ[τ]] r'[τ] θ'[τ]-
2 r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^3 (a^2+℧^2-2 r[τ]+r[τ]^2) θ'[τ]^2-2 a q ℧ (℧^2-
2 r[τ]) (a^2 Cos[θ[τ]]^2-r[τ]^2) (a^2+r[τ]^2) Sin[θ[τ]]^2 φ'[τ]+
2 a q ℧ (a^2 Cos[θ[τ]]^2-r[τ]^2) (-(a^2+r[τ]^2)^2 Sin[θ[τ]]^2+a^2 (a^2+
℧^2-2 r[τ]+r[τ]^2) Sin[θ[τ]]^4) φ'[τ]+4 a (a^2 Cos[θ[τ]]^2+(℧^2-
r[τ]) r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) (a^2+℧^2-2 r[τ]+r[τ]^2) Sin[θ[τ]]^2 t'[τ] φ'[τ]+
2 (a^2 Cos[θ[τ]]^2+r[τ]^2) (a^2+℧^2-2 r[τ]+r[τ]^2) Sin[θ[τ]]^2 (-r[τ] (-a^4+r[τ]^4+
a^2 (a^2+℧^2-r[τ]) Sin[θ[τ]]^2)+Cos[θ[τ]]^2 (-2 a^2 r[τ] (a^2+r[τ]^2)+a^4 (-1+
r[τ]) Sin[θ[τ]]^2)) φ'[τ]^2)],
 
r'[0]  == dr0y/.initcon[[1]],
r[0]   == r0,
 
θ''[τ] == Re[-(1/(2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3))((a^2 (a^2 Cos[θ[τ]]^2+
r[τ]^2)^2 Sin[2 θ[τ]] r'[τ]^2)/(a^2+℧^2-2 r[τ]+r[τ]^2)+4 r[τ] (a^2 Cos[θ[τ]]^2+
r[τ]^2)^2 r'[τ] θ'[τ]-1/8 Sin[2 θ[τ]] (8 r[τ]^6 φ'[τ]^2+16 a r[τ]^3 φ'[τ] (q ℧-
2 t'[τ]+2 a Sin[θ[τ]]^2 φ'[τ])+8 a^2 r[τ]^4 (θ'[τ]^2+(2+Cos[2 θ[τ]]) φ'[τ]^2)+
a^2 (-8 ℧^2 t'[τ]^2+8 a^4 Cos[θ[τ]]^4 θ'[τ]^2+16 a ℧^2 t'[τ] φ'[τ]+a^2 (3 a^2-
5 ℧^2+4 (a^2+℧^2) Cos[2 θ[τ]]+(a^2+℧^2) Cos[4 θ[τ]]) φ'[τ]^2)+
r[τ]^2 (16 a^4 Cos[θ[τ]]^2 θ'[τ]^2+a φ'[τ] (16 ℧^2 t'[τ]+a (11 a^2-
8 ℧^2+4 (3 a^2+2 ℧^2) Cos[2 θ[τ]]+a^2 Cos[4 θ[τ]]) φ'[τ]))+
8 a^2 r[τ] (2 t'[τ]^2-2 t'[τ] (q ℧+2 a φ'[τ])+a φ'[τ] (2 q ℧+
a (3+Cos[2 θ[τ]]) Sin[θ[τ]]^2 φ'[τ]))))],
 
θ'[0]  == dθ0y/.initcon[[1]],
θ[0]   == θi,
 
φ''[τ] == Re[-(1/(4 (a^2 Cos[θ[τ]]^2+r[τ]^2)^2))((4 a q ℧ (a^2 Cos[θ[τ]]^2-
r[τ]^2) r'[τ])/(a^2+℧^2-2 r[τ]+r[τ]^2)-(8 a (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-
r[τ]^2) r'[τ] t'[τ])/(a^2+℧^2-2 r[τ]+r[τ]^2)+8 a q ℧ Cot[θ[τ]] r[τ] θ'[τ]+
8 a Cot[θ[τ]] (℧^2-2 r[τ]) t'[τ] θ'[τ]+(1/(a^2+℧^2-2 r[τ]+r[τ]^2))(a^2 (3 a^2+
8 ℧^2+4 a^2 Cos[2 θ[τ]]+a^2 Cos[4 θ[τ]]) r[τ]-4 a^2 (3+Cos[2 θ[τ]]) r[τ]^2+
8 (a^2+℧^2+a^2 Cos[2 θ[τ]]) r[τ]^3-16 r[τ]^4+8 r[τ]^5+
2 a^4 Sin[2 θ[τ]]^2) r'[τ] φ'[τ]+Cot[θ[τ]] (a^2 (3 a^2-4 ℧^2+4 (a^2+
℧^2) Cos[2 θ[τ]]+a^2 Cos[4 θ[τ]])+16 a^2 Cos[θ[τ]]^2 r[τ]^2+8 r[τ]^4+
16 a^2 r[τ] Sin[θ[τ]]^2) θ'[τ] φ'[τ])],
 
φ'[0]  == dφ0y/.initcon[[1]],
φ[0]   == φ0,
 
WhenEvent[Abs[r[τ]] == N[R0]||Abs[r[τ]]>R0 &&
NumericQ[plunge6] == False,
(plunge6=τ) &&
(tt6=t[τ]) && (rt6=r[τ]) && (θt6=θ[τ]) && (φt6=φ[τ]);
"StopIntegration"],
 
WhenEvent[Abs[r[τ]] == N[R1] &&
NumericQ[plunge5] == False,
(plunge5=τ) && (tt5=t[τ]) && (rt5=r[τ]) && (θt5=θ[τ]) && (φt5=φ[τ]);
If[r0>R1, "StopIntegration"]],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && τ < -0.05 &&
NumericQ[plunge0] == False,
(plunge0=τ) &&
(tt0=t[τ]) && (rt0=r[τ]) && (θt0=θ[τ]) && (φt0=φ[τ]) &&
(δt0=t'[τ]) && (δr0=r'[τ]) && (δθ0=θ'[τ]) && (δφ0=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]>0 && τ < -0.05 &&
NumericQ[plunge1] == False,
(plunge1=τ) &&
(tt1=t[τ]) && (rt1=r[τ]) && (θt1=θ[τ]) && (φt1=φ[τ]) &&
(δt1=t'[τ]) && (δr1=r'[τ]) && (δθ1=θ'[τ]) && (δφ1=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 &&
r[τ]>N[si] && r[τ]<N[sr] && Re[θ'[τ]]<0 && τ < -0.05 &&
NumericQ[plunge2] == False,
(plunge2=τ) &&
(tt2=t[τ]) && (rt2=r[τ]) && (θt2=θ[τ]) && (φt2=φ[τ]) &&
(δt2=t'[τ]) && (δr2=r'[τ]) && (δθ2=θ'[τ]) && (δφ2=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]>0 &&
τ < plunge1-0.05 &&
NumericQ[plunge3] == False && NumericQ[plunge1] == True,
(plunge3=τ) &&
(tt3=t[τ]) && (rt3=r[τ]) && (θt3=θ[τ]) && (φt3=φ[τ]) &&
(δt3=t'[τ]) && (δr3=r'[τ]) && (δθ3=θ'[τ]) && (δφ3=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]<0 &&
τ < plunge2-0.05 &&
NumericQ[plunge4] == False && NumericQ[plunge2] == True,
(plunge4=τ) &&
(tt4=t[τ]) && (rt4=r[τ]) && (θt4=θ[τ]) && (φt4=φ[τ]) &&
(δt4=t'[τ]) && (δr4=r'[τ]) && (δθ4=θ'[τ]) && (δφ4=φ'[τ])],

WhenEvent[Mod[Re[θ[τ]], π] < θj/2 || Mod[Re[θ[τ]], π] > π-θj/2 &&
τ < -0.05 && NumericQ[plunge8] == False,
(plunge8=τ) &&
(tt8=t[τ]) && (rt8=r[τ]) && (θt8=θ[τ]) && (φt8=φ[τ]) &&
(δt8=t'[τ]) && (δr8=r'[τ]) && (δθ8=θ'[τ]) && (δφ8=φ'[τ])]
 
}];
                                                                            (* Integrator *)
sol = TimeConstrained[If[NumericQ[dt0y /. initcon[[1]]] == False, {},
NDSolve[DGL, {t, r, θ, φ}, {τ, 0, tmax},
WorkingPrecision-> wp,
Method-> mta,
MaxSteps-> Infinity,
StepMonitor :> (laststep=plunge7; plunge7=τ;
stepsize=plunge7-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-4, 0, 1])}
]], 10];
 
ft5h=If[NumericQ[plunge5], {φt5-π, θt5+π/2}, {0, -π/2}];
ft5b=If[NumericQ[plunge6], If[rt6<If[Element[rA, Reals], rA, 0], {0, -π/2},
If[rt6>4 R0, {0, -π/2}, {φt6-π, θt6+π/2}]], {0, -π/2}];
ft5f={0, Min[fmax, ς shF]};
ft5x=If[NumericQ[plunge6], {0, 1}, {0, 0}];
ft5y=If[NumericQ[plunge5], {0, 1}, {0, 0}];
 
ft0s=If[NumericQ[plunge0], {φt0, rt0}, {π, sr}];
ft1s=If[NumericQ[plunge1], {φt1, rt1}, {π, sr}];
ft2s=If[NumericQ[plunge2], {φt2, rt2}, {π, sr}];
ft3s=If[NumericQ[plunge3], {φt3, rt3}, {π, sr}];
ft4s=If[NumericQ[plunge4], {φt4, rt4}, {π, sr}];
 
ft0v=If[NumericQ[plunge0], {-dφv[rt0, tt0+t0+rT], 0}, {0, 0}];
ft1v=If[NumericQ[plunge1], {-dφv[rt1, tt1+t0+rT], 0}, {0, 0}];
ft2v=If[NumericQ[plunge2], {-dφv[rt2, tt2+t0+rT], 0}, {0, 0}];
ft3v=If[NumericQ[plunge3], {-dφv[rt3, tt3+t0+rT], 0}, {0, 0}];
ft4v=If[NumericQ[plunge4], {-dφv[rt4, tt4+t0+rT], 0}, {0, 0}];
ft5v=If[NumericQ[plunge5], {-(tt5+t0+rT) ωR1, 0}, {0, 0}];
 
ft0f=If[NumericQ[plunge0], {0, Min[fmax, shF shf[rt0, δt0, δr0, δθ0, δφ0]]}, {0, 0}];
ft1f=If[NumericQ[plunge1], {0, Min[fmax, shF shf[rt1, δt1, δr1, δθ1, δφ1]]}, {0, 0}];
ft2f=If[NumericQ[plunge2], {0, Min[fmax, shF shf[rt2, δt2, δr2, δθ2, δφ2]]}, {0, 0}];
ft3f=If[NumericQ[plunge3], {0, Min[fmax, shF shf[rt3, δt3, δr3, δθ3, δφ3]]}, {0, 0}];
ft4f=If[NumericQ[plunge4], {0, Min[fmax, shF shf[rt4, δt4, δr4, δθ4, δφ4]]}, {0, 0}];
fjet=If[NumericQ[plunge8], {0, 1}, {0, 0}];
{
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0s+ft0v, ft1s+ft1v, ft2s+ft2v, ft3s+ft3v, ft4s+ft4v,
ft0f, ft1f, ft2f, ft3f, ft4f,
ft5h+ft5v, ft5b, ft5f, ft5x, ft5y,
fjet, Fjet
}]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 10) Memoryfunktion ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
mem : raytrace[{Ф_, ϑ_}] := mem = Quiet[Re[raytracer[{Ф, ϑ}]]];
 
ray01[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[01]];
ray02[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[02]];
ray03[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[03]];
ray04[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[04]];
ray05[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[05]];
 
ray06[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[06]];
ray07[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[07]];
ray08[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[08]];
ray09[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[09]];
ray10[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[10]];
 
ray11[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[11]];
ray12[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[12]];
ray13[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[13]];
ray14[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[14]];
ray15[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[15]];
 
ray16[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[16]];
ray17[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[17]];
ray18[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[18]];
ray19[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[19]];
ray20[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[20]];
ray21[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[21]];
ray22[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[22]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 11) Proportionen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
width1  = ImageDimensions[pic1][[1]]; height1 = ImageDimensions[pic1][[2]];
width2  = ImageDimensions[pic2][[1]]; height2 = ImageDimensions[pic2][[2]];
width3  = ImageDimensions[pic3][[1]]; height3 = ImageDimensions[pic3][[2]];
width4  = ImageDimensions[pic4][[1]]; height4 = ImageDimensions[pic4][[2]];
width5  = ImageDimensions[pic5][[1]]; height5 = ImageDimensions[pic5][[2]];
width6  = ImageDimensions[pic7][[1]]; height6 = ImageDimensions[pic7][[2]];
hzoom   = If[breite>2 hoehe, 1/zoom, 1/zoom/2/hoehe*breite];
vzoom   = If[breite>2 hoehe, 1/zoom*2 hoehe/breite, 1/zoom];
 
"Geschätzte Rechenzeit" -> 1.2 (AbsoluteTiming[Do[raytracer[{
RandomReal[{-π, π}]/zoom, RandomReal[{-π/2, π/2}]/zoom
}], {ü, 1, 50}]][[1]])/50*hoehe*breite/kernels/60 "Minuten"
 
FOV->{360.0 hzoom "degree", 180.0 vzoom "degree"}
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 12) Output ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
img = ParallelTable[{
 
(* 1 Hintergrundpanorama *)
Quiet@ImageTransformation[pct1, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width1},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 2 Sphäre *)
Quiet@ImageTransformation[pct2, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-3π/2, π/2-2π/width2},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 3 Scheibe Textur komplett *)
Quiet@ImageTransformation[pic3, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 4 Scheibe Textur Front *)
Quiet@ImageTransformation[pic3, ray02, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 5 Scheibe Textur Echo 1 *)
Quiet@ImageTransformation[pic3, ray03, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 6 Scheibe Textur Echo 2 *)
Quiet@ImageTransformation[pic3, ray04, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 7 Scheibe Textur Echo 3 *)
Quiet@ImageTransformation[pic3, ray05, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 8 Scheibe Geometrie still komplett *)
Quiet@ImageTransformation[pic4, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 9 Scheibe Geometrie still Front *)
Quiet@ImageTransformation[pic4, ray02, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 10 Scheibe Geometrie still Echo 1 *)
Quiet@ImageTransformation[pic4, ray03, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 11 Scheibe Geometrie still Echo 2 *)
Quiet@ImageTransformation[pic4, ray04, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 12 Scheibe Geometrie still Echo 3 *)
Quiet@ImageTransformation[pic4, ray05, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 13 Scheibe Geometrie rotierend komplett *)
Quiet@ImageTransformation[pic4, ray06, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 14 Scheibe Geometrie rotierend Front *)
Quiet@ImageTransformation[pic4, ray07, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 15 Scheibe Geometrie rotierend Echo 1 *)
Quiet@ImageTransformation[pic4, ray08, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 16 Scheibe Geometrie rotierend Echo 2 *)
Quiet@ImageTransformation[pic4, ray09, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 17 Scheibe Geometrie rotierend Echo 3 *)
Quiet@ImageTransformation[pic4, ray10, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 18 Frequenzverschiebung komplett SW *)
Quiet@ImageTransformation[pic5, ray11, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-1, 1},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 19 Frequenzverschiebung Front SW *)
Quiet@ImageTransformation[pic5, ray12, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 20 Frequenzverschiebung Echo 1 SW *)
Quiet@ImageTransformation[pic5, ray13, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 21 Frequenzverschiebung Echo 2 SW *)
Quiet@ImageTransformation[pic5, ray14, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 22 Frequenzverschiebung Echo 3 SW *)
Quiet@ImageTransformation[pic5, ray15, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 23 Frequenzverschiebung komplett Farbe *)
Quiet@ImageTransformation[pic6, ray11, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 24 Frequenzverschiebung Front Farbe *)
Quiet@ImageTransformation[pic6, ray12, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 25 Frequenzverschiebung Echo 1 Farbe *)
Quiet@ImageTransformation[pic6, ray13, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 26 Frequenzverschiebung Echo 2 Farbe *)
Quiet@ImageTransformation[pic6, ray14, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 27 Frequenzverschiebung Echo 3 Farbe *)
Quiet@ImageTransformation[pic6, ray15, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 28 Hintergrundpanorama *)
ImageTransformation[pct3, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width6},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 29 Sphäre *)
ImageTransformation[pct3, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width6},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 30 Scheibe Textur komplett *)
ImageTransformation[pic7, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width6},
{si, sr+(sr-si)/height6}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 31 Frequenzverschiebung Hintergrund Farbe *)
Quiet@ImageTransformation[pic6, ray18, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 32 Frequenzverschiebung Hintergrund SW *)
Quiet@ImageTransformation[pic5, ray18, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 33 Kontur BH *)
Quiet@ImageTransformation[pic5, ray19, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 34 Kontur IH *)
Quiet@ImageTransformation[pic5, ray20, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 35 Jet 1 *)
Quiet@ImageTransformation[pic5, ray21, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 36 Jet 2 *)
Quiet@ImageTransformation[pic5, ray21, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"]
 
}, {x, 0, π-π/kernels/grain, π/kernels/grain}];
 
image[num_] := ImageAssemble[Table[{img[[x, num]]}, {x, kernels grain, 1, -1}]];
fi[x_] := ColorNegate[x];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 13) Composite |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
ParallelTable[image[n], {n, 1, 35, 1}]
 
ds1 = image[8]
ds2 = ImageMultiply[fi@image[09], fi@image[10]];
ds3 = ImageMultiply[fi@image[11], fi@image[12]];
ds4 = fi@ImageMultiply[ds2, ds3]
 
ds5 = image[13]
ds6 = ImageMultiply[fi@image[14], fi@image[15]];
ds7 = ImageMultiply[fi@image[16], fi@image[17]];
ds8 = fi@ImageMultiply[ds6, ds7]

bf1 = image[31]
bf2 = image[32]
bf3 = image[33]
bf4 = image[34]
 
bl1 = image[23]
bl2 = ImageMultiply[fi@image[24], fi@image[25]];
bl3 = ImageMultiply[fi@image[26], fi@image[27]];
bl4 = fi@ImageMultiply[bl2, bl3]
 
gr1 = image[18]
gr2 = ImageMultiply[fi@image[19], fi@image[20]];
gr3 = ImageMultiply[fi@image[21], fi@image[22]];
gr4 = fi@ImageMultiply[gr2, gr3]
 
sea = ImageMultiply[image[04], image[19]];
seb = ImageMultiply[image[05], image[20]];
sec = ImageMultiply[image[06], image[21]];
sed = ImageMultiply[image[07], image[22]];
 
se1 = image[03]
se2 = ImageMultiply[fi@image[04], fi@image[05]];
se3 = ImageMultiply[fi@image[06], fi@image[07]];
se4 = fi@ImageMultiply[se2, se3]
se5 = ImageMultiply[fi@sea, fi@seb];
se6 = ImageMultiply[fi@sec, fi@sed];
se7 = fi@ImageMultiply[se5, se6]
se8 = fi@ImageMultiply[fi@se7, fi@se7]
se9 = fi@ImageMultiply[fi@se8, fi@se7]
 
bkg = image[1]
hrz = image[2]
 
cb1 = image[28]
cb2 = image[29]
cb3 = image[30]

jet = image[35]
 
Quit[]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 14) Alternative initcon dt/dτ falls Partikel statt Photonen verwendet werden ||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
(* initcon = NSolve[
-μ  == -(((r0^2+a^2 Cos[θ0]^2) dr0y^2)/(a^2-2 r0+r0^2+℧^2))+((a^2-2 r0+
r0^2+℧^2-a^2 Sin[θ0]^2) (dt0y)^2)/(r0^2+a^2 Cos[θ0]^2)+(-r0^2-
a^2 Cos[θ0]^2) dθ0y^2+(2 a (2 r0-℧^2) Sin[θ0]^2 dt0y dφ0y)/(r0^2+
a^2 Cos[θ0]^2)+((-(a^2+r0^2)^2 Sin[θ0]^2+a^2 (a^2-2 r0+r0^2+
℧^2) Sin[θ0]^4) dφ0y^2)/(r0^2+a^2 Cos[θ0]^2)
&&
dt0y > 0
&&
vr0i ==
Sqrt[(a^2 Cos[θi]^2+r0^2)/(a^2+℧^2-2 r0+r0^2)] Sqrt[1-μ^2 v0^2] dr0y
&&
vθ0i ==
Sqrt[a^2 Cos[θi]^2+r0^2] Sqrt[1-μ^2 v0^2] dθ0y
&&
vφ0i ==
(Sin[θi]^2 Sqrt[1-μ^2 v0^2] (a q μ^2 ℧ r0 v0^2+a (℧^2-
2 r0) dt0y+((a^2+r0^2)^2-a^2 (a^2+℧^2-
2 r0+r0^2) Sin[θi]^2) dφ0y))/((a^2 Cos[θi]^2+r0^2) Sqrt[(Sin[θi]^2 ((a^2+
r0^2)^2-a^2 (a^2+℧^2-2 r0+r0^2) Sin[θi]^2))/(a^2 Cos[θi]^2+r0^2)]),
{dt0y, dr0y, dθ0y, dφ0y}, Reals];                                                         *)










Wenn der Beobachter nahe oder hinter dem Horizont ist empfehlen sich Raindrop Doran Koordinaten (Beispiel: klick, Animation: .nb-File):

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* > raytracing.yukterez.net | 07.04.2018 - 09.09.2020 | Version 20 | Simon Tyran, Vienna *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
Pause[1]                                                    (* Raindrop Doran Koordinaten *)
 
wp  = MachinePrecision;
mt0 = Automatic;
mt1 = {"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mta = mt0;                                (* mt0 für Geschwindigkeit, mt1 für Genauigkeit *)
 
kernels = 6;                                                          (* Parallelisierung *)
grain   = 5;                            (* Subparallelisierung auf kernels*grain Streifen *)
rsp     = "Nearest";                                                        (* Resampling *)
 
breite  = 240;                                               (* Zielabmessungen in Pixeln *)
hoehe   = 120;          (* Höhe sollte ein ganzzahliges Vielfaches von kernels*grain sein *)
zoom    = 1;                                  (* doppelter Zoom ergibt halben Sichtwinkel *)
 
LaunchKernels[kernels]
wp = MachinePrecision;                                                     (* Genauigkeit *)
st = 0.01;                                                    (* Auflösung des Gradienten *)
 
pic1 = Import["http://www.yukterez.net/mw/1/flip70.png"];    (* Hintergrundpanorama laden *)
pic2 = Import["http://www.yukterez.net/mw/1/worldmap.png"];    (* Sphärenoberfläche laden *)
pic3 = Import["http://www.yukterez.net/mw/akkretionsscheibe.jpg"];(* Scheibentextur laden *)
pic4 = Import["http://www.yukterez.net/mw/disk.png"];          (* Scheibengeometrie laden *)
pic5 = Import["http://www.yukterez.net/mw/gradient1.png"];   (* Helligkeitsgradient laden *)
pic6 = Import["http://www.yukterez.net/mw/gradient2.png"];          (* Farbgradient laden *)
pic7 = Import["http://www.yukterez.net/mw/1/cl.png"];               (* Checkerboard laden *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 1) Startbedingungen und Position des Beobachters ||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0 = 10;                                              (* Radialkoordinate des Beobachters *)
R0 = 500;                                (* Radius des umspannenden Kugelschalenpanoramas *)
R1 = Max[1, Re[1.0001 rA]];                                                     (* Sphäre *)
rT = 10;                                                 (* Lichtlaufzeit Synchronisation *)
t0 = 0;                                                      (* Eigenzeit des Beobachters *)

si = isco+0.1;                                           (* Akkretionsscheibe Innenradius *)
sr = 7;                                                  (* Akkretionsscheibe Außenradius *)

θ0 = 70 π/180;                                                             (* Breitengrad *)
φ0 = 0;                                                                     (* Längengrad *)
 
tmax = -100 R0;                                         (* zeitlicher Integrationsbereich *)
 
a  = 0.7;                                                                (* Spinparameter *)
℧  = 0.7;                                       (* spezifische Ladung des schwarzen Lochs *)
v0 = 1;                                                   (* Geschwindigkeit der Photonen *)
 
vr = 0;                                   (* Radiale Geschwindigkeit relativ zum Raindrop *)
vϑ = 0;                                         (* Polare Geschwindigkeit des Beobachters *)
vφ = 0;       (* Azimutale Geschwindigkeit des Beobachters: 0 für ZAMO, -й0 für stationär *)

vL = Sqrt[vr^2+vϑ^2+vφ^2];
 
hvs  = 0; (* ArcSin[vφ/vL] *)                        (* horizontaler Versatz in Radianten *)
vvs  = 0; (* ArcSin[vϑ/vL] *)                          (* vertikaler Versatz in Radianten *)

fmax = 2; fmin = 0;                                            (* Doppler Frequenzbereich *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 2) Bildreflektion |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
fpt[{x_, y_}] := {If[y<0, x+1, x], If[y<0, -y, y]}
 
pcr1 = ParallelTable[
Quiet@ImageTransformation[pic1, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}},
Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct1 = ImageAssemble[Table[{pcr1[[x]]}, {x, 2 kernels, 1, -1}]];
 
pcr2 = ParallelTable[
Quiet@ImageTransformation[pic2, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}},
Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct2 = ImageAssemble[Table[{pcr2[[x]]}, {x, 2 kernels, 1, -1}]];
 
pcr3 = ParallelTable[
ImageTransformation[pic7, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct3 = ImageAssemble[Table[{pcr3[[x]]}, {x, 2 kernels, 1, -1}]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 3) Funktionen |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
g11 = gtt = 1+(-4 r0+2 ℧^2)/(a^2+2 r0^2+a^2 Cos[2 θ0]);
g22 = grr = -((a^2+2 r0^2+a^2 Cos[2 θ0])/(2 (a^2+r0^2)));
g33 = gθθ = -r0^2-a^2 Cos[θ0]^2;
g44 = gφφ = (-(a^2+r0^2)^2 Sin[θ0]^2+a^2 (a^2+(-2+r0) r0+℧^2) Sin[θ0]^4)/(r0^2+a^2 Cos[θ0]^2);
g12 = gtr = -(Sqrt[2 r0-℧^2]/Sqrt[a^2+r0^2]);
g14 = gtφ = (a (2 r0-℧^2) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2);
g24 = grφ = (a Sqrt[2 r0-℧^2] Sin[θ0]^2)/Sqrt[a^2+r0^2];
g13 = g23 = g34 = 0;

rA  = 1+Sqrt[1-a^2-℧^2];
rI  = 1-Sqrt[1-a^2-℧^2];
rE  = 1+Sqrt[1-℧^2-a^2 Cos[θ0]^2];
rG  = 1-Sqrt[1-℧^2-a^2 Cos[θ0]^2];
 
q = 0;
 
Σ = r0^2+a^2 Cos[θ0]^2;
Δ = r0^2-2 r0+a^2+℧^2;
Χ = (r0^2+a^2)^2-a^2 Sin[θ0]^2 Δ;
 
Σs[rs_] := rs^2;
Δs[rs_] := rs^2-2 rs+a^2+℧^2;
Χs[rs_] := (rs^2+a^2)^2-a^2 Δs[rs];
κs[rs_] := a;
 
Σj[rt_, θt_] := rt^2+a^2 Cos[θt]^2;
Δj[rt_, θt_] := rt^2-2 rt+a^2+℧^2;
Χj[rt_, θt_] := (rt^2+a^2)^2-a^2 Sin[θt]^2 Δj[rt, θt];
ωj[rt_, θt_] := (a(2 rt-℧^2))/Χj[rt, θt];
ωR1 = ωj[R1, π/2];
 
ς = Abs@Sqrt[Χ/Δ/Σ]; ςr[rs_] := Abs@Sqrt[Χs[rs]/Δs[rs]/Σs[rs]];
μ = If[Abs[N@v0]==1.0, 0, -1];
 
j[v_] := Sqrt[1-v^2];
Ы[rs_]  := Sqrt[Χs[rs]/Σs[rs]];
ωs[rs_] := (a (2 rs - ℧^2))/Χs[rs];
 
ε[rs_, vt_]  := Sqrt[Δs[rs] Σs[rs]/Χs[rs]]/j[vt]+Lz[rs, vt] ωs[rs];
Lz[rs_, vt_] := vt Ы[rs]/j[vt];
 
nq[x_] := If[NumericQ[x], If[Element[x, Reals], x, 0], 0];

dΘF = Quiet[If[vLF==0, 0, ArcCos[-vθF/Sqrt[vrF^2+vθF^2+vφF^2]]]];
dθF = Quiet[If[vLF==0, 0, If[vrF>0, -dΘF, +dΘF]]];
dΦF = Quiet[If[vLF==0, 0, ArcTan[Abs[vφF]/vrF]]];
dφF = Quiet[If[vLF==0, 0, If[vrF!=0, -1, 1] If[vφF<0, +1, -1] If[NumericQ[dΦF], dΦF, π/2]]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 4) Geschwindigkeitskomponenten ||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
εj[rt_, δt_, δr_, δθ_, δφ_] := (δt-δr Sqrt[(2rt-℧^2)/(a^2+rt^2)]/(1-(2rt-℧^2)/(a^2+
rt^2))) (1-(2 rt-℧^2)/rt^2)+(a (δφ-δr a Sqrt[(2rt-℧^2)/(a^2+rt^2)]/(1-(2rt-℧^2)/(a^2+
rt^2))/(a^2+rt^2)) (2 rt-℧^2))/rt^2;

vrj[rt_, δt_, δr_, δθ_, δφ_] := δr/Sqrt[Δj[rt, θt]] Sqrt[Σj[rt, π/2]];
vθj[rt_, δt_, δr_, δθ_, δφ_] := δθ Sqrt[Σj[rt, π/2]];
vφj[rt_, δt_, δr_, δθ_, δφ_] := (-(((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+
rt^2) Sin[(π/2)] (-(δφ-δr a Sqrt[(2rt-℧^2)/(a^2+rt^2)]/(1-(2rt-℧^2)/(a^2+rt^2))/(a^2+rt^2))-
(a q ℧ rt)/((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+rt^2))+
(εj[rt, δt, δr, δθ, δφ] Csc[(π/2)]^2 (a (-a^2-℧^2+2 rt-rt^2) Sin[(π/2)]^2+a (a^2+
rt^2) Sin[(π/2)]^2))/((a^2 Cos[(π/2)]^2+rt^2) (a^2+℧^2-2 rt+rt^2))+(a q ℧ rt (a^2+
℧^2-2 rt+rt^2-a^2 Sin[(π/2)]^2))/((a^2 Cos[(π/2)]^2+rt^2)^2 (a^2+℧^2-2 rt+
rt^2))))/((a^2+℧^2-2 rt+rt^2-a^2 Sin[(π/2)]^2) Sqrt[((a^2+rt^2)^2-
a^2 (a^2+℧^2-2 rt+rt^2) Sin[(π/2)]^2)/(a^2 Cos[(π/2)]^2+rt^2)])));

vtj[rt_, δt_, δr_, δθ_, δφ_] := Sqrt[vrj[rt, δt, δr, δθ, δφ]^2+
vθj[rt, δt, δr, δθ, δφ]^2+vφj[rt, δt, δr, δθ, δφ]^2];
vφt[rt_, δt_, δr_, δθ_, δφ_] := vφj[rt, δt, δr, δθ, δφ]/vtj[rt, δt, δr, δθ, δφ];
shf[rt_, δt_, δr_, δθ_, δφ_] := Abs[ς/ςr[rt] Sqrt[1-vs[rt]^2]/(1-vs[rt] vφt[rt, δt, δr, δθ, δφ])];

dφv[rt_, tt_] := tt φs[rt]/ts[rt];

vsolve = Block[{r=r0, θ=θ0, μ=-1, q=0},

ini = NSolve[
vr ==
(Sqrt[2] Sqrt[1-μ^2 vL^2] ((q μ^2 ℧ r Sqrt[-℧^2+2 r] vL^2)/((a^2+℧^2+
(-2+r) r) Sqrt[a^2+r^2])+((a^2+a^2 Cos[2 θ]+2 r^2) dR)/(2 (a^2+r^2))+(Sqrt[-℧^2+2 r] (dT-
a Sin[θ]^2 dΦ))/Sqrt[a^2+r^2]))/Sqrt[(a^2+a^2 Cos[2 θ]+2 r^2)/(a^2+r^2)]
&&
vϑ ==
Sqrt[a^2 Cos[θ]^2+r^2] Sqrt[1-μ^2 vL^2] dΘ
&&
vφ ==
(Sin[θ]^2 Sqrt[1-μ^2 vL^2] (a q μ^2 ℧ r Sqrt[a^2+r^2] vL^2-1/2 a Sqrt[-℧^2+2 r] (a^2+
a^2 Cos[2 θ]+2 r^2) dR+Sqrt[a^2+r^2] (a (℧^2-2 r) dT+((a^2+r^2)^2-a^2 (a^2+℧^2-2 r+
r^2) Sin[θ]^2) dΦ)))/(Sqrt[a^2+r^2] (a^2 Cos[θ]^2+r^2) Sqrt[(Sin[θ]^2 ((a^2+r^2)^2-
a^2 (a^2+℧^2-2 r+r^2) Sin[θ]^2))/(a^2 Cos[θ]^2+r^2)])
&&
-μ ==
-(((a^2+2 r^2+
a^2 Cos[2 θ]) (dR)^2)/(2 (a^2+r^2)))-(2 Sqrt[2 r-℧^2] dR dT)/Sqrt[a^2+r^2]+(1+(-4 r+
2 ℧^2)/(a^2+2 r^2+a^2 Cos[2 θ])) (dT)^2+(-r^2-a^2 Cos[θ]^2) dΘ^2+(2 a Sqrt[2 r-
℧^2] Sin[θ]^2 dR dΦ)/Sqrt[a^2+r^2]+(2 a (2 r-℧^2) Sin[θ]^2 dT dΦ)/(r^2+a^2 Cos[θ]^2)+
((-(a^2+r^2)^2 Sin[θ]^2+a^2 (a^2+(-2+r) r+℧^2) Sin[θ]^4) (dΦ)^2)/(r^2+a^2 Cos[θ]^2)
&&
dT > 0,
{dT, dR, dΘ, dΦ},
Reals];

β = -Sqrt[(2r-℧^2)/(a^2+r^2)];

drf = (dR/.ini[[1]]);
dθf = (dΘ/.ini[[1]]);
dΔf = drf a β/(1-β^2)/(a^2+r^2);
dφf = (dΦ/.ini[[1]])-dΔf;
dφF = (dΦ/.ini[[1]])+dΔf;

{
NSolve[
vrf ==
Sqrt[(a^2 Cos[θ]^2+r^2)/(a^2+℧^2-2 r+r^2)] Sqrt[1-μ^2 v0f^2] drf
&&
vϑf == Sqrt[a^2 Cos[θ]^2+r^2] Sqrt[1-μ^2 v0f^2] dθf
&&
vφf == (Sin[θ]^2 Sqrt[1-μ^2 v0f^2] (a q μ^2 ℧ r v0f^2+a (℧^2-2 r) dtf+((a^2+r^2)^2-
a^2 (a^2+℧^2-2 r+r^2) Sin[θ]^2) dφf))/((a^2 Cos[θ]^2+r^2) Sqrt[(Sin[θ]^2 ((a^2+
r^2)^2-a^2 (a^2+℧^2-2 r+r^2) Sin[θ]^2))/(a^2 Cos[θ]^2+r^2)])
&&
v0f == Sqrt[vrf^2+vϑf^2+vφf^2]
&&
-μ == -(((r^2+a^2 Cos[θ]^2) drf^2)/(a^2-2 r+r^2+℧^2))+((a^2-2 r+r^2+℧^2-
a^2 Sin[θ]^2) (dtf)^2)/(r^2+a^2 Cos[θ]^2)+(-r^2-a^2 Cos[θ]^2) dθf^2+(2 a (2 r-
℧^2) Sin[θ]^2 dtf dφf)/(r^2+a^2 Cos[θ]^2)+((-(a^2+r^2)^2 Sin[θ]^2+a^2 (a^2-2 r+
r^2+℧^2) Sin[θ]^4) dφf^2)/(r^2+a^2 Cos[θ]^2)
&&
dtf>0,
{dtf, vrf, vϑf, vφf, v0f}],

NSolve[
vrf ==
Sqrt[(a^2 Cos[θ]^2+r^2)/(a^2+℧^2-2 r+r^2)] Sqrt[1-μ^2 v0f^2] drf
&&
vϑf == Sqrt[a^2 Cos[θ]^2+r^2] Sqrt[1-μ^2 v0f^2] dθf
&&
vφf == (Sin[θ]^2 Sqrt[1-μ^2 v0f^2] (a q μ^2 ℧ r v0f^2+a (℧^2-2 r) dtf+((a^2+r^2)^2-
a^2 (a^2+℧^2-2 r+r^2) Sin[θ]^2) dφF))/((a^2 Cos[θ]^2+r^2) Sqrt[(Sin[θ]^2 ((a^2+
r^2)^2-a^2 (a^2+℧^2-2 r+r^2) Sin[θ]^2))/(a^2 Cos[θ]^2+r^2)])
&&
v0f == Sqrt[vrf^2+vϑf^2+vφf^2]
&&
-μ == -(((r^2+a^2 Cos[θ]^2) drf^2)/(a^2-2 r+r^2+℧^2))+((a^2-2 r+r^2+℧^2-
a^2 Sin[θ]^2) (dtf)^2)/(r^2+a^2 Cos[θ]^2)+(-r^2-a^2 Cos[θ]^2) dθf^2+(2 a (2 r-
℧^2) Sin[θ]^2 dtf dφF)/(r^2+a^2 Cos[θ]^2)+((-(a^2+r^2)^2 Sin[θ]^2+a^2 (a^2-2 r+
r^2+℧^2) Sin[θ]^4) dφF^2)/(r^2+a^2 Cos[θ]^2)
&&
dtf>0,
{dtf, vrf, vϑf, vφf, v0f}]
}];

vrFx = Quiet[vrf/.vsolve[[1]]][[1]];
vθFx = Quiet[vϑf/.vsolve[[1]]][[1]];
vφFx = Quiet[vφf/.vsolve[[1]]][[1]];

VrFx = Quiet[vrf/.vsolve[[2]]][[1]];
VθFx = Quiet[vϑf/.vsolve[[2]]][[1]];
VφFx = Quiet[vφf/.vsolve[[2]]][[1]];

vθF = Quiet[Re[vθFx]+Im[vθFx]];
vφF = Quiet[Re[vφFx]+Im[vφFx]];
vLF = Quiet[Sqrt[vrFx^2+vθF^2+vφF^2]];
vrF = Quiet[If[vLF<1,vrFx,-vrFx]];

VθF = Quiet[Re[VθFx]+Im[VθFx]];
VφF = Quiet[Re[VφFx]+Im[VφFx]];
VLF = Quiet[Sqrt[VrFx^2+VθF^2+VφF^2]];
VrF = Quiet[If[VLF<1,VrFx,-VrFx]];

vθ  =-vϑ;
θs  = π/2;
θi  =-θ0+π;
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 5) Photonensphäre und ISCO ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
rp = ц/.Solve[4 a^2 (ц-℧^2)-(ц^2-3 ц+2 ℧^2)^2==0 && ц>=If[Element[rA, Reals], rA, 0], ц];
rP = 1.01 Min[rp]; Rp = 1.01 Max[rp];
isco = Quiet[Min[RI/.NSolve[0 == RI (6 RI-RI^2-9 ℧^2+3 a^2)+4 ℧^2 (℧^2-a^2)-8 a (RI-
℧^2)^(3/2) && RI>=If[Element[rA, Reals], rA, 0], RI]]];
{"r horizon" -> N@rA, "r ergosphere" -> N@rE, "r isco" -> N@isco,
"r photon pro" -> N@Min[rp], "r photon ret" -> N@Max[rp], "r disk" -> N@sr,
"r observer" -> N@r0, "θ observer" -> N@θ0 180/π}
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 6) Geschwindigkeit und Zeitdilatation auf der Scheibe |||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
red[rs_] := Quiet[Reduce[
dt == (Lz[rs, vt] (-a (a^2+rs^2)+Δs[rs] κs[rs])+ε[rs, vt] ((a^2+rs^2)^2-
Δs[rs] κs[rs]^2))/(Δs[rs] Σs[rs])
&&
0 == ((a^2+(-2+rs) rs+℧^2) (16 a dt dΦ rs (rs-℧^2)+8 dt^2 rs (-rs+℧^2)+
dΦ^2 rs (8 rs (-a^2+rs^3)+a^2 (4 a^2+4 ℧^2-4 (a-℧) (a+℧)))))/(8 rs^6)
&&
dΦ == (Lz[rs, vt] (-a^2+Δs[rs])+ε[rs, vt] (a (a^2+rs^2)-Δs[rs] κs[rs]))/(Δs[rs] Σs[rs])
&&
vt > 0,
{vt, dΦ, dt},
Reals]];
 
vs = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[1, 2]]],
red[rr][[1, 2]], 0]}, {rr, 0, sr, st}]];
φs = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[2, 2]]],
red[rr][[2, 2]], 0]}, {rr, 0, sr, st}]];
ts = Interpolation[ParallelTable[{rr, If[Quiet@NumericQ[red[rr][[3, 2]]],
red[rr][[3, 2]], 0]}, {rr, 0, sr, st}]];
 
"Akkretionsscheibe:"
 
plot[func_, label_] := Plot[func, {rr, si, sr},
GridLines -> {{nq[Min[rp]], nq[Max[rp]], nq[rA], nq[si], nq[isco], nq[rE], nq[sr]}, {}},
Frame -> True, ImagePadding -> {{40, 12}, {12, 12}}, ImageSize -> 340,
PlotLabel -> label, PlotRange->{{0, sr}, All}]
 
Grid[{{
plot[Sqrt[Χs[rr]/Δs[rr]/Σs[rr]],  "Gravitational time dilation: y=dt/dт, x=r"],
plot[φs[rr]/ts[rr], "Shapirodelayed angular velocity: y=dφ/dt, x=r"]},{
plot[ts[rr],  "Total time dilation: y=dt/dτ, x=r"],
plot[φs[rr],  "Coordinate speed: y=dφ/dτ, x=r"]}, {
plot[(a (2 rr-℧^2))/((a^2+rr^2)^2-a^2 (a^2-2 rr+rr^2+℧^2)), "Frame Dragging: y=dφ/dт, x=r"],
plot[vs[rr],  "Local velocity: y=v=dl/dτ, x=r"]}}]
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 7) Frame Dragging und Gammafaktor |||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
й0 = (a (2 r0-℧^2) Sin[θ0] Sqrt[((a^2+r0^2)^2-a^2 (a^2-2 r0+r0^2+℧^2) Sin[θ0]^2)/((a^2-
2 r0+r0^2+℧^2) (r0^2+a^2 Cos[θ0]^2))])/((r0^2+a^2 Cos[θ0]^2) Sqrt[((a^2+r0^2)^2-a^2 (a^2-
2 r0+r0^2+℧^2) Sin[θ0]^2)/(r0^2+a^2 Cos[θ0]^2)]);
vя = Sqrt[((a^2+r0^2)(℧^2-2r0))/(a^2 Sin[θ0]^2(a^2+(r0-2)r0+℧^2)-(a^2+r0^2)^2)];
vR = Sqrt[(2 r0-℧^2)/(a^2+r0^2)];
 
U = {+vr, +vθ, +vφ};
γ = 1/Sqrt[1-Norm[U]^2];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 8) Rotationsmatrix für die auf der Sichtebene eintreffenden Strahlen ||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
Xyz[{x_, y_, z_}, α_] := {x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z};
xYz[{x_, y_, z_}, β_] := {x Cos[β]+z Sin[β], y, z Cos[β]-x Sin[β]};
xyZ[{x_, y_, z_}, ψ_] := {x, y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]};
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 9) Raytracing Funktionscontainer ||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
raytracer[{Ф_, ϑ_}] :=
 
Quiet[Module[{DGL, sol, εj, pθi, pr0, Q, k, V, W, vw,
vr0i, vθ0i, vφ0i, vr0n, vθ0n, vφ0n, vr0a, vθia, vφ0a, vt0a,
t10, r10, Θ10, Φ10, t, r, θ, φ, τ,
т, т0, т1, т2, т3, т4, т5,
plunge, plunge0, plunge1, plunge2, plunge3,
plunge4, plunge5, plunge6, plunge7,
dθ0, dφ0, δφ0, δθ0, δr0, δt0, tt0, rt0, θt0, φt0,
dθ1, dφ1, δφ1, δθ1, δr1, δt1, tt1, rt1, θt1, φt1,
dθ2, dφ2, δφ2, δθ2, δr2, δt2, tt2, rt2, θt2, φt2,
dθ3, dφ3, δφ3, δθ3, δr3, δt3, tt3, rt3, θt3, φt3,
dθ4, dφ4, δφ4, δθ4, δr4, δt4, tt4, rt4, θt4, φt4,
dθ5, dφ5, δφ5, δθ5, δr5, δt5, tt5, rt5, θt5, φt5,
dθ6, dφ6, δφ6, δθ6, δr6, δt6, tt6, rt6, θt6, φt6,
X, Y, Z, ξ, stepsize, laststep, mtl, ft, fτ, varb,
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0v, ft1v, ft2v, ft3v, ft4v, ft5v,
ft0f, ft1f, ft2f, ft3f, ft4f, ft5f,
ft0F, ft1F, ft2F, ft3F, ft4F, ft5F,
ft5h, ft5b, ft5x, ft5y,
dt0y, dr0y, dθ0y, dφ0y,
initcon, shF, ShF},
 
vw=xyZ[Xyz[{0, 1, 0}, ϑ], Ф+π/2];
                                 (* Übersetzung des Einfallswinkels in den lokalen Tetrad *)
vr0a = vw[[3]];
vφ0a = vw[[2]];
vθia = vw[[1]];
                                                                                (* Betrag *)
vt0a = Sqrt[vr0a^2+vφ0a^2+vθia^2];
                                                                            (* Normierung *)
vr0n = vr0a/vt0a;
vφ0n = vφ0a/vt0a;
vθ0n = vθia/vt0a;
                                              (* Relativistische Geschwindigkeitsaddition *)
V={vr0n, vθ0n, vφ0n};
W=(U+V+γ/(1+γ)(U\[Cross](U\[Cross]V)))/(1+U.V);
                                                                            (* Aberration *)
vr0i = W[[1]];
vθ0i = W[[2]];
vφ0i = W[[3]];

shF = Abs[If[vLF==0, 1, Sqrt[1-vLF^2]/(1+vLF (-Cos[If[vrF>0, -dΘF, +dΘF]] Sin[ϑ]-
Sin[If[vrF>0, -dΘF, +dΘF]] (Cos[-Ф-π/2+If[vrF>0, -1,
1] ArcSin[vφF/vLF]] Cos[ϑ] Cos[1/2 π If[vφF<0,
1, -1] If[vrF!=0,-1,1]]-Cos[ϑ] Sin[-Ф-π/2+
If[vrF>0, -1, +1]ArcSin[vφF/vLF]] Sin[1/2 π])))]];

ShF = Abs[If[VLF==0, 1, Sqrt[1-VLF^2]/(1+VLF (-Cos[If[VrF>0, -dΘF, +dΘF]] Sin[ϑ]-
Sin[If[VrF>0, -dΘF, +dΘF]] (Cos[-Ф-π/2+If[VrF>0, -1,
1] ArcSin[VφF/VLF]] Cos[ϑ] Cos[1/2 π If[VφF<0,
1, -1] If[VrF!=0,-1,1]]-Cos[ϑ] Sin[-Ф-π/2+
If[VrF>0, -1, +1]ArcSin[VφF/VLF]] Sin[1/2 π])))]];
 
initcon = TimeConstrained[NSolve[
vr0i ==
N[(Sqrt[2] Sqrt[1-μ^2 v0^2] ((q μ^2 ℧ r0 Sqrt[-℧^2+2 r0] v0^2)/((a^2+℧^2+(-2+
r0) r0) Sqrt[a^2+r0^2])+((a^2+a^2 Cos[2 θi]+2 r0^2) dr0y)/(2 (a^2+r0^2))+(Sqrt[-℧^2+
2 r0] (dt0y-a Sin[θi]^2 dφ0y))/Sqrt[a^2+r0^2]))/Sqrt[(a^2+a^2 Cos[2 θi]+2 r0^2)/(a^2+r0^2)]]
&&
vθ0i ==
N[Sqrt[a^2 Cos[θi]^2+r0^2] Sqrt[1-μ^2 v0^2] dθ0y]
&&
vφ0i ==
N[(Sin[θi]^2 Sqrt[1-μ^2 v0^2] (a q μ^2 ℧ r0 Sqrt[a^2+r0^2] v0^2-1/2 a Sqrt[-℧^2+2 r0] (a^2+
a^2 Cos[2 θi]+2 r0^2) dr0y+Sqrt[a^2+r0^2] (a (℧^2-2 r0) dt0y+((a^2+r0^2)^2-a^2 (a^2+℧^2-
2 r0+r0^2) Sin[θi]^2) dφ0y)))/(Sqrt[a^2+r0^2] (a^2 Cos[θi]^2+r0^2) Sqrt[(Sin[θi]^2 ((a^2+
r0^2)^2-a^2 (a^2+℧^2-2 r0+r0^2) Sin[θi]^2))/(a^2 Cos[θi]^2+r0^2)])]
&&
-μ ==
N[-(((a^2+2 r0^2+a^2 Cos[2 θi]) (dr0y)^2)/(2 (a^2+r0^2)))-(2 Sqrt[2 r0-
℧^2] dr0y dt0y)/Sqrt[a^2+r0^2]+(1+(-4 r0+2 ℧^2)/(a^2+2 r0^2+a^2 Cos[2 θi])) (dt0y)^2+
(-r0^2-a^2 Cos[θi]^2) dθ0y^2+(2 a Sqrt[2 r0-℧^2] Sin[θi]^2 dr0y dφ0y)/Sqrt[a^2+
r0^2]+(2 a (2 r0-℧^2) Sin[θi]^2 dt0y dφ0y)/(r0^2+a^2 Cos[θi]^2)+((-(a^2+r0^2)^2 Sin[θi]^2+
a^2 (a^2+(-2+r0) r0+℧^2) Sin[θi]^4) (dφ0y)^2)/(r0^2+a^2 Cos[θi]^2)]
&&
dt0y > 0,
{dθ0y, dr0y, dt0y, dφ0y}, Reals], 3];
                     
DGL = If[NumericQ[dt0y /. initcon[[1]]] == False, {}, {           (* Bewegungsgleichungen *)
 
t''[τ] == Re[1/(8 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3) (8 q ℧ (-a^4 Cos[θ[τ]]^4+r[τ]^4) r'[τ]+
(8 (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 r'[τ]^2)/(Sqrt[-℧^2+
2 r[τ]] Sqrt[a^2+r[τ]^2])+8 q ℧ Sqrt[-℧^2+2 r[τ]] Sqrt[a^2+r[τ]^2] (-a^2 Cos[θ[τ]]^2+
r[τ]^2) t'[τ]+16 (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2 Cos[θ[τ]]^2+r[τ]^2) r'[τ] t'[τ]+
8 Sqrt[-℧^2+2 r[τ]] (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) Sqrt[a^2+r[τ]^2] t'[τ]^2-
8 a^2 q ℧ r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[2 θ[τ]] θ'[τ]+(8 a^2 Sqrt[-℧^2+
2 r[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 Sin[2 θ[τ]] r'[τ] θ'[τ])/Sqrt[a^2+r[τ]^2]-8 a^2 (℧^2-
2 r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[2 θ[τ]] t'[τ] θ'[τ]+8 r[τ] Sqrt[-℧^2+
2 r[τ]] Sqrt[a^2+r[τ]^2] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 θ'[τ]^2-8 a q ℧ Sqrt[-℧^2+
2 r[τ]] Sqrt[a^2+r[τ]^2] (-a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^2 φ'[τ]-
16 a (a^2 Cos[θ[τ]]^2+(℧^2-r[τ]) r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]]^2 r'[τ] φ'[τ]-
16 a Sqrt[-℧^2+2 r[τ]] (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) Sqrt[a^2+
r[τ]^2] Sin[θ[τ]]^2 t'[τ] φ'[τ]+16 a^3 Cos[θ[τ]] (℧^2-2 r[τ]) (a^2 Cos[θ[τ]]^2+
r[τ]^2) Sin[θ[τ]]^3 θ'[τ] φ'[τ]+Sqrt[-℧^2+2 r[τ]] Sqrt[a^2+r[τ]^2] (a^4+
a^4 Cos[4 θ[τ]] (-1+r[τ])+3 a^4 r[τ]+4 a^2 ℧^2 r[τ]-4 a^2 r[τ]^2+8 a^2 r[τ]^3+
8 r[τ]^5+4 a^2 Cos[2 θ[τ]] r[τ] (a^2-℧^2+r[τ]+2 r[τ]^2)) Sin[θ[τ]]^2 φ'[τ]^2)],
 
t'[0]  == dt0y/.initcon[[1]],
t[0]   == 0,
 
r''[τ] == Re[1/(8 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3) (-8 q ℧ Sqrt[-℧^2+2 r[τ]] Sqrt[a^2+
r[τ]^2] (-a^2 Cos[θ[τ]]^2+r[τ]^2) r'[τ]+(8 a^2 q ℧ Sqrt[-℧^2+2 r[τ]] (-a^2 Cos[θ[τ]]^2+
r[τ]^2) Sin[θ[τ]]^2 r'[τ])/Sqrt[a^2+r[τ]^2]+(4 (a^2 Cos[θ[τ]]^2+
r[τ]^2)^2 (a^2 Cos[2 θ[τ]] (-1+r[τ])-a^2 (1+r[τ])+2 r[τ] (-℧^2+r[τ])) r'[τ]^2)/(a^2+
r[τ]^2)-4 q ℧ (2 a^2 Cos[θ[τ]]^2-2 r[τ]^2) (a^2+r[τ]^2) (1+(℧^2-
2 r[τ])/(a^2 Cos[θ[τ]]^2+r[τ]^2)) t'[τ]+(8 a^2 q ℧ (℧^2-2 r[τ]) (a^2 Cos[θ[τ]]^2-
r[τ]^2) Sin[θ[τ]]^2 t'[τ])/(a^2 Cos[θ[τ]]^2+r[τ]^2)-(16 Sqrt[-℧^2+
2 r[τ]] (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2 Cos[θ[τ]]^2+
r[τ]^2) r'[τ] t'[τ])/Sqrt[a^2+r[τ]^2]+8 (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2+
℧^2-2 r[τ]+r[τ]^2) t'[τ]^2+8 a^2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 Sin[2 θ[τ]] r'[τ] θ'[τ]+
8 r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 (a^2+℧^2-2 r[τ]+r[τ]^2) θ'[τ]^2+(8 a q ℧ (℧^2-
2 r[τ]) (a^2 Cos[θ[τ]]^2-r[τ]^2) (a^2+r[τ]^2) Sin[θ[τ]]^2 φ'[τ])/(a^2 Cos[θ[τ]]^2+
r[τ]^2)-(4 a q ℧ (2 a^2 Cos[θ[τ]]^2-2 r[τ]^2) (-(a^2+r[τ]^2)^2 Sin[θ[τ]]^2+a^2 (a^2+
℧^2+(-2+r[τ]) r[τ]) Sin[θ[τ]]^4) φ'[τ])/(a^2 Cos[θ[τ]]^2+r[τ]^2)-(8 a Sqrt[-℧^2+
2 r[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2) (a^2 (-1+r[τ])+a^2 Cos[2 θ[τ]] (-1+r[τ])+
2 r[τ] (-℧^2+r[τ]+r[τ]^2)) Sin[θ[τ]]^2 r'[τ] φ'[τ])/Sqrt[a^2+r[τ]^2]-
16 a (a^2 Cos[θ[τ]]^2+(℧^2-r[τ]) r[τ]) (a^2+℧^2-2 r[τ]+
r[τ]^2) Sin[θ[τ]]^2 t'[τ] φ'[τ]+(a^2+℧^2-2 r[τ]+r[τ]^2) (a^4+a^4 Cos[4 θ[τ]] (-1+
r[τ])+3 a^4 r[τ]+4 a^2 ℧^2 r[τ]-4 a^2 r[τ]^2+8 a^2 r[τ]^3+8 r[τ]^5+
4 a^2 Cos[2 θ[τ]] r[τ] (a^2-℧^2+r[τ]+2 r[τ]^2)) Sin[θ[τ]]^2 φ'[τ]^2)],
 
r'[0]  == dr0y/.initcon[[1]],
r[0]   == r0,
 
θ''[τ] == Re[-1/(2 (a^2 Cos[θ[τ]]^2+r[τ]^2)^4) ((2 a^2 Cos[θ[τ]] (a^2 Cos[θ[τ]]^2+
r[τ]^2)^3 Sin[θ[τ]] r'[τ]^2)/(a^2+r[τ]^2)-2 a^2 q ℧ (℧^2-2 r[τ]) r[τ] Sin[2 θ[τ]] t'[τ]+
a^2 q ℧ r[τ] (a^2+2 ℧^2+a^2 Cos[2 θ[τ]]-4 r[τ]+2 r[τ]^2) Sin[2 θ[τ]] t'[τ]+
2 a^2 Cos[θ[τ]] (℧^2-2 r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[θ[τ]] t'[τ]^2+
4 r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2)^3 r'[τ] θ'[τ]-2 a^2 Cos[θ[τ]] (a^2 Cos[θ[τ]]^2+
r[τ]^2)^3 Sin[θ[τ]] θ'[τ]^2-4 a^3 q ℧ Cos[θ[τ]] (℧^2-2 r[τ]) r[τ] Sin[θ[τ]]^3 φ'[τ]+
4 a q ℧ Cot[θ[τ]] r[τ] (-(a^2+r[τ]^2)^2 Sin[θ[τ]]^2+a^2 (a^2+℧^2+(-2+
r[τ]) r[τ]) Sin[θ[τ]]^4) φ'[τ]+(2 a Sqrt[-℧^2+2 r[τ]] (a^2 Cos[θ[τ]]^2+
r[τ]^2)^3 Sin[2 θ[τ]] r'[τ] φ'[τ])/Sqrt[a^2+r[τ]^2]-2 a (℧^2-2 r[τ]) (a^2+
r[τ]^2) (a^2 Cos[θ[τ]]^2+r[τ]^2) Sin[2 θ[τ]] t'[τ] φ'[τ]+(a^2 Cos[θ[τ]]^2+
r[τ]^2) (2 a^2 Cos[θ[τ]] Sin[θ[τ]]^3 (-(a^2+r[τ]^2)^2+a^2 (a^2+℧^2+(-2+
r[τ]) r[τ]) Sin[θ[τ]]^2)+(a^2 Cos[θ[τ]]^2+r[τ]^2) (4 a^2 Cos[θ[τ]] (a^2+℧^2+
(-2+r[τ]) r[τ]) Sin[θ[τ]]^3-(a^2+r[τ]^2)^2 Sin[2 θ[τ]])) φ'[τ]^2)],
 
θ'[0]  == dθ0y/.initcon[[1]],
θ[0]   == θi,
 
φ''[τ] == Re[1/(4 (a^2 Cos[θ[τ]]^2+r[τ]^2)^3) ((4 a q ℧ (-a^4 Cos[θ[τ]]^4+r[τ]^4) r'[τ])/(a^2+
r[τ]^2)+(4 a (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) (a^2 Cos[θ[τ]]^2+
r[τ]^2)^2 r'[τ]^2)/(Sqrt[-℧^2+2 r[τ]] (a^2+r[τ]^2)^(3/2))+(4 a q ℧ Sqrt[-℧^2+
2 r[τ]] (-a^2 Cos[θ[τ]]^2+r[τ]^2) t'[τ])/Sqrt[a^2+r[τ]^2]+(8 a (a^2 Cos[θ[τ]]^2+(℧^2-
r[τ]) r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) r'[τ] t'[τ])/(a^2+r[τ]^2)+(4 a Sqrt[-℧^2+
2 r[τ]] (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-r[τ]^2) t'[τ]^2)/Sqrt[a^2+r[τ]^2]-
8 a q ℧ Cot[θ[τ]] r[τ] (a^2 Cos[θ[τ]]^2+r[τ]^2) θ'[τ]+(8 a Cot[θ[τ]] Sqrt[-℧^2+
2 r[τ]] (a^2 Cos[θ[τ]]^2+r[τ]^2)^2 r'[τ] θ'[τ])/Sqrt[a^2+r[τ]^2]-8 a Cot[θ[τ]] (℧^2-
2 r[τ]) (a^2 Cos[θ[τ]]^2+r[τ]^2) t'[τ] θ'[τ]+(4 a r[τ] Sqrt[-℧^2+2 r[τ]] (a^2 Cos[θ[τ]]^2+
r[τ]^2)^2 θ'[τ]^2)/Sqrt[a^2+r[τ]^2]-(4 a^2 q ℧ Sqrt[-℧^2+2 r[τ]] (-a^2 Cos[θ[τ]]^2+
r[τ]^2) Sin[θ[τ]]^2 φ'[τ])/Sqrt[a^2+r[τ]^2]+(8 (a^2 Cos[θ[τ]]^2+
r[τ]^2) (a^4 Cos[θ[τ]]^2 (-1+r[τ])-r[τ] (a^2 (a^2+℧^2-r[τ])+2 a^2 Cot[θ[τ]]^2 (a^2+
r[τ]^2)+Csc[θ[τ]]^2 (-a^4+r[τ]^4))) Sin[θ[τ]]^2 r'[τ] φ'[τ])/(a^2+r[τ]^2)-
(8 a^2 Sqrt[-℧^2+2 r[τ]] (a^2 Cos[θ[τ]]^2+℧^2 r[τ]-
r[τ]^2) Sin[θ[τ]]^2 t'[τ] φ'[τ])/Sqrt[a^2+r[τ]^2]-Cot[θ[τ]] (a^2 Cos[θ[τ]]^2+
r[τ]^2) (a^2 (3 a^2-4 ℧^2+4 (a^2+℧^2) Cos[2 θ[τ]]+a^2 Cos[4 θ[τ]])+
16 a^2 Cos[θ[τ]]^2 r[τ]^2+8 r[τ]^4+16 a^2 r[τ] Sin[θ[τ]]^2) θ'[τ] φ'[τ]+
(4 a Sqrt[-℧^2+2 r[τ]] Sin[θ[τ]]^2 (r[τ] (-a^4+r[τ]^4+a^2 (a^2+℧^2-r[τ]) Sin[θ[τ]]^2)+
Cos[θ[τ]]^2 (2 a^2 r[τ] (a^2+r[τ]^2)-a^4 (-1+r[τ]) Sin[θ[τ]]^2)) φ'[τ]^2)/Sqrt[a^2+r[τ]^2])],
 
φ'[0]  == dφ0y/.initcon[[1]],
φ[0]   == φ0,
 
WhenEvent[Abs[r[τ]] == N[R0]||Abs[r[τ]] > R0 &&
NumericQ[plunge6] == False,
(plunge6=τ) &&
(tt6=t[τ]) && (rt6=r[τ]) && (θt6=θ[τ]) && (φt6=φ[τ]);
"StopIntegration"],
 
WhenEvent[Abs[r[τ]] == N[R1] &&
NumericQ[plunge5] == False,
(plunge5=τ) && (tt5=t[τ]) && (rt5=r[τ]) && (θt5=θ[τ]) && (φt5=φ[τ]);
If[r0>R1, "StopIntegration"]],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && τ < -0.05 &&
NumericQ[plunge0] == False,
(plunge0=τ) &&
(tt0=t[τ]) && (rt0=r[τ]) && (θt0=θ[τ]) && (φt0=φ[τ]) &&
(δt0=t'[τ]) && (δr0=r'[τ]) && (δθ0=θ'[τ]) && (δφ0=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]>0 && τ < -0.05 &&
NumericQ[plunge1] == False,
(plunge1=τ) &&
(tt1=t[τ]) && (rt1=r[τ]) && (θt1=θ[τ]) && (φt1=φ[τ]) &&
(δt1=t'[τ]) && (δr1=r'[τ]) && (δθ1=θ'[τ]) && (δφ1=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]<0 && τ < -0.05 &&
NumericQ[plunge2] == False,
(plunge2=τ) &&
(tt2=t[τ]) && (rt2=r[τ]) && (θt2=θ[τ]) && (φt2=φ[τ]) &&
(δt2=t'[τ]) && (δr2=r'[τ]) && (δθ2=θ'[τ]) && (δφ2=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]>0 &&
τ < plunge1-0.05 &&
NumericQ[plunge3]==False && NumericQ[plunge1] == True,
(plunge3=τ) &&
(tt3=t[τ]) && (rt3=r[τ]) && (θt3=θ[τ]) && (φt3=φ[τ]) &&
(δt3=t'[τ]) && (δr3=r'[τ]) && (δθ3=θ'[τ]) && (δφ3=φ'[τ])],
 
WhenEvent[Mod[180/π Re[θ[τ]], 180] == 90.0 && r[τ]>N[si] &&
r[τ]<N[sr] && Re[θ'[τ]]<0 &&
τ < plunge2-0.05 &&
NumericQ[plunge4] == False && NumericQ[plunge2] == True,
(plunge4=τ) &&
(tt4=t[τ]) && (rt4=r[τ]) && (θt4=θ[τ]) && (φt4=φ[τ]) &&
(δt4=t'[τ]) && (δr4=r'[τ]) && (δθ4=θ'[τ]) && (δφ4=φ'[τ])]
 
}];
                                                                            (* Integrator *)
sol = TimeConstrained[If[NumericQ[dt0y /. initcon[[1]]] == False, {},
NDSolve[DGL, {t, r, θ, φ}, {τ, 0, tmax},
WorkingPrecision-> wp,
Method-> mta,
MaxSteps-> Infinity,
InterpolationOrder-> All,
StepMonitor :> (laststep=plunge7; plunge7=τ;
stepsize=plunge7-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-4, 0, 1])}
]], 10];
 
ft5h=If[NumericQ[plunge5], {φt5-π, θt5+π/2}, {0, -π/2}];
ft5b=If[NumericQ[plunge6], {φt6-π, θt6+π/2}, {0, -π/2}];
ft5x=If[NumericQ[plunge6], {0, 1}, {0, 0}];
ft5y=If[NumericQ[plunge5], {0, 1}, {0, 0}];
 
ft0s=If[NumericQ[plunge0], {φt0, rt0}, {π, sr}];
ft1s=If[NumericQ[plunge1], {φt1, rt1}, {π, sr}];
ft2s=If[NumericQ[plunge2], {φt2, rt2}, {π, sr}];
ft3s=If[NumericQ[plunge3], {φt3, rt3}, {π, sr}];
ft4s=If[NumericQ[plunge4], {φt4, rt4}, {π, sr}];
 
ft0v=If[NumericQ[plunge0], {-dφv[rt0, tt0+t0+rT], 0}, {0, 0}];
ft1v=If[NumericQ[plunge1], {-dφv[rt1, tt1+t0+rT], 0}, {0, 0}];
ft2v=If[NumericQ[plunge2], {-dφv[rt2, tt2+t0+rT], 0}, {0, 0}];
ft3v=If[NumericQ[plunge3], {-dφv[rt3, tt3+t0+rT], 0}, {0, 0}];
ft4v=If[NumericQ[plunge4], {-dφv[rt4, tt4+t0+rT], 0}, {0, 0}];
ft5v=If[NumericQ[plunge5], {-(tt5+t0+rT) ωR1, 0}, {0, 0}];
 
ft0f=If[NumericQ[plunge0], {0, Min[fmax, shF shf[rt0, δt0, δr0, δθ0, δφ0]]}, {0, 0}];
ft1f=If[NumericQ[plunge1], {0, Min[fmax, shF shf[rt1, δt1, δr1, δθ1, δφ1]]}, {0, 0}];
ft2f=If[NumericQ[plunge2], {0, Min[fmax, shF shf[rt2, δt2, δr2, δθ2, δφ2]]}, {0, 0}];
ft3f=If[NumericQ[plunge3], {0, Min[fmax, shF shf[rt3, δt3, δr3, δθ3, δφ3]]}, {0, 0}];
ft4f=If[NumericQ[plunge4], {0, Min[fmax, shF shf[rt4, δt4, δr4, δθ4, δφ4]]}, {0, 0}];
ft5f={0, Min[fmax, ς shF]};

ft0F=If[NumericQ[plunge0], {0, Min[fmax, ShF shf[rt0, δt0, δr0, δθ0, δφ0]]}, {0, 0}];
ft1F=If[NumericQ[plunge1], {0, Min[fmax, ShF shf[rt1, δt1, δr1, δθ1, δφ1]]}, {0, 0}];
ft2F=If[NumericQ[plunge2], {0, Min[fmax, ShF shf[rt2, δt2, δr2, δθ2, δφ2]]}, {0, 0}];
ft3F=If[NumericQ[plunge3], {0, Min[fmax, ShF shf[rt3, δt3, δr3, δθ3, δφ3]]}, {0, 0}];
ft4F=If[NumericQ[plunge4], {0, Min[fmax, ShF shf[rt4, δt4, δr4, δθ4, δφ4]]}, {0, 0}];
ft5F={0, Min[fmax, ς ShF]};
{
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0s+ft0v, ft1s+ft1v, ft2s+ft2v, ft3s+ft3v, ft4s+ft4v,
ft0f, ft1f, ft2f, ft3f, ft4f,
ft5h+ft5v, ft5b, ft5f, ft5x, ft5y,
ft0F, ft1F, ft2F, ft3F, ft4F, ft5F
}]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 10) Memoryfunktion ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
mem : raytrace[{Ф_, ϑ_}] := mem = Quiet[Re[raytracer[{Ф, ϑ}]]];
 
ray01[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[01]];
ray02[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[02]];
ray03[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[03]];
ray04[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[04]];
ray05[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[05]];
 
ray06[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[06]];
ray07[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[07]];
ray08[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[08]];
ray09[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[09]];
ray10[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[10]];
 
ray11[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[11]];
ray12[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[12]];
ray13[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[13]];
ray14[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[14]];
ray15[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[15]];
 
ray16[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[16]];
ray17[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[17]];
ray18[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[18]];
ray19[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[19]];
ray20[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[20]];

ray21[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[21]];
ray22[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[22]];
ray23[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[23]];
ray24[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[24]];
ray25[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[25]];
ray26[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[26]];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 11) Proportionen ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
width1  = ImageDimensions[pic1][[1]]; height1 = ImageDimensions[pic1][[2]];
width2  = ImageDimensions[pic2][[1]]; height2 = ImageDimensions[pic2][[2]];
width3  = ImageDimensions[pic3][[1]]; height3 = ImageDimensions[pic3][[2]];
width4  = ImageDimensions[pic4][[1]]; height4 = ImageDimensions[pic4][[2]];
width5  = ImageDimensions[pic5][[1]]; height5 = ImageDimensions[pic5][[2]];
width6  = ImageDimensions[pic7][[1]]; height6 = ImageDimensions[pic7][[2]];
hzoom   = If[breite>2 hoehe, 1/zoom, 1/zoom/2/hoehe*breite];
vzoom   = If[breite>2 hoehe, 1/zoom*2 hoehe/breite, 1/zoom];
 
"Geschätzte Rechenzeit" -> 1.2 (AbsoluteTiming[Do[raytracer[{
RandomReal[{-π, π}]/zoom, RandomReal[{-π/2, π/2}]/zoom
}], {ü, 1, 50}]][[1]])/50*hoehe*breite/kernels/60 "Minuten"
 
FOV->{360.0 hzoom "degree", 180.0 vzoom "degree"}
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 12) Output ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
img = ParallelTable[{
 
(* 1 Hintergrundpanorama *)
Quiet@ImageTransformation[pct1, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width1},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 2 Sphäre *)
Quiet@ImageTransformation[pct2, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-3π/2, π/2-2π/width2},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 3 Scheibe Textur komplett *)
Quiet@ImageTransformation[pic3, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 4 Scheibe Textur Front *)
Quiet@ImageTransformation[pic3, ray02, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 5 Scheibe Textur Echo 1 *)
Quiet@ImageTransformation[pic3, ray03, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 6 Scheibe Textur Echo 2 *)
Quiet@ImageTransformation[pic3, ray04, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 7 Scheibe Textur Echo 3 *)
Quiet@ImageTransformation[pic3, ray05, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 8 Scheibe Geometrie still komplett *)
Quiet@ImageTransformation[pic4, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 9 Scheibe Geometrie still Front *)
Quiet@ImageTransformation[pic4, ray02, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 10 Scheibe Geometrie still Echo 1 *)
Quiet@ImageTransformation[pic4, ray03, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 11 Scheibe Geometrie still Echo 2 *)
Quiet@ImageTransformation[pic4, ray04, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 12 Scheibe Geometrie still Echo 3 *)
Quiet@ImageTransformation[pic4, ray05, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 13 Scheibe Geometrie rotierend komplett *)
Quiet@ImageTransformation[pic4, ray06, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 14 Scheibe Geometrie rotierend Front *)
Quiet@ImageTransformation[pic4, ray07, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 15 Scheibe Geometrie rotierend Echo 1 *)
Quiet@ImageTransformation[pic4, ray08, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 16 Scheibe Geometrie rotierend Echo 2 *)
Quiet@ImageTransformation[pic4, ray09, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 17 Scheibe Geometrie rotierend Echo 3 *)
Quiet@ImageTransformation[pic4, ray10, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 18 Frequenzverschiebung komplett SW *)
Quiet@ImageTransformation[pic5, ray11, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-1, 1},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 19 Frequenzverschiebung Front SW *)
Quiet@ImageTransformation[pic5, ray12, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 20 Frequenzverschiebung Echo 1 SW *)
Quiet@ImageTransformation[pic5, ray13, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 21 Frequenzverschiebung Echo 2 SW *)
Quiet@ImageTransformation[pic5, ray14, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 22 Frequenzverschiebung Echo 3 SW *)
Quiet@ImageTransformation[pic5, ray15, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 23 Frequenzverschiebung komplett Farbe *)
Quiet@ImageTransformation[pic6, ray11, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 24 Frequenzverschiebung Front Farbe *)
Quiet@ImageTransformation[pic6, ray12, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 25 Frequenzverschiebung Echo 1 Farbe *)
Quiet@ImageTransformation[pic6, ray13, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 26 Frequenzverschiebung Echo 2 Farbe *)
Quiet@ImageTransformation[pic6, ray14, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 27 Frequenzverschiebung Echo 3 Farbe *)
Quiet@ImageTransformation[pic6, ray15, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 28 Hintergrundpanorama *)
ImageTransformation[pct3, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width6},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 29 Sphäre *)
ImageTransformation[pct3, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width6},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 30 Scheibe Textur komplett *)
ImageTransformation[pic7, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width6},
{si, sr+(sr-si)/height6}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 31 Frequenzverschiebung Hintergrund Farbe *)
Quiet@ImageTransformation[pic6, ray18, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 32 Frequenzverschiebung Hintergrund SW *)
Quiet@ImageTransformation[pic5, ray18, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 33 Kontur BH *)
Quiet@ImageTransformation[pic5, ray19, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 34 Kontur IH *)
Quiet@ImageTransformation[pic5, ray20, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{0, 1}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 35 Frequenzverschiebung komplett SW *)
Quiet@ImageTransformation[pic5, ray21, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-1, 1},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 36 Frequenzverschiebung Front SW *)
Quiet@ImageTransformation[pic5, ray22, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 37 Frequenzverschiebung Echo 1 SW *)
Quiet@ImageTransformation[pic5, ray23, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 38 Frequenzverschiebung Echo 2 SW *)
Quiet@ImageTransformation[pic5, ray24, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 39 Frequenzverschiebung Echo 3 SW *)
Quiet@ImageTransformation[pic5, ray25, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 40 Frequenzverschiebung komplett Farbe *)
Quiet@ImageTransformation[pic6, ray21, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 41 Frequenzverschiebung Front Farbe *)
Quiet@ImageTransformation[pic6, ray22, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 42 Frequenzverschiebung Echo 1 Farbe *)
Quiet@ImageTransformation[pic6, ray23, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 43 Frequenzverschiebung Echo 2 Farbe *)
Quiet@ImageTransformation[pic6, ray24, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],
 
(* 44 Frequenzverschiebung Echo 3 Farbe *)
Quiet@ImageTransformation[pic6, ray25, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 45 Frequenzverschiebung Hintergrund Farbe *)
Quiet@ImageTransformation[pic6, ray26, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"],

(* 46 Frequenzverschiebung Hintergrund SW *)
Quiet@ImageTransformation[pic5, ray26, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π},
{fmin, fmax}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Fixed"]
 
}, {x, 0, π-π/kernels/grain, π/kernels/grain}];
 
image[num_] := ImageAssemble[Table[{img[[x, num]]}, {x, kernels grain, 1, -1}]];
fi[x_] := ColorNegate[x];
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 13) Composite |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
Table[image[n], {n, 1, 46, 1}]

gr2 = ImageMultiply[fi@image[19], fi@image[20]];
Gr2 = ImageMultiply[fi@image[36], fi@image[37]];
gr3 = ImageMultiply[fi@image[21], fi@image[22]];
Gr3 = ImageMultiply[fi@image[38], fi@image[39]];
ds2 = ImageMultiply[fi@image[09], fi@image[10]];
ds3 = ImageMultiply[fi@image[11], fi@image[12]];
ds6 = ImageMultiply[fi@image[14], fi@image[15]];
ds7 = ImageMultiply[fi@image[16], fi@image[17]];
se2 = ImageMultiply[fi@image[04], fi@image[05]];
se3 = ImageMultiply[fi@image[06], fi@image[07]];
sea = ImageMultiply[image[04], image[19]];
seb = ImageMultiply[image[05], image[20]];
sec = ImageMultiply[image[06], image[21]];
sed = ImageMultiply[image[07], image[22]];
seA = ImageMultiply[image[04], image[36]];
seB = ImageMultiply[image[05], image[37]];
seC = ImageMultiply[image[06], image[38]];
seD = ImageMultiply[image[07], image[39]];
bl2 = ImageMultiply[fi@image[24], fi@image[25]];
bl3 = ImageMultiply[fi@image[26], fi@image[27]];
Bl2 = ImageMultiply[fi@image[41], fi@image[42]];
Bl3 = ImageMultiply[fi@image[43], fi@image[44]];
se5 = ImageMultiply[fi@sea, fi@seb];
se6 = ImageMultiply[fi@sec, fi@sed];
Se5 = ImageMultiply[fi@seA, fi@seB];
Se6 = ImageMultiply[fi@seC, fi@seD];

"Lösung 1, v local" == vsolve[[1, 1]]/.dtf->"dt"/.vrf->"vr"/.vφf->"vφ"/.vϑf->"vϑ"/.v0f->"v0"

"Lösung 2, v local" == vsolve[[2, 1]]/.dtf->"dt"/.vrf->"vr"/.vφf->"vφ"/.vϑf->"vϑ"/.v0f->"v0"

"Meistens gilt Lösung 1, im Bereich der Ergosphäre manchmal Lösung 2"

"äußere Kontur"
bf3 = image[33]

"innere Kontur"
bf4 = image[34]

"Hintergrund, Milchstraße"
bkg = image[1]

"Hintergrund, Checkerboard"
cb1 = image[28]

"Horizont, Schale"
hrz = image[2]

"Horizont, Checkerboard"
cb2 = image[29]

"statische Checkerboard Scheibe, Geometrie"
cb3 = image[30]

"statische undurchsichtige Scheibe, Geometrie"
ds1 = image[8]

"statische transparente Scheibe, Geometrie"
ds4 = fi@ImageMultiply[ds2, ds3]

"rotierende undurchsichtige Scheibe, Geometrie"
ds5 = image[13]

"rotierende transparente Scheibe, Geometrie"
ds8 = fi@ImageMultiply[ds6, ds7]

"Scheibe, Textur, undurchsichtig"
se1 = image[03]

"Scheibe, Textur, transparent"
se4 = fi@ImageMultiply[se2, se3]

"Frequenzverschiebung Hintergrund, Farbe, Lösung 1"
bf1 = image[31]

"Frequenzverschiebung Hintergrund, SW, Lösung 1"
bf2 = image[32]

"Scheibe, Textur, transparent, Helligkeit A, Lösung 1"
se7 = fi@ImageMultiply[se5, se6]

"Scheibe, Textur, transparent, Helligkeit B, Lösung 1"
se8 = fi@ImageMultiply[fi@se7, fi@se7]

"Scheibe, Textur, transparent, Helligkeit C, Lösung 1"
se9 = fi@ImageMultiply[fi@se8, fi@se7]

"Frequenzverschiebung, Farbe, undurchsichte Scheibe, Lösung 1"
bl1 = image[23]

"Frequenzverschiebung, Farbe, transparente Scheibe, Lösung 1"
bl4 = fi@ImageMultiply[bl2, bl3]

"Frequenzverschiebung, undurchsichtige Scheibe, SW, Lösung 1"
gr1 = image[18]

"Frequenzverschiebung, transparente Scheibe, SW, Lösung 1"
gr4 = fi@ImageMultiply[gr2, gr3]

"Frequenzverschiebung Hintergrund, Farbe, Lösung 2"
Bf1 = image[45]

"Frequenzverschiebung Hintergrund, SW, Lösung 2"
Bf2 = image[46]

"Scheibe, Textur, transparent, Helligkeit A, Lösung 2"
Se7 = fi@ImageMultiply[Se5, Se6]

"Scheibe, Textur, transparent, Helligkeit B, Lösung 2"
Se8 = fi@ImageMultiply[fi@Se7, fi@Se7]

"Scheibe, Textur, transparent, Helligkeit C, Lösung 2"
Se9 = fi@ImageMultiply[fi@Se8, fi@Se7]

"Frequenzverschiebung, Farbe, undurchsichte Scheibe, Lösung 2"
Bl1 = image[40]

"Frequenzverschiebung, Farbe, transparente Scheibe, Lösung 2"
Bl4 = fi@ImageMultiply[Bl2, Bl3]

"Frequenzverschiebung, undurchsichtige Scheibe, SW, Lösung 2"
Gr1 = image[35]

"Frequenzverschiebung, transparente Scheibe, SW, Lösung 2"
Gr4 = fi@ImageMultiply[Gr2, Gr3]
 
Quit[]









Transformation des Outputs im Plattkartenformat in die stereographische Projektion:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* > raytracing.yukterez.net | Equirectangular -> Stereographic Projection Transformation *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

size = 377;

xyz[{x_, y_}]    := {Sin[y] Cos[x], Sin[y] Sin[x], Cos[y]}
xy[{x_, y_, z_}] := {ArcTan[x, y], ArcCos[z]}

Xyz[{x_, y_, z_}, α_] := {x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z}
xYz[{x_, y_, z_}, β_] := {x Cos[β]+z Sin[β], y,                 z Cos[β]-x Sin[β]}
xyZ[{x_, y_, z_}, ψ_] := {x,                 y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]}

rm[pic_, α_, β_, ψ_] := xy[xyZ[xYz[Xyz[xyz[pic], α], β], ψ]]
RM[{x_, y_}] := rm[{x, y}, α, β, ψ]

Eq2St[{x_, y_}] := {0+ArcTan[-y, x], -2 ArcTan[2, Sqrt[x^2+y^2]]+π/2};
eq2st[{x_, y_}] := RM[Eq2St[{x, y}]+{0, Pi/2}]-{0, Pi/2}

Eq = Import["http://www.yukterez.net/mw/testdisk.png"]

pic := ImageTransformation[Eq, eq2st, {size, size},
       DataRange -> {{-π, π}, {-π/2, π/2}},
       PlotRange -> {{-2, 2}, {-2, 2}}, Padding -> "Fixed", Resampling -> "Nearest"];
     
α=0; β=-π/2; ψ=0;
pic1 = pic

α=0; β=+π/2; ψ=0;
pic2 = ImageRotate[pic, π]
     
Export["pic1.png", pic1]
Export["pic2.png", pic2]










Für den Umrechner der Lokalgeschwindigkeit vom einen System ins andere klick hier. Beispiel mit a=℧=0.3, θ=85°, r=50, ri=isco=4.826, ra=10:



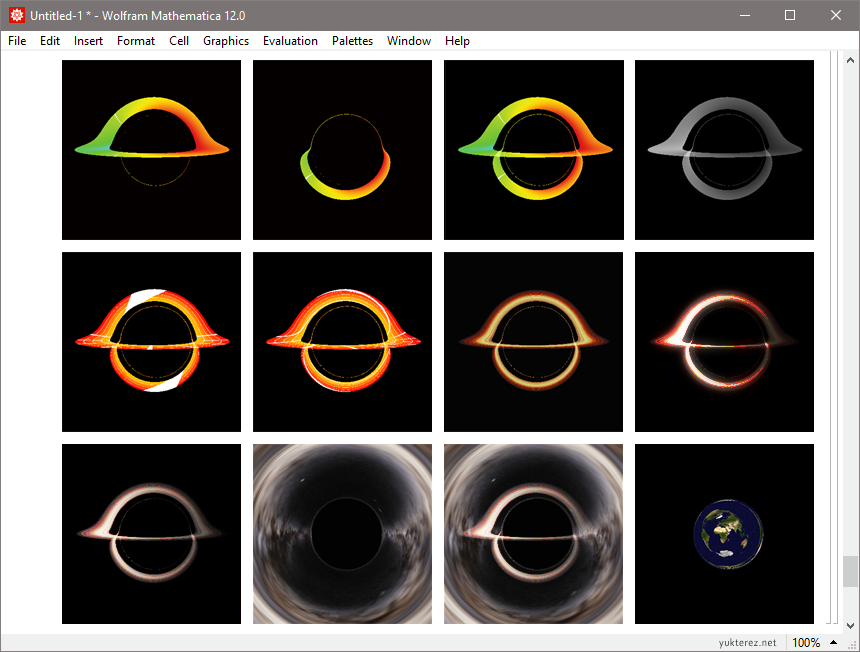
Minkowski Raytracer:

Code: Alles auswählen

(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* > raytracing.yukterez.net | 07.04.2018 - 09.09.2020 | Version 20 | Simon Tyran, Vienna *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)

Pause[1]                                                         (* Minkowski Koordinaten *)

wp  = MachinePrecision;
mt0 = Automatic;
mt1 = {"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mta = mt0;                                (* mt0 für Geschwindigkeit, mt1 für Genauigkeit *)
                                       
kernels = 6;                                                          (* Parallelisierung *)
grain   = 5;                            (* Subparallelisierung auf kernels*grain Streifen *)
rsp     = "Nearest";                                                        (* Resampling *)

breite  = 240;                                               (* Zielabmessungen in Pixeln *)
hoehe   = 120;          (* Höhe sollte ein ganzzahliges Vielfaches von kernels*grain sein *)
zoom    = 1;                                  (* doppelter Zoom ergibt halben Sichtwinkel *)
 
LaunchKernels[kernels]
wp = MachinePrecision;                                                     (* Genauigkeit *)
 
pic1 = Import["http://www.yukterez.net/mw/1/flip70.png"];    (* Hintergrundpanorama laden *)
pic2 = Import["http://www.yukterez.net/mw/1/worldmap.png"];    (* Sphärenoberfläche laden *)
pic3 = Import["http://www.yukterez.net/mw/akkretionsscheibe.jpg"];(* Scheibentextur laden *)
pic4 = Import["http://www.yukterez.net/mw/disk.png"];          (* Scheibengeometrie laden *)
pic7 = Import["http://www.yukterez.net/mw/1/cl.png"];               (* Checkerboard laden *)
 
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* 1) Startbedingungen und Position des Beobachters ||||||||||||||||||||||||||||||||||||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
 
r0   = 10;                                            (* Radialkoordinate des Beobachters *)
R0   = 500;                              (* Radius des umspannenden Kugelschalenpanoramas *)
R1   = 1+1/(5 Sqrt[2]);                                                         (* Sphäre *)
si   = 1.6367824;                                        (* Akkretionsscheibe Innenradius *)
sr   = 7;                                                (* Akkretionsscheibe Außenradius *)
θ0   = 70 π/180;                                                           (* Breitengrad *)
φ0   = 0;                                                                   (* Längengrad *)
t0 = 0;                                                      (* Eigenzeit des Beobachters *)
 
tmax =-3 R0;                                            (* zeitlicher Integrationsbereich *)
 
vr   = 0;                                      (* Radiale Geschwindigkeit des Beobachters *)
vϑ   = 0;                                       (* Polare Geschwindigkeit des Beobachters *)
vφ   = 0;                                    (* Azimutale Geschwindigkeit des Beobachters *)

vL   = Sqrt[vr^2+vϑ^2+vφ^2];

hvs  = 0; (* ArcSin[vφ/vL] *)                        (* horizontaler Versatz in Radianten *)
vvs  = 0; (* ArcSin[vϑ/vL] *)                          (* vertikaler Versatz in Radianten *)
 
fpt[{x_, y_}] := {If[y<0, x+1, x], If[y<0, -y, y]}
 
pcr1 = ParallelTable[
ImageTransformation[pic1, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct1 = ImageAssemble[Table[{pcr1[[x]]}, {x, 2 kernels, 1, -1}]];
 
pcr2 = ParallelTable[
ImageTransformation[pic2, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct2 = ImageAssemble[Table[{pcr2[[x]]}, {x, 2 kernels, 1, -1}]];

pcr3 = ParallelTable[
ImageTransformation[pic7, fpt, DataRange->{{-1, 1}, {0, 1}},
PlotRange->{{-1, 1}, {-1+(x-1)/kernels, -1+x/kernels}}, Resampling->rsp, Padding->"Periodic"],
{x, 1, 2 kernels}];
pct3 = ImageAssemble[Table[{pcr3[[x]]}, {x, 2 kernels, 1, -1}]];

a = 0; ℧ = 0; v0 = 1; q = 0; st = 0.01; vϑ = 0;
 
vθ  =-vϑ;
θs  = π/2;
θi  =-θ0+π;
θ1  = θi;

dφv[rt_, tt_] := 0;
shf[rt_, δt_, δr_, δθ_, δφ_] := 1;
ωφ = -vφ Csc[θ1]/r0;
ωθ = -vϑ/r0;

gtt = -1;
grr = +1;
gθθ = +r0^2;
gφφ = +r0^2 Sin[θ1]^2;
gtφ = +0;
 
ς = 1;
j[v_] := Sqrt[1-v^2];
nq[x_] := If[NumericQ[x], If[Element[x, Reals], x, 0], 0];

U = {+vr, +vθ, +vφ};
γ = 1/Sqrt[1-Norm[U]^2];
 
Xyz[{x_, y_, z_}, α_] := {x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z};
xYz[{x_, y_, z_}, β_] := {x Cos[β]+z Sin[β], y, z Cos[β]-x Sin[β]};
xyZ[{x_, y_, z_}, ψ_] := {x, y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]};
 
raytracer[{Ф_, ϑ_}] :=
 
Quiet[Module[{DGL, sol, εj, pθi, pr0, Q, k, V, W, vw,
vr0i, vθ0i, vφ0i, vr0n, vθ0n, vφ0n, vr0a, vθia, vφ0a, vt0a,
t10, r10, Θ10, Φ10, t, r, θ, φ, τ,
т, т0, т1, т2, т3, т4, т5,
plunge, plunge0, plunge1, plunge2, plunge3,
plunge4, plunge5, plunge6, plunge7,
dθ0, dφ0, δφ0, δθ0, δr0, δt0, tt0, rt0, θt0, φt0,
dθ1, dφ1, δφ1, δθ1, δr1, δt1, tt1, rt1, θt1, φt1,
dθ2, dφ2, δφ2, δθ2, δr2, δt2, tt2, rt2, θt2, φt2,
dθ3, dφ3, δφ3, δθ3, δr3, δt3, tt3, rt3, θt3, φt3,
dθ4, dφ4, δφ4, δθ4, δr4, δt4, tt4, rt4, θt4, φt4,
dθ5, dφ5, δφ5, δθ5, δr5, δt5, tt5, rt5, θt5, φt5,
dθ6, dφ6, δφ6, δθ6, δr6, δt6, tt6, rt6, θt6, φt6,
X, Y, Z, ξ, stepsize, laststep, mtl, ft, fτ, varb,
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0v, ft1v, ft2v, ft3v, ft4v, ft5v,
ft0f, ft1f, ft2f, ft3f, ft4f,
ft5h, ft5b, ft5f},
 
vw=xyZ[Xyz[{0, 1, 0}, ϑ], Ф+π/2];
                                 (* Übersetzung des Einfallswinkels in den lokalen Tetrad *)
vr0a = vw[[3]];
vφ0a = vw[[2]];
vθia = vw[[1]];
                                                                                (* Betrag *)
vt0a = Sqrt[vr0a^2+vφ0a^2+vθia^2];
                                                                            (* Normierung *)
vr0n = vr0a/vt0a;
vφ0n = vφ0a/vt0a;
vθ0n = vθia/vt0a;
                                              (* Relativistische Geschwindigkeitsaddition *)
V={vr0n, vθ0n, vφ0n};
W=(U+V+γ/(1+γ)(U\[Cross](U\[Cross]V)))/(1+U.V);
                                                                            (* Aberration *)
vr0i = W[[1]];
vθ0i = W[[2]];
vφ0i = W[[3]];
                     
DGL = {                                                 (* Minkowski Bewegungsgleichungen *)
 
t''[τ] == 0,
t'[0]  == 1,
t[0]   == 0,
 
r''[τ] == r[τ](θ'[τ]^2+Sin[θ[τ]]^2 φ'[τ]^2),
r'[0]  == vr0i,
r[0]   == r0,
 
θ''[τ] == Sin[θ[τ]] Cos[θ[τ]] φ'[τ]^2-2 θ'[τ] r'[τ]/r[τ],
θ'[0]  == vθ0i/r0,
θ[0]   == θi,
 
φ''[τ] == -2 φ'[τ] (r'[τ]+r[τ] θ'[τ] Cot[θ[τ]])/r[τ],
φ'[0]  == vφ0i Csc[θ1]/r0,
φ[0]   == φ0,
 
WhenEvent[Mod[θ[τ], π] == π/2.0 && r[τ]>si && r[τ]<sr &&
NumericQ[plunge0] == False,
(plunge0=τ) &&
(tt0=t[τ]) && (rt0=r[τ]) && (θt0=θ[τ]) && (φt0=φ[τ]) &&
(δt0=t'[τ]) && (δr0=r'[τ]) && (δθ0=θ'[τ]) && (δφ0=φ'[τ])],
 
WhenEvent[Mod[θ[τ], π] == π/2.0 && r[τ]>si && r[τ]<sr && Re[θ'[τ]]>0 &&
NumericQ[plunge1] == False,
(plunge1=τ) &&
(tt1=t[τ]) && (rt1=r[τ]) && (θt1=θ[τ]) && (φt1=φ[τ]) &&
(δt1=t'[τ]) && (δr1=r'[τ]) && (δθ1=θ'[τ]) && (δφ1=φ'[τ])],
 
WhenEvent[Mod[θ[τ], π] == π/2.0 && r[τ]>si && r[τ]<sr && Re[θ'[τ]]<0 &&
NumericQ[plunge2] == False,
(plunge2=τ) &&
(tt2=t[τ]) && (rt2=r[τ]) && (θt2=θ[τ]) && (φt2=φ[τ]) &&
(δt2=t'[τ]) && (δr2=r'[τ]) && (δθ2=θ'[τ]) && (δφ2=φ'[τ])],
 
WhenEvent[Mod[θ[τ], π] == π/2.0 && r[τ]>si && r[τ]<sr && Re[θ'[τ]]>0 &&
τ < plunge1-0.05 &&
NumericQ[plunge3]==False && NumericQ[plunge1] == True,
(plunge3=τ) &&
(tt3=t[τ]) && (rt3=r[τ]) && (θt3=θ[τ]) && (φt3=φ[τ]) &&
(δt3=t'[τ]) && (δr3=r'[τ]) && (δθ3=θ'[τ]) && (δφ3=φ'[τ])],
 
WhenEvent[Mod[θ[τ], π] == π/2.0 && r[τ]>si && r[τ]<sr && Re[θ'[τ]]<0 &&
τ < plunge2-0.05 &&
NumericQ[plunge4] == False && NumericQ[plunge2] == True,
(plunge4=τ) &&
(tt4=t[τ]) && (rt4=r[τ]) && (θt4=θ[τ]) && (φt4=φ[τ]) &&
(δt4=t'[τ]) && (δr4=r'[τ]) && (δθ4=θ'[τ]) && (δφ4=φ'[τ])],
 
WhenEvent[Abs[r[τ]] == N@R1 &&
NumericQ[plunge5] == False,
(plunge5=τ) && (tt5=t[τ]) && (rt5=r[τ]) && (θt5=θ[τ]) && (φt5=φ[τ]);
If[r0>R1, "StopIntegration"]],
 
WhenEvent[Abs[r[τ]] == R0||r[τ]>R0 &&
NumericQ[plunge6] == False,
(plunge6=τ) &&
(tt6=t[τ]) && (rt6=r[τ]) && (θt6=θ[τ]) && (φt6=φ[τ]);
"StopIntegration"]
 
};
                                                                            (* Integrator *)
sol = TimeConstrained[NDSolve[DGL, {t, r, θ, φ}, {τ, 0, tmax},
WorkingPrecision-> wp,
Method-> mta,
MaxSteps-> Infinity,
StepMonitor :> (laststep=plunge7; plunge7=τ;
stepsize=plunge7-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-4, 0, 1])}
], 10];
 
ft0s=If[NumericQ[plunge0], If[rt0>sr, {π, sr},
If[rt0<si, {π, sr}, {φt0+(tt0+r0) ωφ, rt0}]], {π, sr}];
ft1s=If[NumericQ[plunge1], If[rt1>sr, {π, sr},
If[rt1<si, {π, sr}, {φt1+(tt1+r0) ωφ, rt1}]], {π, sr}];
ft2s=If[NumericQ[plunge2], If[rt2>sr, {π, sr},
If[rt2<si, {π, sr}, {φt2+(tt2+r0) ωφ, rt2}]], {π, sr}];
ft3s=If[NumericQ[plunge3], If[rt3>sr, {π, sr},
If[rt3<si, {π, sr}, {φt3+(tt3+r0) ωφ, rt3}]], {π, sr}];
ft4s=If[NumericQ[plunge4], If[rt4>sr, {π, sr},
If[rt4<si, {π, sr}, {φt4+(tt4+r0) ωφ, rt4}]], {π, sr}];
 
ft0v=If[NumericQ[plunge0], If[rt0>sr, {0, 0},
If[rt0<si, {0, 0}, {-dφv[rt0, tt0+t0], 0}]], {0, 0}];
ft1v=If[NumericQ[plunge1], If[rt1>sr, {0, 0},
If[rt1<si, {0, 0}, {-dφv[rt1, tt1+t0], 0}]], {0, 0}];
ft2v=If[NumericQ[plunge2], If[rt2>sr, {0, 0},
If[rt2<si, {0, 0}, {-dφv[rt2, tt2+t0], 0}]], {0, 0}];
ft3v=If[NumericQ[plunge3], If[rt3>sr, {0, 0},
If[rt3<si, {0, 0}, {-dφv[rt3, tt3+t0], 0}]], {0, 0}];
ft4v=If[NumericQ[plunge4], If[rt4>sr, {0, 0},
If[rt4<si, {0, 0}, {-dφv[rt4, tt4+t0], 0}]], {0, 0}];
 
ft0f=If[NumericQ[plunge0], If[rt0>sr, {0, 0},
If[rt0<si, {0, 0}, {0, Min[2, shf[rt0, δt0, δr0, δθ0, δφ0]]}]], {0, 0}];
ft1f=If[NumericQ[plunge1], If[rt1>sr, {0, 0},
If[rt1<si, {0, 0}, {0, Min[2, shf[rt1, δt1, δr1, δθ1, δφ1]]}]], {0, 0}];
ft2f=If[NumericQ[plunge2], If[rt2>sr, {0, 0},
If[rt2<si, {0, 0}, {0, Min[2, shf[rt2, δt2, δr2, δθ2, δφ2]]}]], {0, 0}];
ft3f=If[NumericQ[plunge3], If[rt3>sr, {0, 0},
If[rt3<si, {0, 0}, {0, Min[2, shf[rt3, δt3, δr3, δθ3, δφ3]]}]], {0, 0}];
ft4f=If[NumericQ[plunge4], If[rt4>sr, {0, 0},
If[rt4<si, {0, 0}, {0, Min[2, shf[rt4, δt4, δr4, δθ4, δφ4]]}]], {0, 0}];
 
ft5h=If[NumericQ[plunge5], {φt5-π, θt5+π/2}, {0, -π/2}];
ft5b=If[NumericQ[plunge6], If[rt6<If[Element[R1, Reals], R1, 0], {0, -π/2},
If[rt6>4 R0, {0, -π/2}, {φt6-π, θt6+π/2}]], {0, -π/2}];
 
{
ft0s, ft1s, ft2s, ft3s, ft4s,
ft0s+ft0v, ft1s+ft1v, ft2s+ft2v, ft3s+ft3v, ft4s+ft4v,
ft0f, ft1f, ft2f, ft3f, ft4f,
ft5h, ft5b
}]];
 
mem : raytrace[{Ф_, ϑ_}] := mem = Quiet[Re[raytracer[{Ф, ϑ}]]];
 
ray01[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[01]];
ray02[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[02]];
ray03[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[03]];
ray04[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[04]];
ray05[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[05]];
 
ray06[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[06]];
ray07[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[07]];
ray08[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[08]];
ray09[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[09]];
ray10[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[10]];
 
ray11[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[11]];
ray12[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[12]];
ray13[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[13]];
ray14[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[14]];
ray15[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[15]];
 
ray16[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[16]];
ray17[{Ф_, ϑ_}] := raytrace[{Ф, ϑ}][[17]];
 
width1  = ImageDimensions[pic1][[1]]; height1 = ImageDimensions[pic1][[2]];
width2  = ImageDimensions[pic2][[1]]; height2 = ImageDimensions[pic2][[2]];
width3  = ImageDimensions[pic3][[1]]; height3 = ImageDimensions[pic3][[2]];
width4  = ImageDimensions[pic4][[1]]; height4 = ImageDimensions[pic4][[2]];
width5  = ImageDimensions[pic7][[1]]; height5 = ImageDimensions[pic7][[2]];

hzoom   = If[breite>2 hoehe, 1/zoom, 1/zoom/2/hoehe*breite];
vzoom   = If[breite>2 hoehe, 1/zoom*2 hoehe/breite, 1/zoom];

"Geschätzte Rechenzeit" -> 1.2 (AbsoluteTiming[Do[raytracer[{
RandomReal[{-π, π}]/zoom, RandomReal[{-π/2, π/2}]/zoom
}], {ü, 1, 50}]][[1]])/50*hoehe*breite/kernels/60 "Minuten"
 
FOV->{360.0 hzoom "degree", 180.0 vzoom "degree"}
 
img = ParallelTable[{

(* 1 Hintergrundpanorama *)
ImageTransformation[pct1, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width1},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 2 Sphäre *)
ImageTransformation[pct2, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-3π/2, π/2-2π/width2},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 3 Scheibe Textur *)
ImageTransformation[pic3, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width3},
{si, sr+(sr-si)/height3}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 4 Scheibe Geometrie *)
ImageTransformation[pic4, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width4},
{si, sr}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],

(* 5 Hintergrundpanorama *)
ImageTransformation[pct3, ray17, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width5},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+vvs/vzoom+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 6 Sphäre *)
ImageTransformation[pct3, ray16, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{-π, π-2π/width5},
{-π/2, 3π/2}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+x+vvs/vzoom, -π/2+x+π/kernels/grain+vvs/vzoom} vzoom
},
Resampling->rsp, Padding->"Periodic"],
 
(* 7 Scheibe Textur komplett *)
ImageTransformation[pic7, ray01, {breite, Ceiling[hoehe/kernels/grain]},
DataRange->{
{0, 2π-2π/width5},
{si, sr+(sr-si)/height5}
},
PlotRange->{
{-π+hvs/hzoom, π+hvs/hzoom} hzoom,
{-π/2+vvs/vzoom+x, -π/2+vvs/vzoom+x+π/kernels/grain} vzoom
},
Resampling->rsp, Padding->"Periodic"]

}, {x, 0, π-π/kernels/grain, π/kernels/grain}];

image[num_] := ImageAssemble[Table[{img[[x, num]]}, {x, kernels grain, 1, -1}]];
fi[x_] := ColorNegate[x];

Grid[{Table[image[n], {n, 1, 7, 1}]}]

Quit[]










Output (in diesem Beispiel mit unbewegter Scheibe und ruhendem Beobachter, r=100, θ=70°, rk=3, ri=3, ra=7):



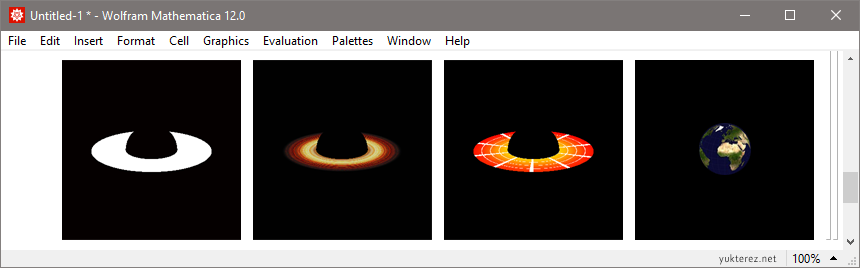
Aberration mit vr=vθ=0, vφ=0.95 (ArcSin[vφ]=71.8°) auf θ=70°; rk=3, ri=4, ra=7; 1. Zeile: r=40, r=30, 2. Zeile: r=20, r=10:



Vergleich der Perspektive eines Freifallers mit der eines ZAMO außerhalb und innerhalb eines SL mit Akkretionsscheibe:

Zusätzliche Rot/Blauverschiebung durch die Geschwindigkeit und Bewegungsrichtung des Beobachters (mittlerweile obsoloet, da bereits in die neuen Versionen des Raytracers eingebaut):

Code: Alles auswählen

pic=Import["http://yukterez.net/mw/gradient2.png"];                   (* Frequenzgradient *)

vr = -0.5;                                          (* radiale Geschwindigkeitskomponente *)
vφ = +0.5;                                        (* azimutale Geschwindigkeitskomponente *)
vθ = +0.5;                                           (* polare Geschwindigkeitskomponente *)

ς  = +1;                                                                         (* Lapse *)

width  = 120;                                                                 (* Bildhöhe *)
height = 60;                                                                (* Bildbreite *)

v  = +Sqrt[vr^2+vθ^2+vφ^2];
If[v>1, Print["Error: v > 1: v" -> v], Print["v" -> v]];

dΘ = +Limit[ArcCos[-vθ/Sqrt[vR^2+vθ^2+vφ^2]], vR->vr];
dθ = If[vr>0, -dΘ, +dΘ];
dΦ = +Limit[ArcTan[Abs[vφ]/vR], vR->vr];
dφ = If[vr!=0, -1, 1] If[vφ<0, +1, -1] If[NumericQ[dΦ], dΦ, π/2];
dψ = 0 If[vr<0, 0, π];

f[{φ_,θ_}] := {0, ς/(1-v Cos[θ-π/2]) Sqrt[1-v^2]};            (* winkelabhängige Frequenz *)

img = ImageTransformation[pic, f, {width, height},                     (* Frequenzbereich *)
DataRange->{{-1, 1}, {0, 2}},
PlotRange->{{-π, π}, {-π/2, π/2}},
Padding->"Fixed"];

xyz[{x_,y_}] := {Sin[y] Cos[x],Sin[y] Sin[x],Cos[y]};                  (* Rotationsmatrix *)
Xyz[{x_,y_,z_},dφ_] := {x Cos[dφ]-y Sin[dφ],x Sin[dφ]+y Cos[dφ],z};
xYz[{x_,y_,z_},dθ_] := {x Cos[dθ]+z Sin[dθ],y,z Cos[dθ]-x Sin[dθ]};
xyZ[{x_,y_,z_},dψ_] := {x,y Cos[dψ]-z Sin[dψ],y Sin[dψ]+z Cos[dψ]};
xy[{x_,y_,z_}] := {ArcTan[x,y],ArcCos[z]};

rm[img_,dφ_,dθ_,dψ_] := xy[xyZ[xYz[Xyz[xyz[img], dφ], dθ], dψ]];              (* Rotation *)
RM[{x_,y_}] := rm[{x,y}, dφ, dθ, dψ];

red = ImageTransformation[img, RM,               (* Output im 360°x180° Plattkartenformat *)
DataRange->{{-π, π}, {0, π}},
PlotRange->{{-π, π}, {0, π}},
Padding->"Periodic"]










[Yukterez]

◩ Code Version A, rechtwinkelige Leinwand


Konstruktion der Sichtebene:

 
Die türkis gestrichelte Kurve zeigt was man dort wo man im flachen Raum die linke untere Ecke des Bildes sehen würde sieht (dadurch erscheint das gravitationsgelinste Bild größer als das unverzerrte). Vorläufige Testbilder mit M=Q=a=0 (Vakuum), a=Q=0 (Schwarzschild) und a=M (extremal Kerr), erstellt mit auf 500 begrenzten Integrationsschritten pro Pixel; Perspektive: äquatorial.

Das schwarze Loch befindet sich relativ zum Betrachter in einer kartesischen Entfernung von 20GM/c². Der Mittelpunkt des betrachteten Bilds das sich auf einer rigiden stationären Leinwand die rechtwinkelig zur Sichtachse des Beobachters steht befindet ist ebensoweit vom schwarzen Loch, und damit doppelt so weit vom Betrachter entfernt. Die projizierte Sichtebene beträgt 60x60(GM/c²)²; alle Lichtstrahlen die von wo anders als der Leinwand kämen werden grau dargestellt.

Die projizierte Sichtebene in der Entfernung des schwarzen Lochs ist wegen der halben Entfernung damit 30x30(GM/c²)². Der Durchmesser des Schattens des schwarzen Lochs beträgt ca. 1/3 und damit 10GM/c², was einem Radius von ca. 5GM/c² entspricht (zum Vergleich siehe die semianalytische Konturlösung auf gravitylense.yukterez.net):



In der unteren (also der mittleren) Reihe befindet der Beobachter sich 100 Mal weiter vom schwarzen Loch entfernt, in einem kartesischen Abstand von 2000GM/c². Die Leinwand befindet sich ebensoweit in die andere Richtung vom SL entfernt; durch den nun spitzeren Sichtwinkel und den kleineren Impact Parameter der Photonen ergibt sich jetzt eine sehr viel stärkere Verzerrung.

Ohne schwarzes Loch im Vordergrund würde man innerhalb des Sichtwinkels im Zoom das gleiche Bild wie oben links, bzw. unten links in der Mitte (die 4 bekannten Kästchen) sehen; das heißt die höhere Entfernung wird durch höheren Zoom kompensiert, so dass das schwarze Loch den gleichen Winkeldurchmesser hat wie im oberen Beispiel (die Kamera ist immer noch auf das nun 100 mal weiter entfernte und rot umrahmte Quadrat von 30GM/c² Kantenlänge fokussiert):

Der graue Bereich symbolisiert wieder den Bereich wo keine Photonen von der Leinwand, aber theoretisch welche von seitwärts derselben beim Betrachter ankommen können (siehe nächstes Kapitel). Im komplett schwarzen Bereich würden weder Photonen von der Leinwand noch von sonst irgendwo im Raum das Auge des Betrachters treffen.

Die gerade Leinwand wird auf den y,z-Achsen bis in die Unendlichkeit fortgesetzt und das Bild wie unten links auf dieselbe gekachelt, da man ansonsten nicht viel sehen würde weil das Bild in der Entfernung vom Schatten des schwarzen Lochs verdeckt werden würde. Unterste Reihe: nackte Singularitäten mit Q=2M, a²+Q²=2M² und a=2M, Abstände wie in der mittleren Reihe:

[Yukterez]

◐ Code Version B, Panorama


Konstruktion der Sichtebene:



Also im Prinzip wie oben, aber mit Mapping des gesamten Umfelds um auch Licht das von außerhalb der Leinwand ins Sichtfeld der Kamera gebogen wird einzufangen. Fokus auf einen kleinen Bereich simuliert eine Lochkamera, während eine Plot-Range von φ=-π..π und θ=-π/2..π/2 ein 360° Kugelpanorama ergibt. Das gesamte Kugelsphärenpanorama wird dann ins Plattkartenformat exportiert und kann danach in jedes beliebige andere Format transformiert oder anderweitig projiziert werden. In den folgenden Beispielen wird der Beobachter auf r=50GM/c² platziert und das Himmelszelt auf R=1000GM/c² aufgespannt.



Sphärischer Hintergund: Milchstraßenpanorama (360°-Aufnahme im Plattkartenformat, Fotocredit ESO/José Francisco). Zoom auf den Bereich vor dem das schwarze Loch platziert wird; ungelinste Ansicht ohne das schwarze Loch im Vordergrund, FOV=120°×60°:





Schwarzschild: M=1, a=0, ℧=0 → ℳ=1 - einfaches schwarzes Loch, Beobachter auf r=50GM/c², θ=egal (kugelsymmetrisch), FOV=120°×60°:





Reissner-Nordström: M=1, a=0, ℧=1 → ℳ=½ - geladenes SL, Beobachter auf r=50GM/c², θ=egal (kugelsymmetrisch), FOV=120°×60°:





Kerr-Newman: M=1, a=√½, ℧=√½ → ℳ=√(3/8) - Geladen und rotierend, Beobachter auf r=50GM/c², θ=90° (äquatorial), FOV=120°×60°:





Kerr-Newman: M=1, a=√½, ℧=√½ → ℳ=√(3/8) - Geladen und rotierend, Beobachter auf r=50GM/c², θ=45° (schräg), FOV=120°×60°:





Kerr-Newman: M=1, a=√½, ℧=√½ → ℳ=√(3/8) - Geladen und rotierend, Beobachter auf r=50GM/c², θ=1° (polar), FOV=120°×60°:





Kerr: M=1, a=1, ℧=0 → ℳ=√½ - Beobachter auf r=50GM/c², θ=90° (äquatorial), FOV=120°×60°:





Kerr: M=1, a=1, ℧=0 → ℳ=√½ - Beobachter auf r=50GM/c², θ=45° (schräg), FOV=120°×60°:





Kerr: M=1, a=1, ℧=0 → ℳ=√½ - Beobachter auf r=50GM/c², θ=1° (polare Ausrichtung, Rotation gegen den Uhrzeigersinn), FOV=120°×60°:





Einheiten: G=M=c=k=1. M=Massenäquivalent der Gesamtenergie, ℳ=irreduzible Masse, a=Spinparameter, ℧=Ladung G=Gravitationskonstante, k=Coulombkonstante, c=Lichtgeschwindigkeit. Die Gesamtenergie Mc² des schwarzen Lochs ist in allen obigen Szenarien gleich, aber unterschiedlich auf irreduzible Masse, Rotationsenergie und elektromagnetische Feldenergie aufgeteilt.

[Yukterez]

Rohmaterial: Panoramaphoto geschossen von Masato OHTA (heiwa4126), Source: Commons, Ort: Tokyo. Assumptions: alles im Panorama ist sehr viel weiter vom Beobachter entfernt als das schwarze Loch. Hier wird nur der Gravitationslinseneffekt gezeigt, nicht aber die Zerstörung die ein SL in so einem Szenario anrichten würde.


SL: M=1, a=1, ℧=0. FOV=360°×180°, ungelinstes Panorama:



Zoom auf die Stelle an der das schwarze Loch platziert wird, Ф=0°, θ=0°, FOV=103.2°×61.4°:



Das schwarze Loch ist r=50GM/c² vom Beobachter entfernt. Position, Fokus und Zoom auf Ф=0°, θ=0°, FOV=103.2°×61.4°:



Entfernung vom SL: 20GM/c². Position, Fokus und Zoom auf Ф=0°, θ=0°, FOV=103.2°×61.4°:





Blick in die entgegengesetzte Richtung, FOV=360°×180°:



Zoom auf die Stelle an der das schwarze Loch platziert wird, Ф=0°, θ=180°, FOV=103.2°×61.4°:



Entfernung vom SL: 50GM/c². Position, Fokus und Zoom auf Ф=180°, θ=0°, FOV=103.2°×61.4°:



Entfernung vom SL: 20GM/c². Position, Fokus und Zoom auf Ф=180°, θ=0°, FOV=103.2°×61.4°:





Hier wird das schwarze Loch auf halber Höhe über der Skyline platziert; Ansicht ohne SL, FOV=103.2°×61.4°:



Entfernung vom SL: 50GM/c². Position, Fokus und Zoom auf Ф=180°, θ=-45°, FOV=103.2°×61.4°:



Entfernung vom SL: 20GM/c². Position, Fokus und Zoom auf Ф=180°, θ=-45°, FOV=103.2°×61.4°:

[Yukterez]

Die folgenden überextremen Lösungen beschreiben keine schwarzen Löcher, und kommen in der Natur vermutlich nicht so vor. Da sie aber dennoch von theoretischem Interesse sind bekommen sie ebenfalls eine Gallerie. Wie im oberen Beitrag mit den schwarzen Löchern ist auch hier die Gesamtenergie Mc² der nackten Singularitäten in allen Beispielen gleich, aber verschieden aufgeteilt.

Standbilder (a²+℧²=2², zum Vergrößern auf die Bilder klicken)

relativistic raytracing of the shadow and the gravitational lensing of naked singularities
Reissner-Nordström: M=1, a=0, ℧=2 → ℳ=½+i√¾ - nackte Singularität. Beobachter: r=50GM/c², θ=egal (kugelsymmetrisch), FOV=120°×60°:





Kerr-Newman: M=1, a=√2, ℧=√2 → ℳ=∜(3/16)·(1+i) - nackte Singularität. Beobachter: r=50GM/c², θ=90° (äquatorial), FOV=120°×60°:





Kerr-Newman: M=1, a=√2, ℧=√2 → ℳ=∜(3/16)·(1+i) - nackte Singularität. Beobachter: r=50GM/c², θ=45° (schräg), FOV=120°×60°:





Kerr-Newman: M=1, a=√2, ℧=√2 → ℳ=∜(3/16)·(1+i) - nackte Singularität. Beobachter: r=50GM/c², θ=1° (polar), FOV=120°×60°:





Kerr: M=1, a=2, ℧=0 → ℳ=√¾+i/2 - nackte Singularität. Beobachter: r=50GM/c², θ=90° (äquatorial), FOV=120°×60°:





Kerr: M=1, a=2, ℧=0 → ℳ=√¾+i/2 - nackte Singularität. Beobachter: r=50GM/c², θ=45° (schräg), FOV=120°×60°:





Kerr: M=1, a=2, ℧=0 → ℳ=√¾+i/2 - nackte Singularität. Beobachter: r=50GM/c², θ=1° (polar), FOV=120°×60°:

[Yukterez]

a=+1, Beobachter auf r=50, ri=1.01, ra=7, Scheibentextur: scheibe.png, geometrische Verzerrung:



Selbe Tabelle wie oben mit Falschfarbcodierung, weiße Linien markieren den Übergang zwischen Rot- und Blauverschiebung:



Proberechnung: Project Kerr 599 (links) vs Yukterez (rechts), a=-0.6, θ=86°, ri=4, ra=10, Scheibentextur: akkr.png mit Transparenz und Glow



Erklärung, andere Beispiele und Vergleiche: siehe hier, hier & hier.

[Yukterez]

Reissner Nordström, schwarzes Loch, Blickwinkel: θ=85° (FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei prograder relativistischer Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Reissner Nordström, schwarzes Loch, Blickwinkel: θ=45° (FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Kerr Newman, schwarzes Loch, Blickwinkel: θ=85° (isco=1.313818, FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Kerr Newman, schwarzes Loch, Blickwinkel: θ=45° (FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Nackte Singularität, θ=85° (FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Nackte Singularität, θ=45° (FOV=30°×24°):



radiale weiße Linien für konstante φ:



Retardierung bei Kreisgeschwindigkeit der Scheibe, Synchronsierung bei t=-r/c:



Rot- und Blauverschiebung:



Overlay mit nacktem Schatten:



Unverzerrte Ansicht:

[Yukterez]

Separate Ansicht der Lichtechos aus dem vorherigen Beispiel (a=1, ℧=0.3, θ=45°, r=50, ri=1, ra=10, FOV=30°×24°):



Zoom auf das Fenster in den negativen Raum, auch Antiwelt genannt (blau markiert). FOV=10°×8°:



Der Bereich zwischen der nackten Ringsingularität (r=0, R=a=1) und dem Innenrand der Akkretionsscheibe (r=1, R=√2) ist gravitativ abstoßend, weswegen dort auch keine Orbits (weder stabil noch unstabil) möglich sind. Wie es hinter dem Fenster zwischen dem Ring aussieht und ob die Welt dahinter leer und dunkel oder bevölkert und hell ist ist unbekannt und bis auf weiteres der Phantasie des Betrachters überlassen, weswegen der Bereich am Bild ausgespart ist. Für mehr zum Thema siehe auch hier und hier.

[Yukterez]

Parameter wie beim Interstellar SL "Gargantua", jedoch mit gleichmäßiger und transparenter Scheibentextur:



Photoshop Aktionen für die Post Production: Download

[Yukterez]

Erde mit Ring, Beobachter ruhend beim 6.667fachen Erdradius:



Mit vφ=0.95 auf r=6.667rk, θ=70° vorbeifliegender Beobachter (Aberrationswinkel Δφ=ArcSin[vφ]=71.8°):



Ruhender Beobachter beim 3.333fachen Erdradius:



Auf r=3.333rk, θ=70° vorbeifliegender Beobachter (vφ=0.95):



Siehe auch der Ball ist rund und rollende Räder.

[Yukterez]

Mathematischer Anhang (im Aufbau):

1) Geschwindigkeitskomponenten der beim Betrachter eintreffenden Strahlen


Das schwarze Loch befindet sich im lokalen Koordinatensystem des Beobachters auf {x,z}={0,0}. Der {x,y,z}-Vektor eines geradewegs von vorne kommenden Photons ist daher



Rotation entlang der x-Achse:



Rotation entlang der z-Achse:



Normierter Geschwindigkeitsvektor der eintreffenden Strahlen im euklidschen Referenzsystem:



Aberration bei lokaler (relativ zum ZAMO) Beobachtergeschwindigkeit {ur,uθ,uФ}:



mit den Komponenten



Radiale Komponente:



Polare Komponente:



Azimutale Komponente:



Das sind die Endbedingungen der im Auge des Betrachters auf der {α,β}-Sichtebene eintreffenden Strahlen. Diese werden hernach rückwärts integriert bis sie die Ebene des Interesses, in dem Fall ein auf R>>r aufgespanntes Kugelpanorama, treffen.


2) Bewegungsgleichung der Photonen und Partikel:


Erste Ableitung:



Zweite Ableitung:



mit den Christoffelsymbolen



Für die aufsummierten Terme in expliziter Form siehe den Faden über die Kerr Newman Metrik.


3) Bildtransformation


Nun wird numerisch nach der Eigenzeit bzw. dem affinen Parameter bei dem das Photon in der Region des Interesses (in dem Fall auf der auf R aufgespannten Kugelschale) war gesolved:



Die für τ berechneten {Ф,θ} Koordinaten des Lichtstrahls werden dann vom Rohmaterial im Plattkartenformat auf die lokale Sichtebene gemappt:




4) Akkretionsscheibe


Mapping des Rohmaterials auf die {r,Ф} statt auf die {Ф,θ} Ebene, Versatz um ΔФ=t·ω oder ΔФ=t/ṫ·uФ (Koordinatenzeit mal Framedragging Winkelgeschwindigkeit oder Kreisorbitwinkelgeschwindigkeit)


5) Frequenzverschiebung




wobei vdisc die lokale Kreisbahngeschwindigkeit der Scheibe ist, und vφ die axiale lokale Geschwindigkeitskomponente des Photons wenn es die Scheibenebene kreuzt. ς ist die gravitative Zeitdilatation des ZAMO auf der Position des Beobachters, und ṫ die gesamte Zeitdilatation dt/dτ auf der kreisenden Scheibe. Für einen lokal bewegten Beobachter kommt noch die kinematische Rot/Blauverschiebung hinzu.


6) Horizontoberfläche


Wie 3), nur auf r+ statt auf R und mit ΔФ

images, animations and codes by Simon Tyran, Vienna (Yukterez) - reuse permitted under the Creative Commons License CC BY-SA 4.0