Beitragvon Zarathustra » So 29. Nov 2015, 20:47
Ein Objekt legt in einem dreidimensionalen Raum die Strecke (Abstand -Distanz-Länge,) zwischen A und B (x) mit einer bestimmten Geschwindigkeit (v) in einer bestimmten Zeit(t) zurück.
Die Formel für den Abstand zwischen A und B (x) lautet:
x=vt
Was die Messung des (dreier) Abstandes im dreidimensiolen Raum betrifft, sind sich alle einig weil dieser Abstand (x) zwischen A und B bekannt (existent) ist und mit einem Lineal gemessen werden kann.
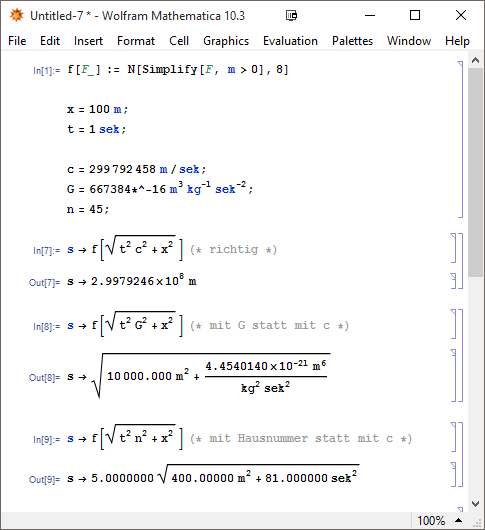
Die Formel für den Vierer-Abstand zwischen A und B (s) lautet:
s=wurzel c²t²-v²t²
In dieser (Lorentz) Formel taucht eine konstante (c) auf, die natürlich nicht geändert werden darf, sonst bekommt man unendlich viele rechnerische Ergebnisse für den Vierer- Abstand (s), die nicht alle richtig sein können, sondern nur eine, die nach Lorenz nur dann richtig ist wenn für c die Lichtgeschwindigkeit eingesetzt wird, den wir s1 nennen und nicht jede belieige andere Geschwindigkeiten, (z.B.c1,c2, c3, c4,..) die wählbar wären und andere Werte (s2,s3,s4,..) für den Vierer-Abstand ergeben würden.
Die Frage lautet:
Welcher Abstand in reale Welt gemessen werden soll, um nachzuweisen, dass nur s1 (Lorentz Vierer-Abstand) den richtigen Abstand zwischen A und B in einem vierdimensionalen Raum(zeit) darstellt und nicht s2, oder s3 usw..
Von wo bis wo?
Völlig verwirrtes Äffchen, damit Du deine Geduld nicht verlierst, habe ich es noch mal ohne Zahlen erklärt.



 ,
,