Transformation in ein bewegtes System
Verfasst: Di 23. Feb 2016, 00:03
Code: Alles auswählen
(*SYSTEM BEOBACHTER*)
L = {Line[{{-3, 0}, {3, 0}}]};
R = {PointSize[Large], Red, Point[{{0, 0}}]};
B = {PointSize[Large], Blue, Point[{{-2, 0}, {2, 0}}]};
o = {PointSize[Large], Orange, Point[{{0, 0}}]};
tmin = -7; tmax = 15; v = 0.8 c; c = 1; \[Gamma] = 1/Sqrt[1 - v^2];
plotB = Manipulate[
Graphics[ {Piecewise[{{{L, R,
B, {PointSize[Large], Brown, Point[{{-v t + 2, 0}}]}},
t < 0}, {{L, R,
B, {PointSize[Large], Green,
Point[{{-v t + 2, 0}}]}, {PointSize[Large], Yellow,
Point[{{-c t + 2, 0}}]}},
t <= 2 && t >= 0}, {{L, o,
B, {PointSize[Large], Green, Point[{{-v t + 2, 0}}]}},
t > 2 && t < 5}, {{L, o,
B, {PointSize[Large], Yellow,
Point[{{+c t - 7, 0}}]}, {PointSize[Large], Brown,
Point[{{-v t + 2, 0}}]}},
t >= 5 && t <= 25/4}, {{L, o,
B, {PointSize[Large], Yellow, Point[{{+c t - 7, 0}}]}},
t > 25/4 && t <= 7}, {{L, R, B}, t > 7}}]},
PlotRange -> {{-3, 3}, {-1, 1}}, ImageSize -> 500, Frame -> True,
FrameTicks -> {{None, None}, {All, None}}], {{t, tmin \[Gamma],
"t"}, tmin \[Gamma], tmax \[Gamma]}]
(*SYSTEM LAMPE*)
plotL = Manipulate[
Show[Graphics[{Piecewise[{{{{Line[{{-5, 0}, {7, 0}}]}, {PointSize[
Large], Red, Point[{{-6/5 + v t, 0}}]}, {PointSize[Large],
Blue, Point[{{-12/5 + v t, 0}, {0 + v t, 0}}]}, {PointSize[
Large], Brown, Point[{{0, 0}}]}},
t < 0}, {{{Line[{{-5, 0}, {7, 0}}]}, {PointSize[Large], Red,
Point[{{-6/5 + v t, 0}}]}, {PointSize[Large], Blue,
Point[{{-12/5 + v t, 0}, {0 + v t, 0}}]}, {PointSize[Large],
Green, Point[{{0, 0}}]}, {PointSize[Large], Yellow,
Point[{{-c t, 0}}]}},
t >= 0 &&
t <= 2/3}, {{{Line[{{-5, 0}, {7, 0}}]}, {PointSize[Large],
Orange, Point[{{-6/5 + v t, 0}}]}, {PointSize[Large], Blue,
Point[{{-12/5 + v t, 0}, {0 + v t, 0}}]}, {PointSize[Large],
Green, Point[{{0, 0}}]}},
t > 2/3 &&
t <= 3}, {{{Line[{{-5, 0}, {7, 0}}]}, {PointSize[Large],
Orange, Point[{{-6/5 + v t, 0}}]}, {PointSize[Large], Blue,
Point[{{-12/5 + v t, 0}, {0 + v t, 0}}]}, {PointSize[Large],
Brown, Point[{{0, 0}}]}, {PointSize[Large], Yellow,
Point[{{c t - 3, 0}}]}},
t > 3 &&
t <= 9}, {{{Line[{{-5, 0}, {7, 0}}]}, {PointSize[Large], Red,
Point[{{-6/5 + v t, 0}}]}, {PointSize[Large], Blue,
Point[{{-12/5 + v t, 0}, {0 + v t, 0}}]}, {PointSize[Large],
Brown, Point[{{0, 0}}]}}, t > 9}}]},
PlotRange -> {{-3, 7}, {-5/3, 5/3}}, ImageSize -> 500,
Frame -> True, FrameTicks -> {{None, None}, {All, None}}]], {{t,
tmin, "\[Tau]"}, tmin, tmax}]
(*SLIDE*)
tB = Manipulate[
Evaluate[N[t]], {{t, tmin \[Gamma], "t"}, tmin \[Gamma],
tmax \[Gamma]}];
tL = Manipulate[Evaluate[N[t]], {{t, tmin, "\[Tau]"}, tmin, tmax}]; 
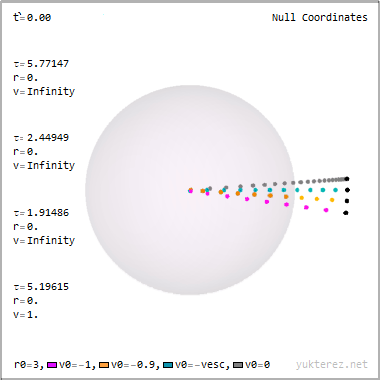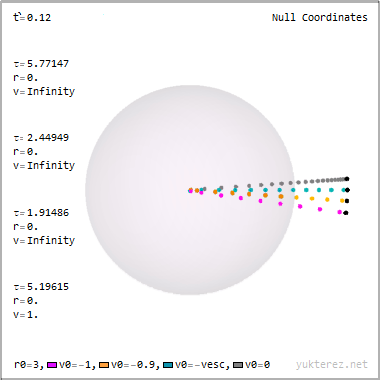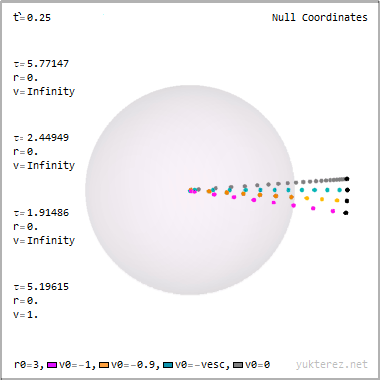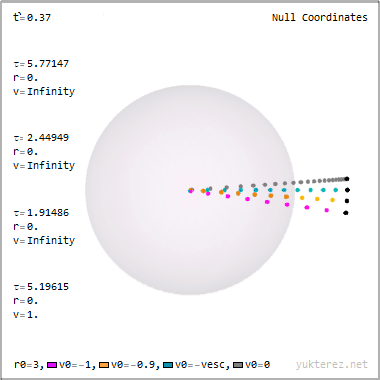
Im System des Beobachters, der auf dem Koordinatenursprung steht, bewegt sich eine Lampe mit 0.8 c auf ihn zu und beginnt in einer Entfernung von 2 Ls für 5 sek zu leuchten (im Lampensystem für 3 sek).
Gesucht ist nun die Lebensdauer (zeitlicher Abstand Emission zu Arbsorption) des ersten, mittleren und letzten Photons sowohl im System des Beobachters als auch im System der Lampe.
- Beobachtersystem:
 Da das erste Photon in 2 Ls Entfernung emittiert wird, beträgt die Lebensdauer des ersten Photons logischerweise 2 sek.
Da das erste Photon in 2 Ls Entfernung emittiert wird, beträgt die Lebensdauer des ersten Photons logischerweise 2 sek. Weil das letzte Photon wie im Link vorgerechnet in -2 Ls Abstand gesendet wird, ist dessen Lebensdauer identisch mit der des Ersten, also 2 sek.
Weil das letzte Photon wie im Link vorgerechnet in -2 Ls Abstand gesendet wird, ist dessen Lebensdauer identisch mit der des Ersten, also 2 sek.
- Lampensystem:
 Aufgrund der Längenkontraktion bei 0.8 c sind die 2 Ls Abstand zum Empfänger auf 3/5 ihrer Ruhelänge kontrahiert auf 6/5 Ls = 1.2 Ls.
Aufgrund der Längenkontraktion bei 0.8 c sind die 2 Ls Abstand zum Empfänger auf 3/5 ihrer Ruhelänge kontrahiert auf 6/5 Ls = 1.2 Ls.
Ebenso ist aus Sicht der Lampe der Beobachter der Bewegte; er bewegt sich also mit 0.8 c auf die Lampe zu.
Währenddessen fährt das erste Photon mit c relativ zur Lampe und damit mit 1.8 c relativ zum Empfänger voran.
Die relativistische Geschwindigkeitsaddition wird hier entgegen der landläufigen Meinung nicht angewandt.
Die Lebensdauer des ersten Photons beträgt damit (1.2 Ls)/(1.8 Ls/sek) = 2/3 sek = 0.'6 sek. Das Letzte Photon wird im selben Abstand, der auf die selben 1.2 Ls kontrahiert ist, ausgesendet.
Das Letzte Photon wird im selben Abstand, der auf die selben 1.2 Ls kontrahiert ist, ausgesendet.
Währenddessen bewegt sich der Empfänger mit 0.8 c von der Lampe weg, und das Photon mit 1 c.
Die Relativgeschwindigkeit zwischen Photon und Empfänger ist daher aus der Sicht der Lampe 0.2 c.
Die Lebensdauer des letzten Photons ist folgerichtig (1.2 Ls)/(0.2 Ls/sek) = 6 sek.
- Probe:
 (2/3+6)/4 = 5/3 = γ-Faktor 1/√(1-v²/c²)
(2/3+6)/4 = 5/3 = γ-Faktor 1/√(1-v²/c²)