Schwarzschild De Sitter Metrik (SSdS)
Verfasst: Di 29. Dez 2015, 21:08

 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  English version: click here
English version: click here
Um die Gravitation einer dominanten Masse im expandierenden Universum zu untersuchen bietet sich die Schwarzschild De Sitter Metrik an:

Die kritische Masse bei der der Horizont des schwarzen Lochs mit dem kosmischen Ereignishorizont zusammenfällt (Nariai Limit) liegt bei

wobei für die Radien der Horizonte
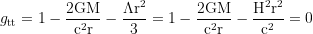
gesetzt und nach r aufgelöst wird.

Die Grenzmasse eines schwarzen Lochs in einem De Sitter Kosmos mit unserer kosmologischen Konstante (Λ≈1e-52/m²) wäre ≈4.3e52kg:


Die kritische Masse bei der der Horizont des schwarzen Lochs mit dem kosmischen Ereignishorizont zusammenfällt (Nariai Limit) liegt bei

wobei für die Radien der Horizonte
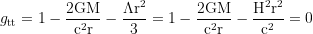
gesetzt und nach r aufgelöst wird.

Die Grenzmasse eines schwarzen Lochs in einem De Sitter Kosmos mit unserer kosmologischen Konstante (Λ≈1e-52/m²) wäre ≈4.3e52kg:

x-Achse: M (in kg), y-Achse: r (in Mrd. Lj.); grün/blau: Horizontradien (kosmischer Ereignishorizont und EH des SL), rot: Schwarzschildradius rs

Die Anziehungskraft einer Galaxie wie der unseren wird in einer Entfernung von ungefähr 1 Megaparsec durch die Expansion des Universums ausgeglichen, so dass ein Testpartikel der in diesem Abstand von der Galaxie ruht genauso stark von derselben angezogen wird wie er von der dunklen Energie von selbiger wegbeschleunigt wird.
Der physikalische Abstand eines Testpartikels von der dominanten Masse bleibt am Gleichgewichtsradius konstant. Wenn die Masse relativ zur Hintergrundstrahlung ruht, also mit dem Hubbleflow fließt, kann unser Testpartikel nicht mehr ebenfalls relativ zur Hintergrundstrahlung ruhen, da er sich dazu von der Masse entfernen müsste.
Gleichgewichtsradius: die neutonische Orbitalgeschwindigkeit wird gleich der Vakuumrezessionsgeschwindigkeit gesetzt und nach r aufgelöst:





Herleitung: der krtitische Radius ab dem ein Testpartikel relativ zur dominanten Masse stationär bleibt ist mit

und der sich damit ergebenden radialen Viererbeschleunigungskomponente

die gleich 0 gesetzt und nach r aufgelöst wird bei

Mit der im De Sitter Universum geltenden Relation

landen wir bei der weiter oben über die Rezessionsgeschwindigkeit erhaltenen Lösung


Für die benötigte Kreisbahngeschwindigkeit um die dominante Masse wird
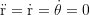
gesetzt und nach v aufgelöst:

was einer Winkelgeschwindigkeit von

entspricht, mit der auf M normierten dimensionslosen Länge und kosmologischen Konstante


Die lokale Fluchtgeschwindigkeit relativ zu einer stationären Boje ist mit

bzw. E=-pt=mc² und nach v aufgelöst

wobei das Minimum immer größer als 0 ist und beim oben erwähnten Gleichgewichtsradius liegt, dort beträgt es

Für einen Beobachter der mit der Fluchtgeschwindigkeit unterwegs ist gleicht sich die gravitative und die kinematische Zeitdilatation aus, so dass

Die Systeme dieser lokalen Beobachter bilden die Hyperfläche mit konstanten t in mitbewegten Koordinaten, während die lokalen Lineale und Uhren in den hier verwendeten Koordinaten stationär zum Zentrum sind.

Rezessionsgeschwindigkeit freifallender Partikel die nahe dem Gleichgewichtsradius entspringen (mit G=M=c=1 und Λ=0.01):

Der physikalische Abstand eines Testpartikels von der dominanten Masse bleibt am Gleichgewichtsradius konstant. Wenn die Masse relativ zur Hintergrundstrahlung ruht, also mit dem Hubbleflow fließt, kann unser Testpartikel nicht mehr ebenfalls relativ zur Hintergrundstrahlung ruhen, da er sich dazu von der Masse entfernen müsste.
Gleichgewichtsradius: die neutonische Orbitalgeschwindigkeit wird gleich der Vakuumrezessionsgeschwindigkeit gesetzt und nach r aufgelöst:





Herleitung: der krtitische Radius ab dem ein Testpartikel relativ zur dominanten Masse stationär bleibt ist mit

und der sich damit ergebenden radialen Viererbeschleunigungskomponente

die gleich 0 gesetzt und nach r aufgelöst wird bei

Mit der im De Sitter Universum geltenden Relation

landen wir bei der weiter oben über die Rezessionsgeschwindigkeit erhaltenen Lösung


Für die benötigte Kreisbahngeschwindigkeit um die dominante Masse wird
gesetzt und nach v aufgelöst:

was einer Winkelgeschwindigkeit von

entspricht, mit der auf M normierten dimensionslosen Länge und kosmologischen Konstante


Die lokale Fluchtgeschwindigkeit relativ zu einer stationären Boje ist mit

bzw. E=-pt=mc² und nach v aufgelöst

wobei das Minimum immer größer als 0 ist und beim oben erwähnten Gleichgewichtsradius liegt, dort beträgt es

Für einen Beobachter der mit der Fluchtgeschwindigkeit unterwegs ist gleicht sich die gravitative und die kinematische Zeitdilatation aus, so dass

Die Systeme dieser lokalen Beobachter bilden die Hyperfläche mit konstanten t in mitbewegten Koordinaten, während die lokalen Lineale und Uhren in den hier verwendeten Koordinaten stationär zum Zentrum sind.

Rezessionsgeschwindigkeit freifallender Partikel die nahe dem Gleichgewichtsradius entspringen (mit G=M=c=1 und Λ=0.01):

x-Achse: r (in GM/c²), y-Achse: v (in c); rot: Rezessionsgeschwindigkeit (relativ zu Fidos), grün: Geschwindigkeit eines E=mc² Partikels. Λ=c⁴/G²/M²/100=1/rs²/25
