Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  For the english version see here.
For the english version see here. 



Big Rip

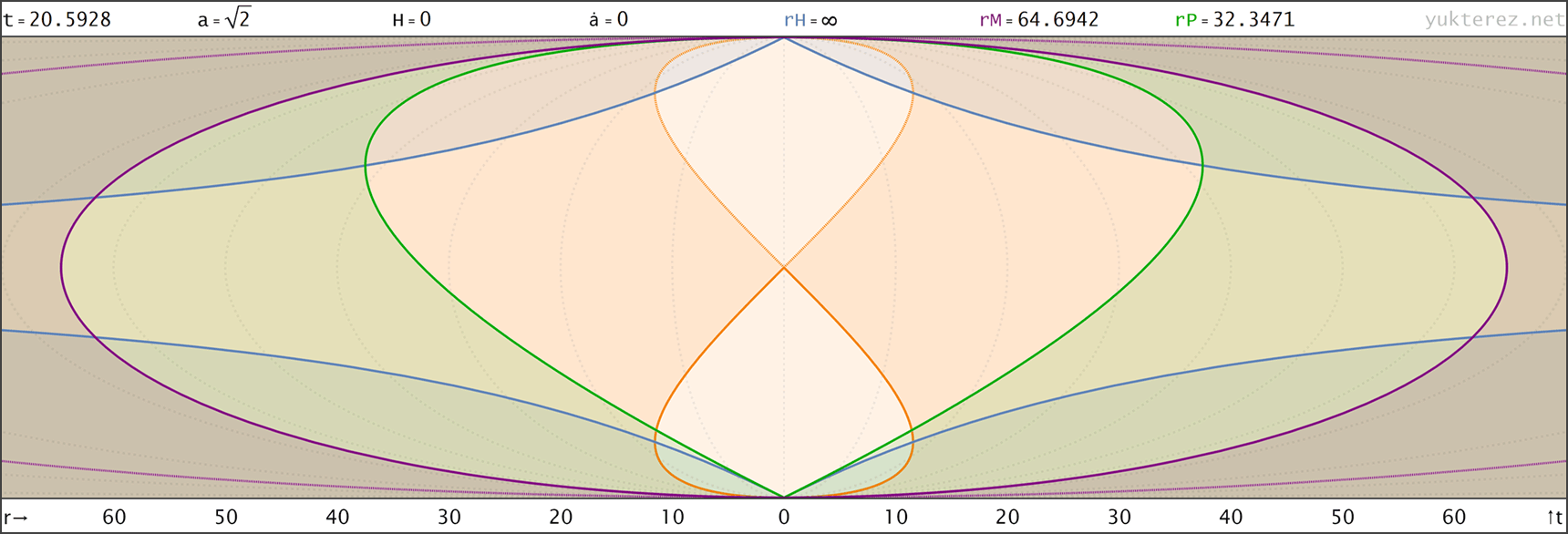
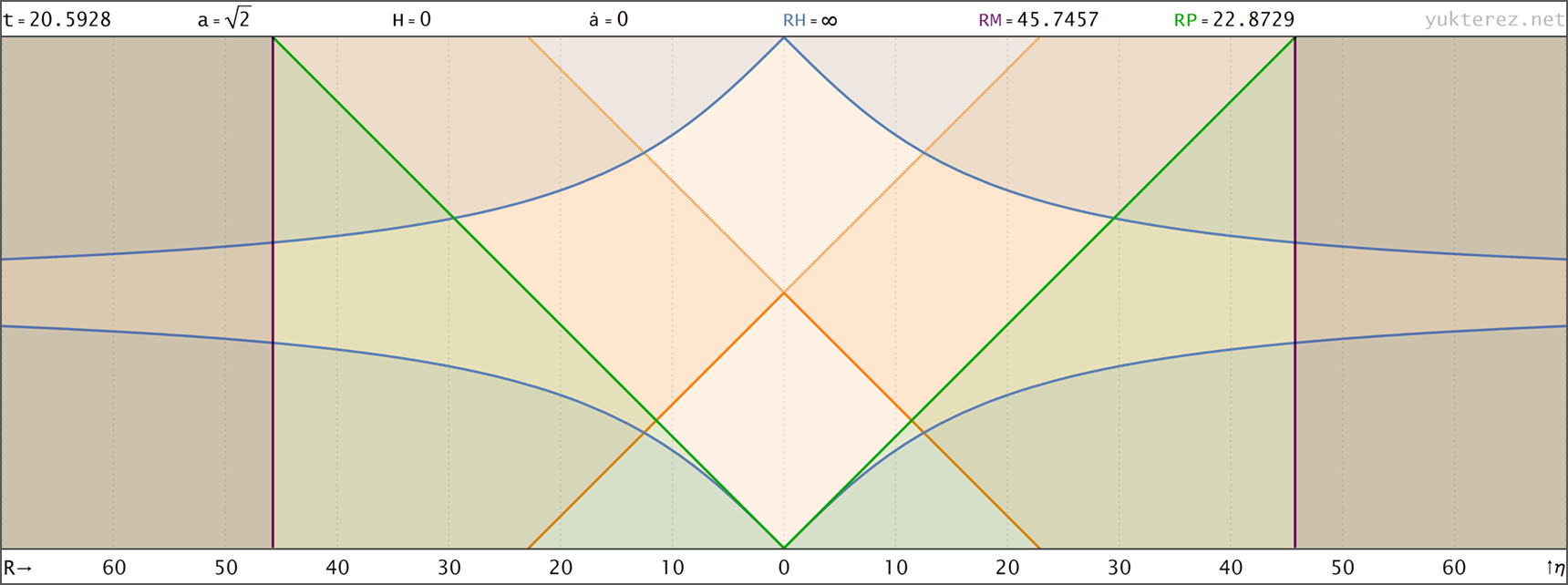
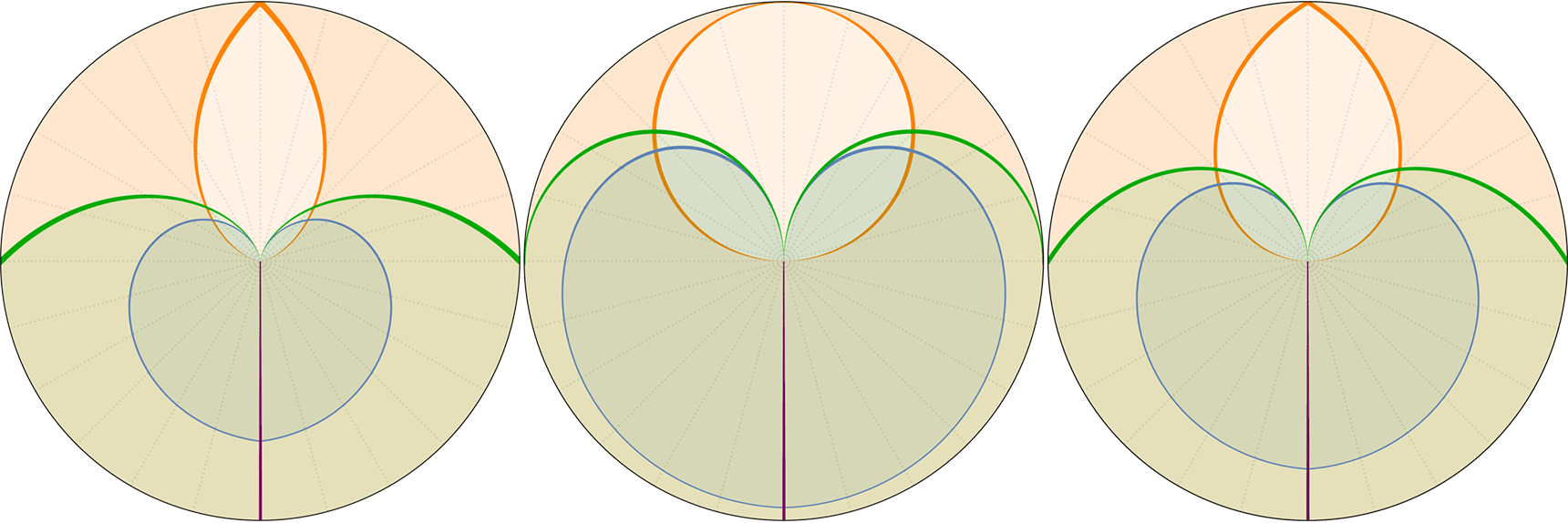
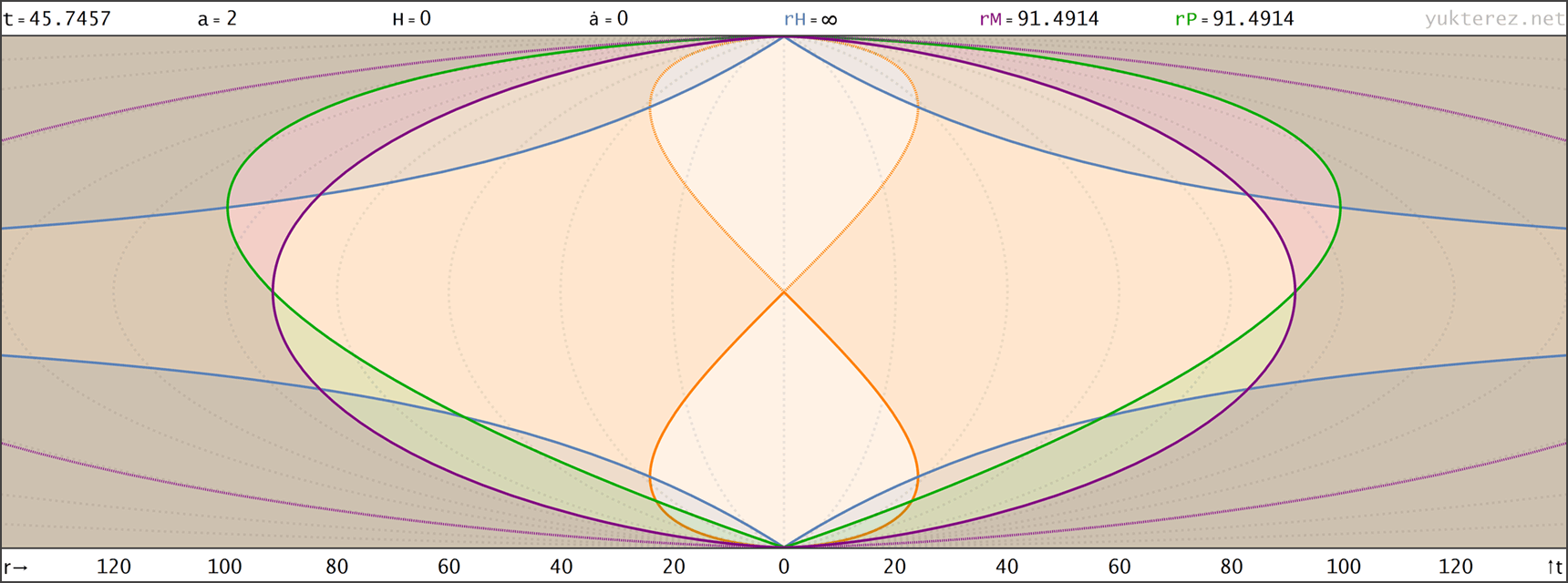
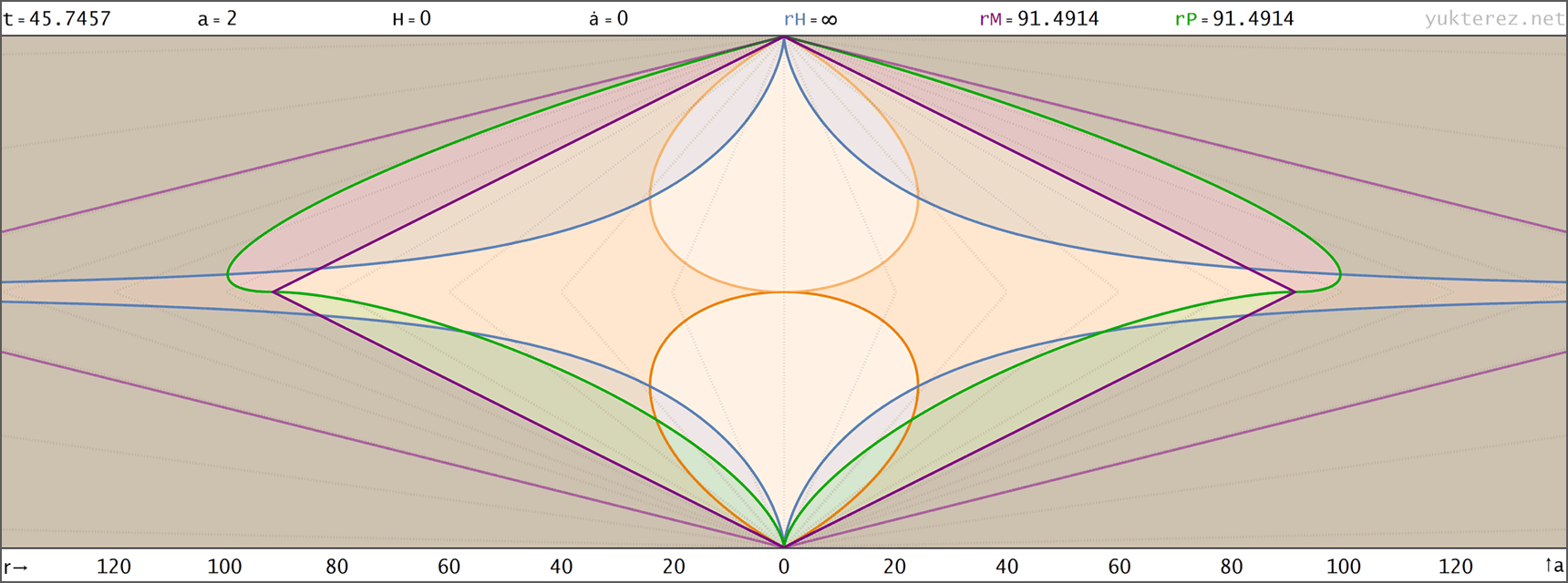
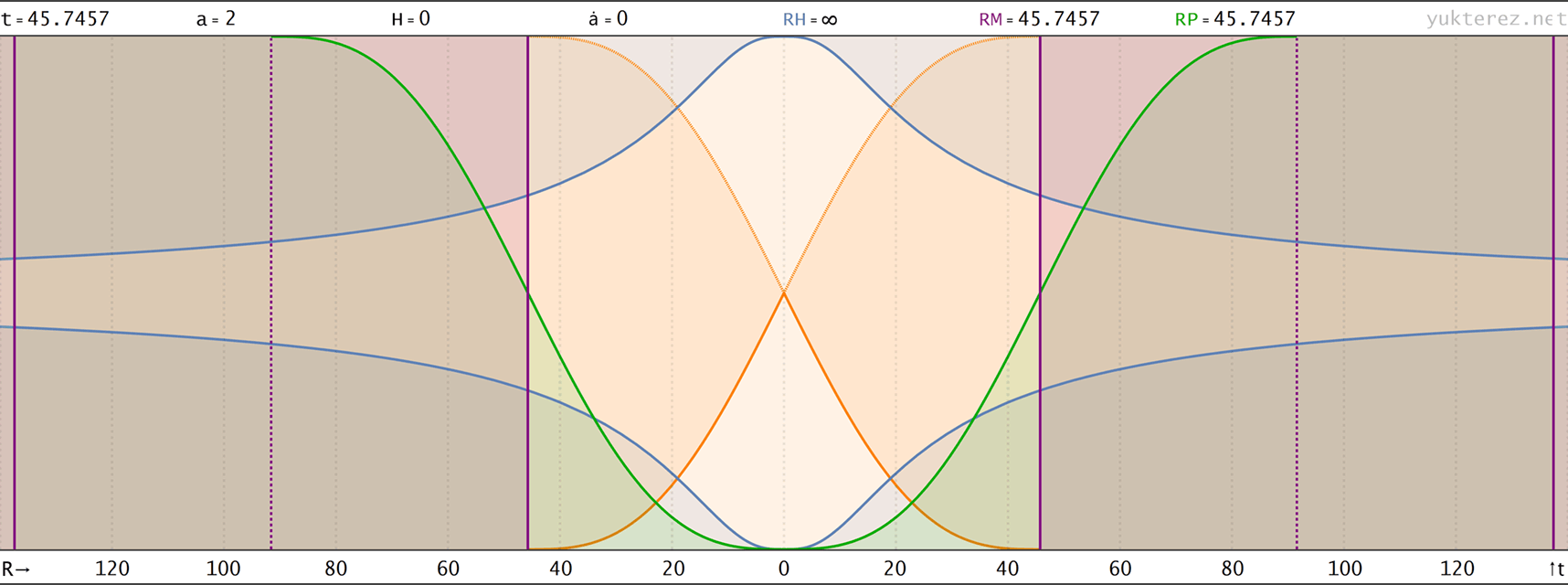
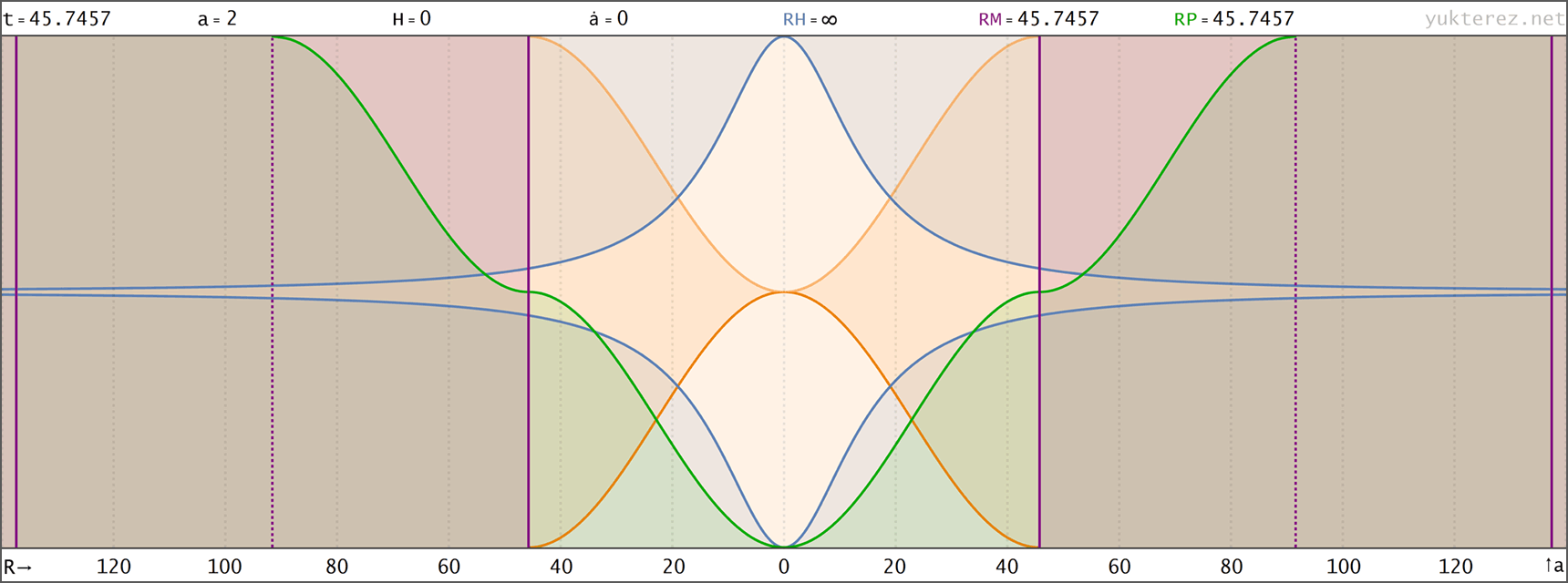
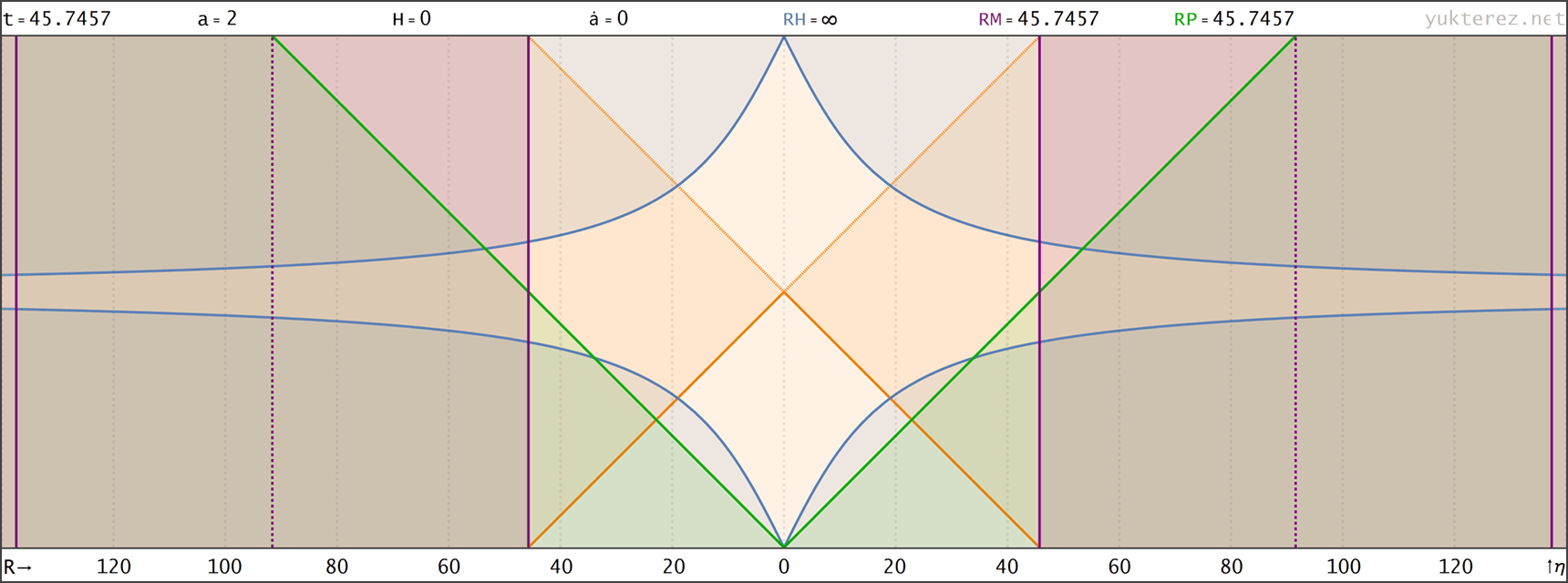
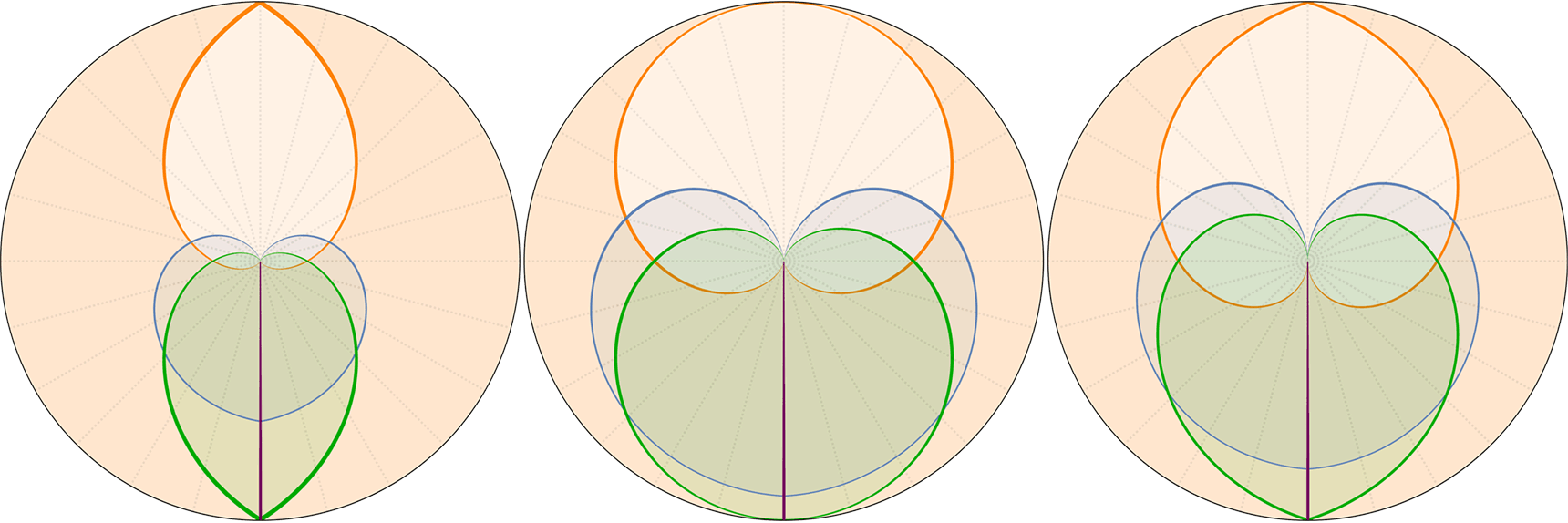
Evolution eines Big Rip Universums mit H=H0·√[Ωr/a⁴+Ωm/a³+Ωk/a²+ΩΛ·a] (Zustandsgleichung für Λ: w=-4/3); Anfangsbedingungen bei a=1: H0=67.15, Ωm=0.315, ΩΛ=0.685, Ωr=0, Ωk=0 → der Big Rip tritt bei t=48.836 Milliarden Jahren nach dem Urknall ein. Raumzeitdiagramme in Proper, Comoving & Conformal Koordinaten, der Lichtkegel entspringt bei a=1, t=14.4169 Gyr. rH: Hubble Radius (blau), rE: Ereignishorizont (violett), rP: Partikelhorizont (grün), orange Kurve: Lichtkegel, graue Kurven: mitbewegte Weltlinien, R=r/a:
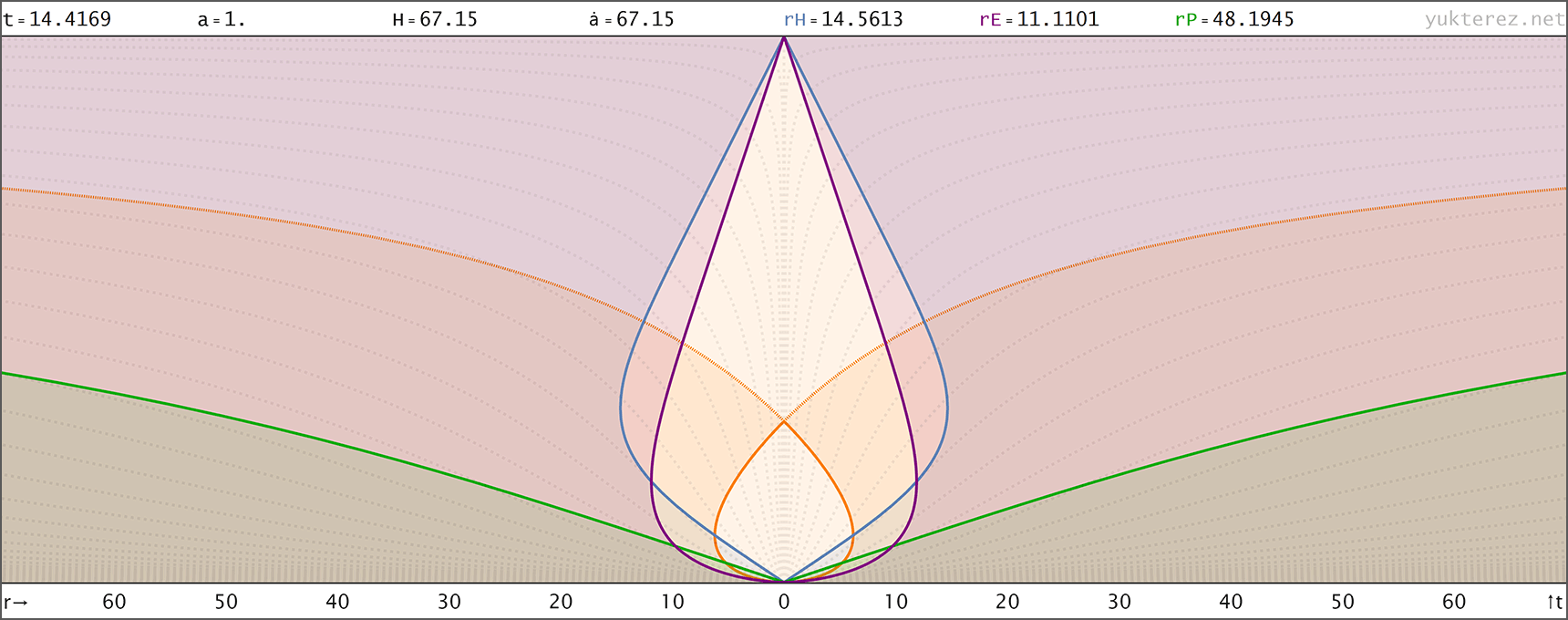
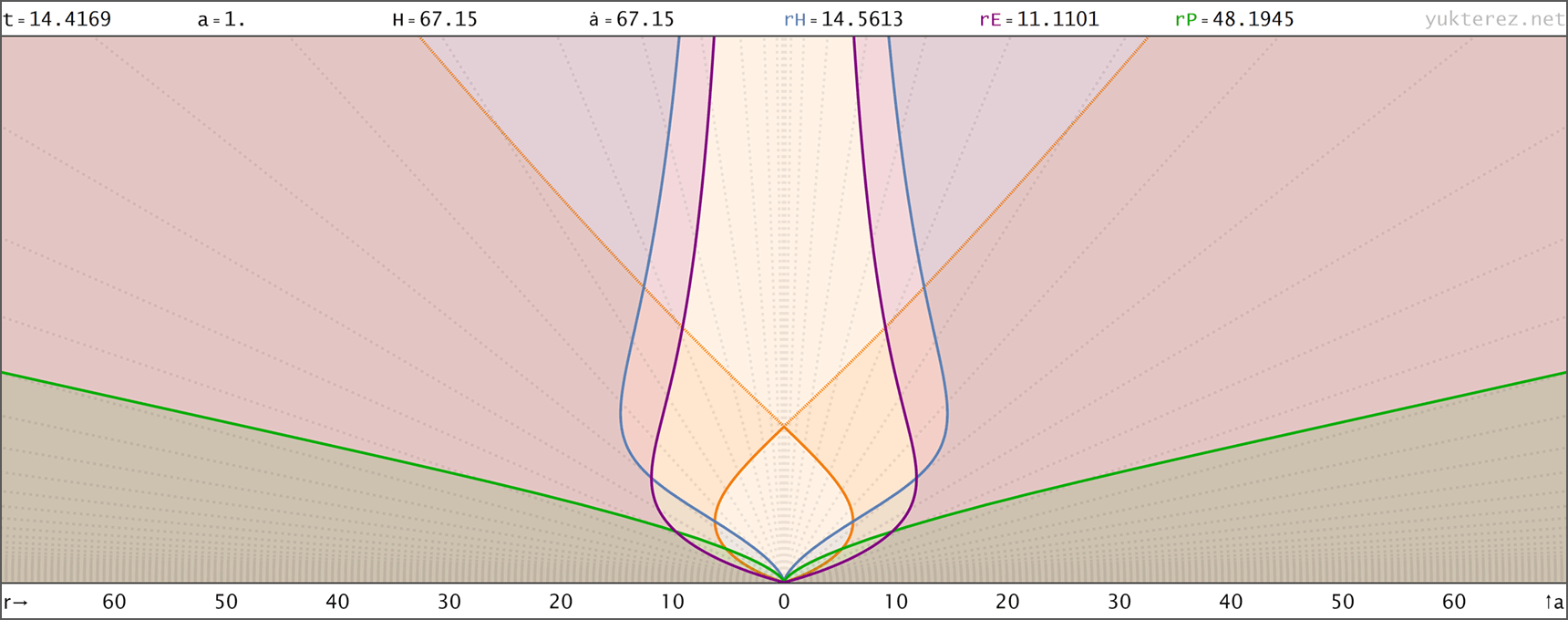
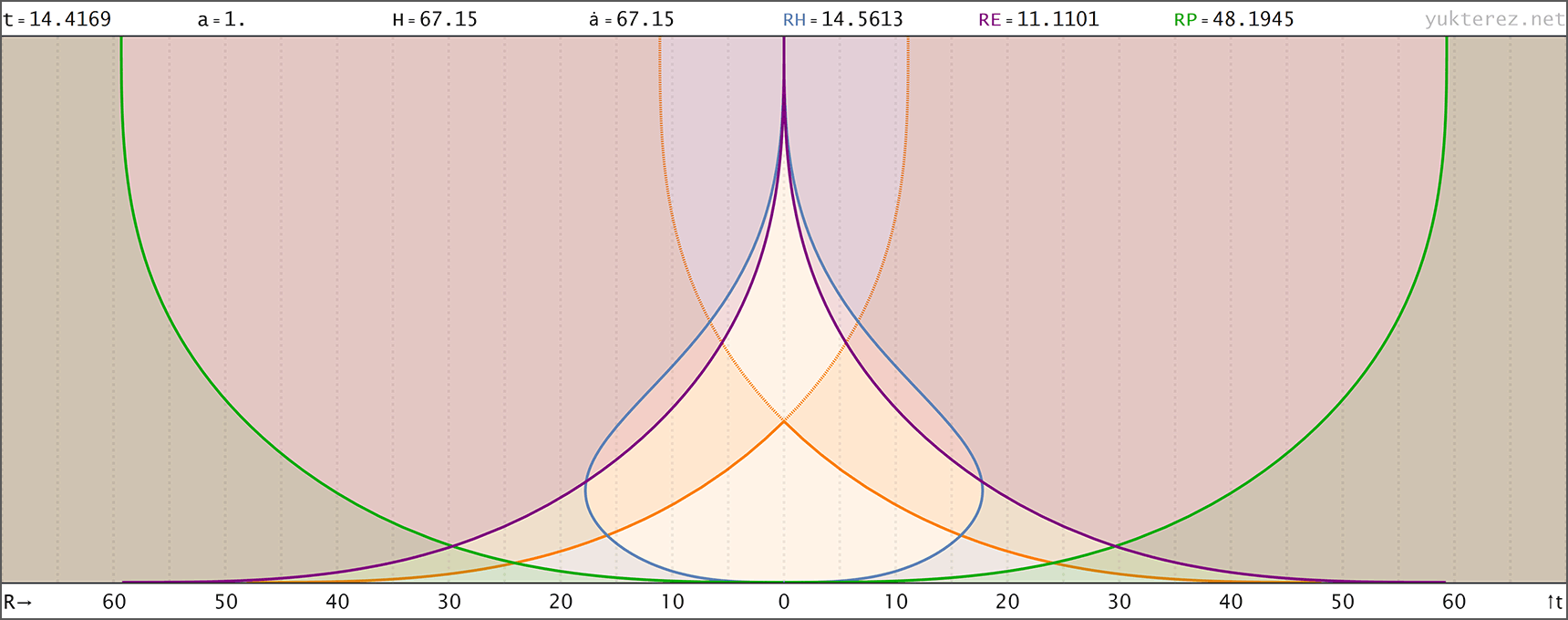
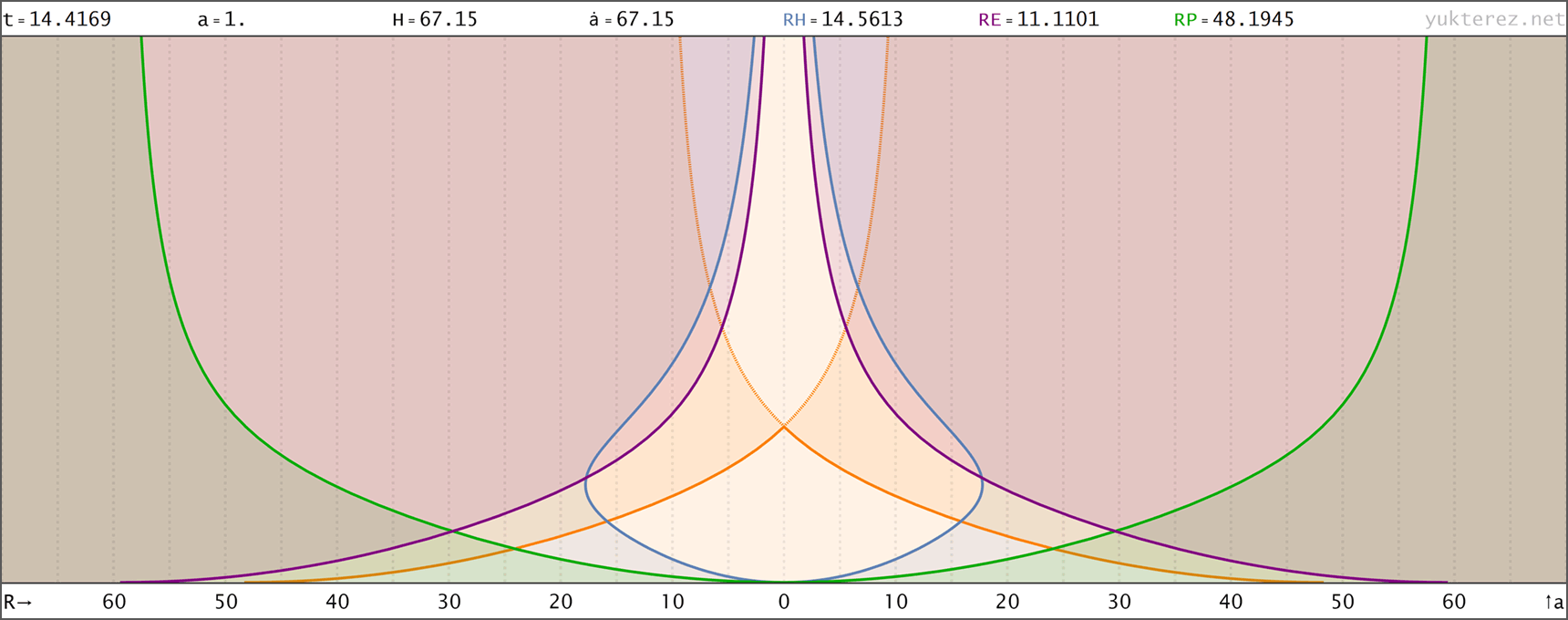
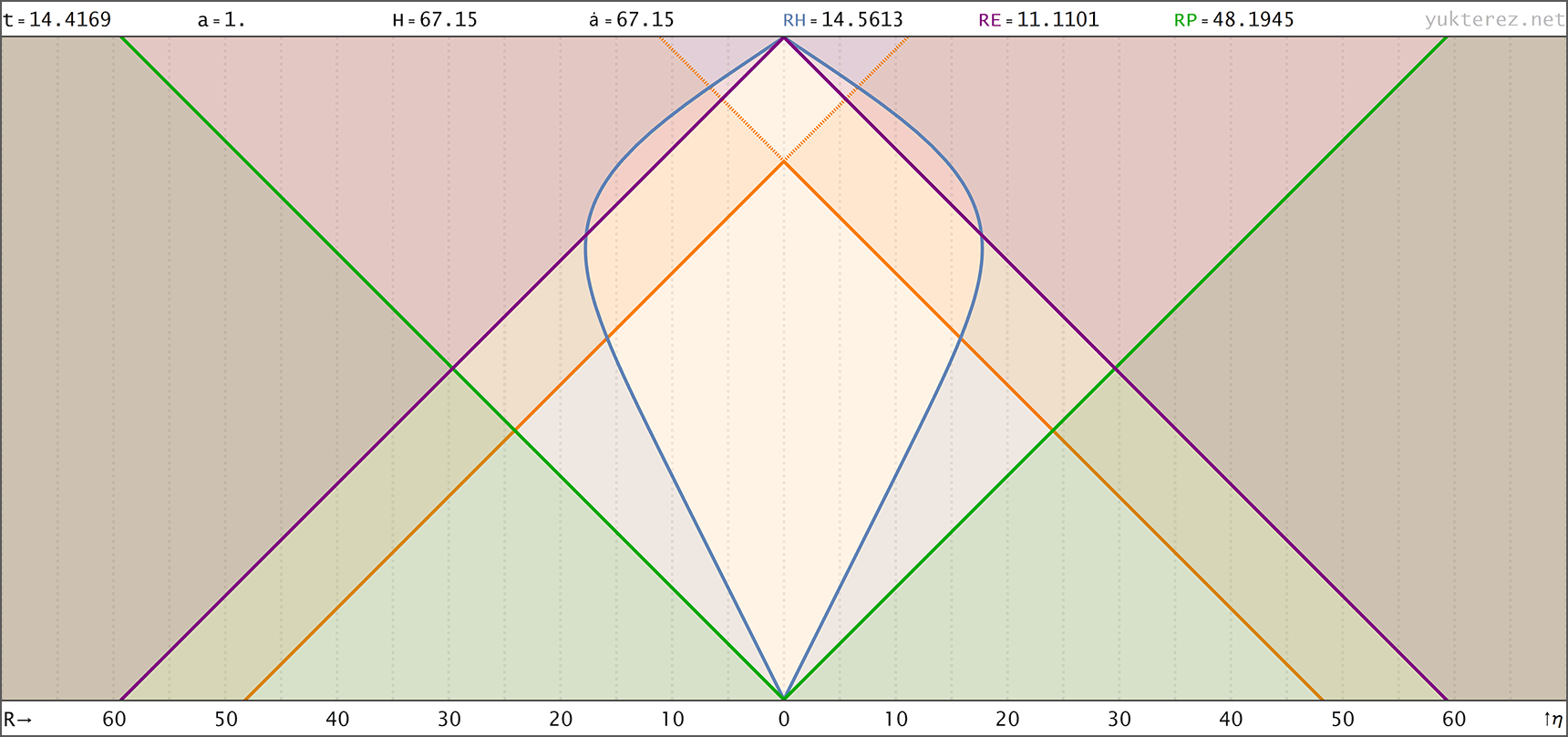
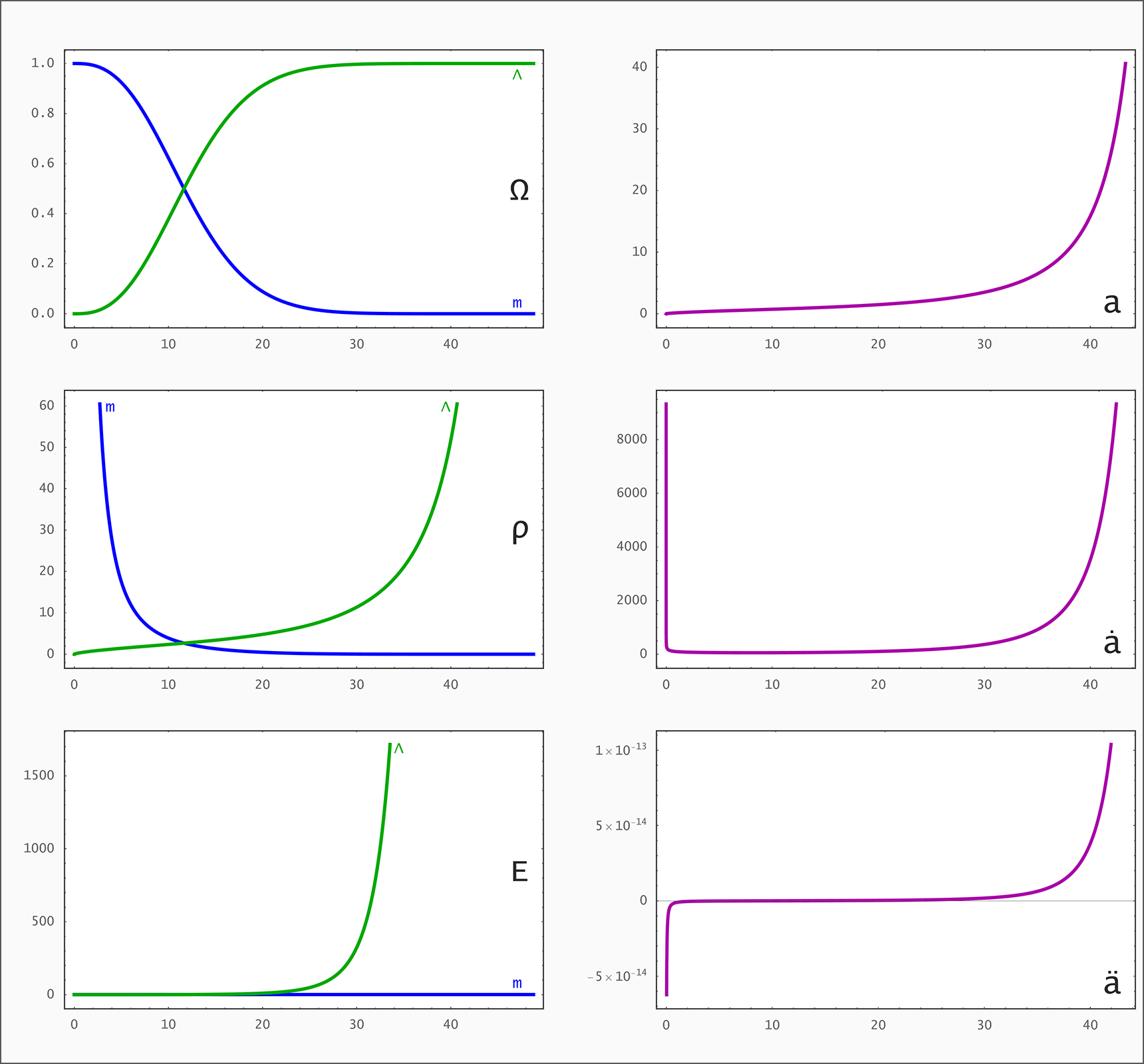
Für einen Vergleich mit unserem Universum wo H=H0·√[Ωr/a⁴+Ωm/a³+Ωk/a²+ΩΛ] siehe hier. Code:

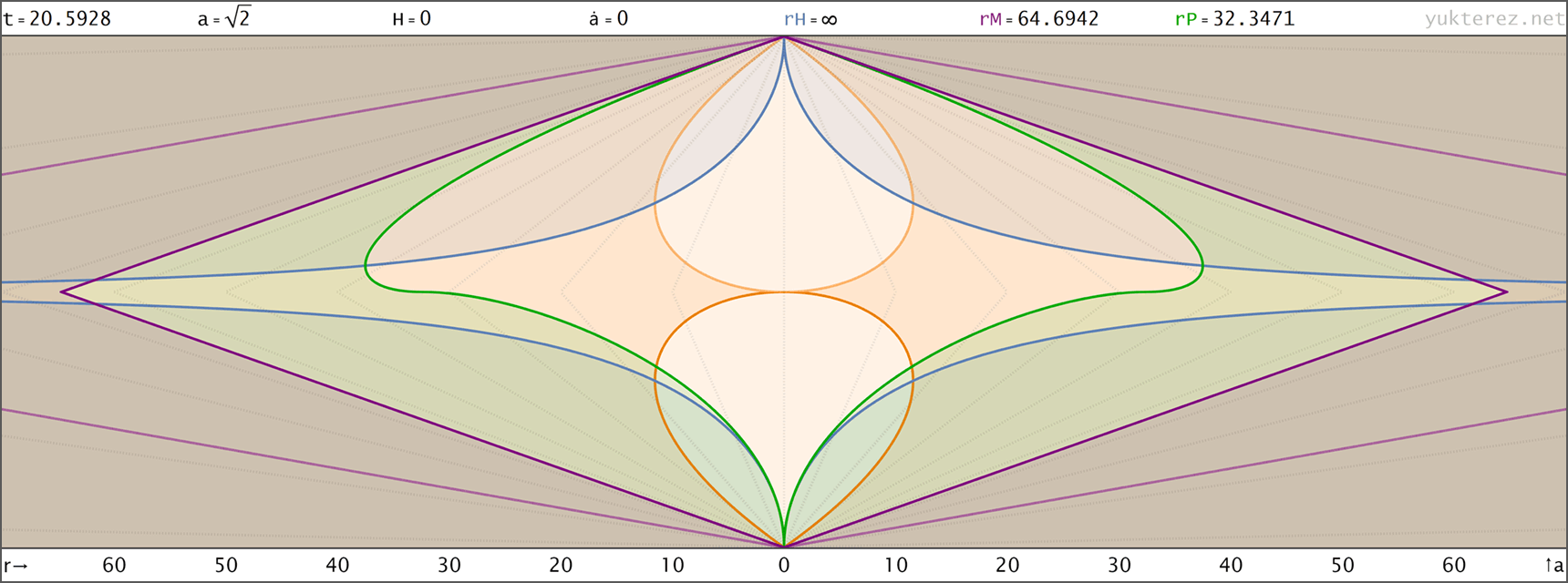
↑ proper, r(t) ◉ ↓ proper, r(a)

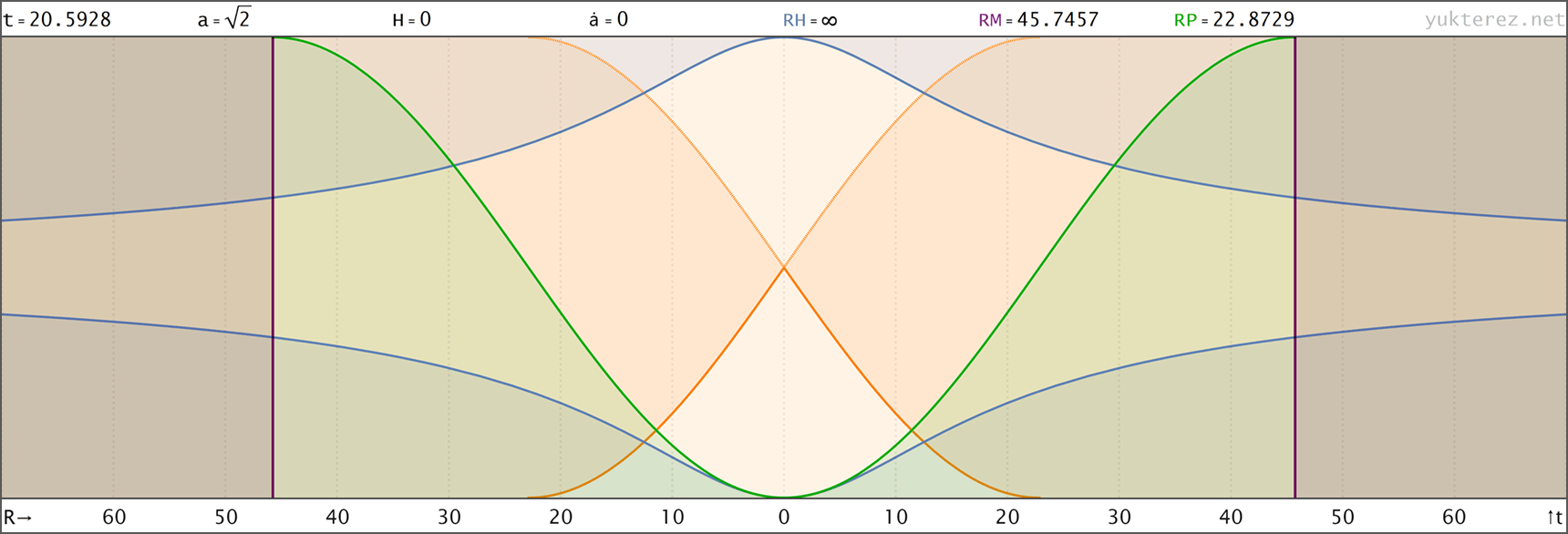
↑ proper, r(a) ◉ ↓ comoving, R(t)

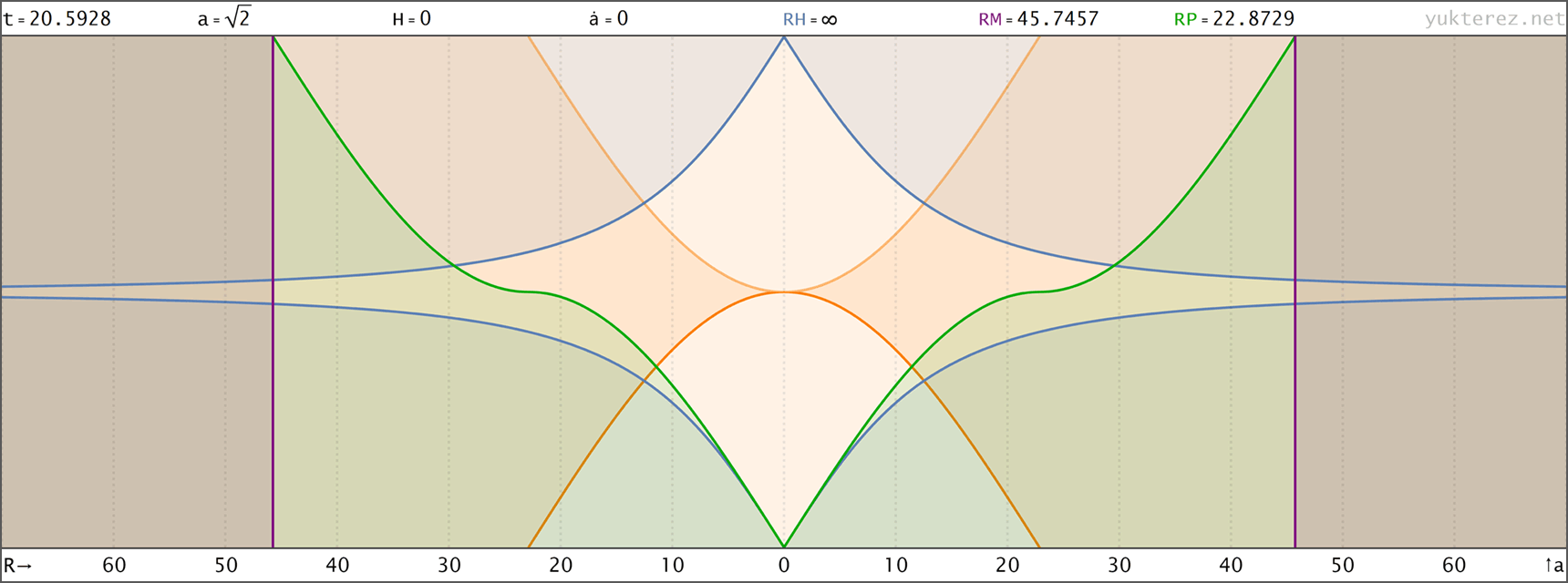
↑ comoving, R(t) ◉ ↓ comoving, R(a)

↑ comoving, R(a) ◉ ↓ conformal, R(η)

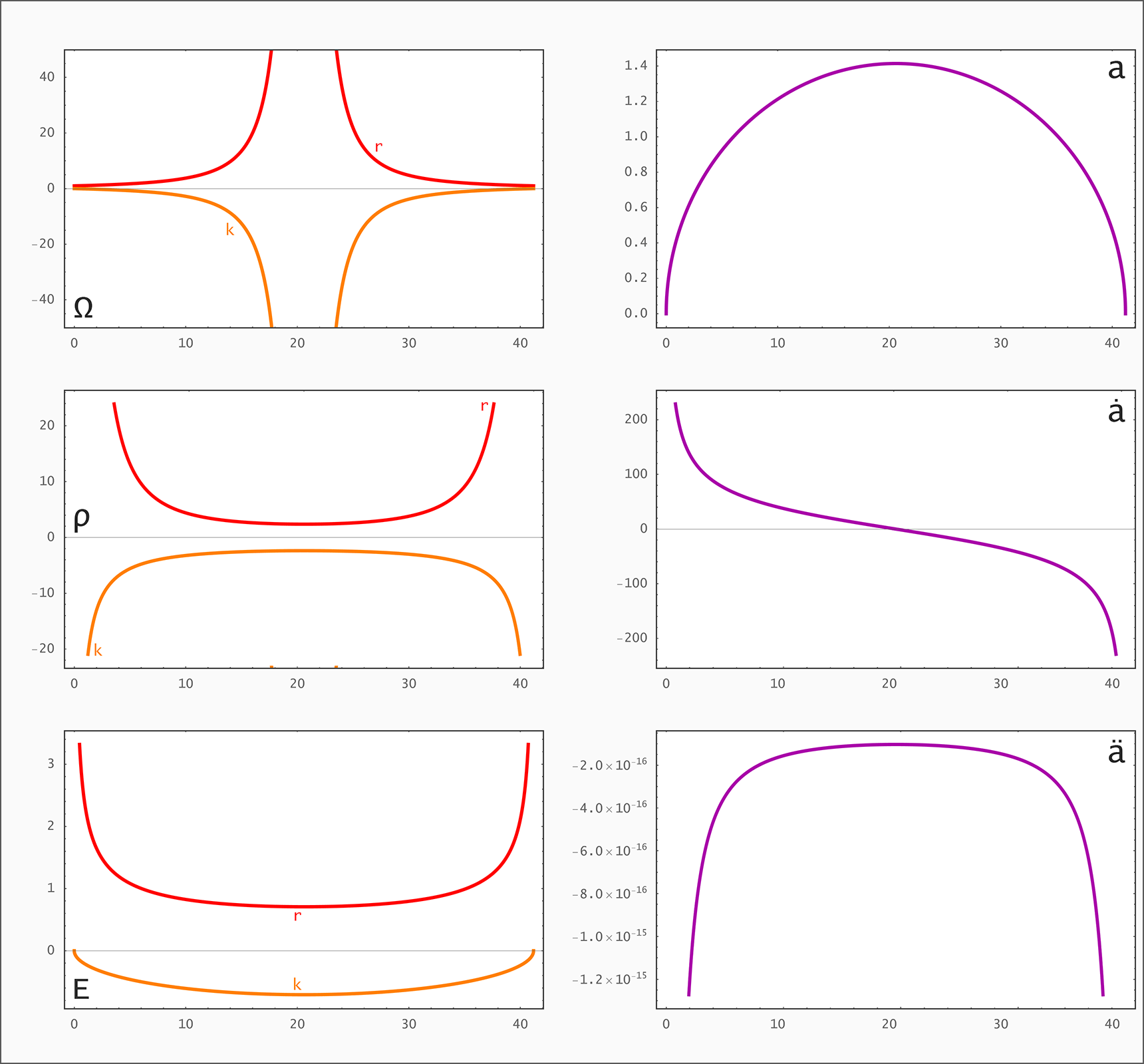
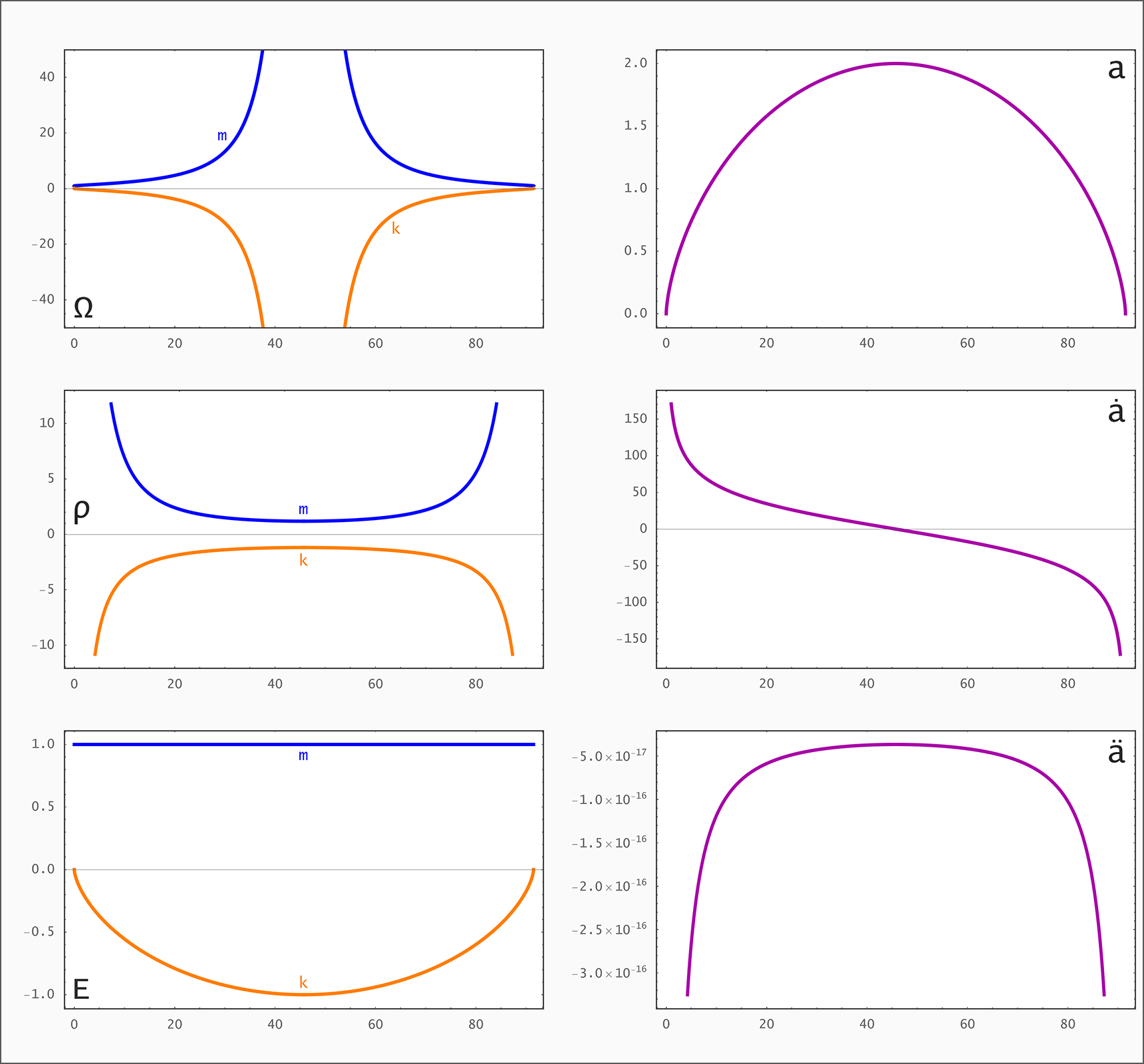
↑ Raumzeitdiagramme ◉ ↓ Ω, ρ, E, a, ȧ, ä als Funktionen von t

Für einen Vergleich mit unserem Universum wo H=H0·√[Ωr/a⁴+Ωm/a³+Ωk/a²+ΩΛ] siehe hier. Code:
Code: Alles auswählen
(* | Evolution of a Big Rip Universe | Simon Tyran, Vienna | www.yukterez.net | *)
set = {"GlobalAdaptive", "MaxErrorIncreases"->100,
Method->"GaussKronrodRule"}; (* Integration Rule *)
n = 100; (* Recursion Depth *)
int[f_, {x_, xmin_, xmax_}] := (* Integral *)
NIntegrate[f, {x, xmin, xmax},
Method->set, MaxRecursion->n, WorkingPrecision->wp];
wp = MachinePrecision; (* Working Precision *)
im = 320; (* Image Size *)
tMax = 1000 Gyr; TRip = tRip/Gyr; (* Integration Limit *)
prmax = 70; ptmax = TRip; (* Time Plot Range *)
c = 299792458 m/sek; (* Lightspeed *)
G = 667384*^-16 m^3 kg^-1 sek^-2; (* Newton Constant *)
Gyr = 10^7*36525*24*3600 sek; (* Billion Years *)
Glyr = Gyr*c; (* Billion Lightyears *)
Mpc = 30856775777948584200000 m; (* Megaparsec *)
kB = 13806488*^-30 kg m^2/sek^2/K; (* Boltzmann Constant *)
h = 662606957*^-42 kg m^2/sek; (* Planck Constant *)
ρc[H_] := 3H^2/8/π/G; (* Critical Density *)
ρR = 8π^5 kB^4 T^4/15/c^5/h^3; (* Radiation Density *)
ρΛ = ρc[H0] ΩΛ; (* Dark Energy Density *)
T = 2725/1000 K; (* CMB Temperature *)
kg = m = sek = 1; (* SI Units *)
ΩR = 0; (* Radiation Proportion including Neutrinos *)
ΩM = 315/1000; (* Matter Proportion including Dark Matter *)
ΩΛ = 1-ΩM-ΩR; (* Dark Energy Proportion *)
ΩT = ΩR+ΩM+ΩΛ; (* Total Density over Critical Density *)
ΩK = 1-ΩT; (* Curvature Density *)
H0 = 67150 m/Mpc/sek; (* Hubble Constant *)
H[a_] := H0 Sqrt[ΩR/a^4+ΩM/a^3+ΩK/a^2+ΩΛ*a] (* Hubble Parameter *)
sol = Quiet[NDSolve[{A'[t]/A[t] == H[A[t]], A[0] == 1*^-15},
A, {t, 0, tMax},
MaxSteps->∞, WorkingPrecision->wp,
StepMonitor :> (laststep=tRip; tRip=t;
stepsize=tRip-laststep;), Method->{"EventLocator",
"Event" :> (If[A[t]>10^1000, 0, 1])}]]; "tRip" -> TRip "Gyr"
a[t_] := Evaluate[(A[t]/.sol)[[1]]]; (* Scale Factor a by Time t *)
т[a_] := int[1/A/H[A], {A, 0, a}]; (* Time t by Scale Factor a *)
rP[t_] := a[t] int[c/a[т], {т, 0, t}]; (* Proper Particle Horizon by t *)
rp[a_] := a int[c/A^2/H[A], {A, 0, a}]; (* Proper Particle Horizon by a *)
RP[t_] := int[c/a[т], {т, 0, t}]; (* Comoving Particle Horizon by t *)
Rp[a_] := int[c/A^2/H[A], {A, 0, a}]; (* Comoving Particle Horizon by a *)
rE[t_] := a[t] int[c/a[т], {т, t, tRip}]; (* Proper Event Horizon by t *)
re[a_] := a int[c/A^2/H[A], {A, a, tRip}]; (* Proper Event Horizon by a *)
RE[t_] := int[c/a[т], {т, t, tRip}]; (* Comoving Event Horizon by t *)
Rε[a_] := int[c/A^2/H[A], {A, a, tRip}]; (* Comoving Event Horizon by a *)
rL[t0_, t_] := a[t] int[c/a[т], {т, t, t0}]; (* Proper Light Cone by t *)
rl[a0_, a_] := a int[c/A^2/H[A], {A, a, a0}]; (* Proper Light Cone by a *)
RL[t0_, t_] := int[c/a[т], {т, t, t0}]; (* Comoving Light Cone by t *)
Rl[a0_, a_] := int[c/A^2/H[A], {A, a, a0}]; (* Comoving Light Cone by a *)
rH[t_] := c/H[a[t]]; (* Proper Hubble Radius by t *)
rh[a_] := c/H[a]; (* Proper Hubble Radius by a *)
RH[t_] := c/H[a[t]]/a[t]; (* Comoving Hubble Radius by t *)
Rh[a_] := c/H[a]/a; (* Comoving Hubble Radius by a *)
ηmax = RP[tRip]/Glyr; "ηRip" -> ηmax "Gyr"
t0 = Re[t/.FindRoot[a[t]-1, {t, 10 Gyr}]]; ti = t Gyr; τi = τ Gyr;
"t0"->t0/Gyr "Gyr" (* Current Time *)
ã[η_] := Quiet[FindRoot[Rp[Ã]/Glyr-η, (* Scale Factor a by Conformal Time η *)
{Ã, 0.00001}, WorkingPrecision->wp, MaxIterations->1000][[1, 2]]];
ā = Quiet[Interpolation[Join[{{0, 0}},
ParallelTable[{((Sin[η π/ηmax-π/2]+1) ηmax/2),
ã[((Sin[η π/ηmax-π/2]+1) ηmax/2)]}, {η, ηmax/im, ηmax, ηmax/im}]]]];
Ť[η_] := Quiet[FindRoot[RP[τ Gyr]/Glyr-η, (* t by η *)
{τ, 1}, WorkingPrecision->wp, MaxIterations->1000][[1, 2]]]
(* ţ = Quiet[Interpolation[Join[{{0, 0}},
ParallelTable[{((Sin[η π/ηmax-π/2]+1) ηmax/2),
Ť[((Sin[η π/ηmax-π/2]+1) ηmax/2)]}, {η, ηmax/im, ηmax, ηmax/im}]]]]; *)
rpN = Rp[1]/Glyr;
"PROPER DISTANCES, f(t)"
pt = Quiet[Plot[
{rH[τi]/Glyr, rP[τi]/Glyr, rE[τi]/Glyr},
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot1[t_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[
{rL[ti, τi]/Glyr, -rL[ti, τi]/Glyr},
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], pt]], 90 Degree]}}]];
Do[Print[plot1[t]], {t, {t0/Gyr}}]
plot2 = Rasterize[Grid[{{Rotate[Quiet[Plot[
Join[{0}, Table[a[τ Gyr] n^(7/2)/250, {n, 1, 55, 1}]],
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"COMOVING DISTANCES, f(t)"
ct = Quiet[Plot[
{rH[τi]/(a[τi]Glyr), rP[τi]/(a[τi]Glyr), rE[τi]/(a[τi]Glyr)},
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot3[t_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[
{rL[ti, τi]/(a[τi]Glyr), -rL[ti, τi]/(a[τi]Glyr)},
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], ct]], 90 Degree]}}]];
Do[Print[plot3[t]], {t, {t0/Gyr}}]
plot4 = Rasterize[Grid[{{Rotate[Quiet[Plot[
Join[{0}, Table[n, {n, 10, 100, 10}]],
{τ, 0, ptmax}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, ptmax}, {0, prmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"PROPER DISTANCES, f(a)"
pa = Quiet[Plot[
{rh[α]/Glyr, rp[α]/Glyr, re[α]/Glyr},
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot5[å_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[
{rl[å, α]/Glyr, -rl[å, α]/Glyr},
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], pa]], 90 Degree]}}]];
Do[Print[plot5[å]], {å, {1}}]
plot6 = Rasterize[Grid[{{Rotate[Quiet[Plot[
Join[{0}, Table[α n^(7/2)/250, {n, 1, 55, 1}]],
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"COMOVING DISTANCES, f(a)"
ca = Quiet[Plot[
{rh[α]/Glyr/α, rp[α]/Glyr/α, re[α]/Glyr/α},
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot7[å_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[
{rl[å, α]/Glyr/α, -rl[å, α]/Glyr/α},
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], ca]], 90 Degree]}}]];
Do[Print[plot7[å]], {å, {1}}]
plot8 = Rasterize[Grid[{{Rotate[Quiet[Plot[
Join[{0}, Table[n, {n, 10, 100, 10}]],
{α, 0, prmax Gyr/t0}, Frame->True, AspectRatio->prmax/ptmax,
FrameTicks->None, PlotRange->{{0, prmax Gyr/t0}, {0, prmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"CONFORMAL DIAGRAM, f(η)"
cη = Quiet[Plot[
{Rh[ā[Ct]]/Glyr, Ct, Rε[ā[Ct]]/Glyr},
{Ct, 0, ηmax}, Frame->True, AspectRatio->prmax/ηmax,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, prmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot9[η_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[
{η-Ct, Ct-η}, {Ct, 0, ηmax},
Frame->True, AspectRatio->prmax/ηmax,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, prmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], cη]], 90 Degree]}}]];
Do[Print[plot9[η]], {η, {rpN}}]
plot10 = Rasterize[Grid[{{Rotate[Quiet[Plot[
Join[{0}, Table[n, {n, 10, 100, 10}]],
{Ct, 0, ηmax}, Frame->True, AspectRatio->prmax/ηmax,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, prmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
s[text_] := Style[text, FontFamily->"Lucida Console", FontSize->36]