Schwarzschild De Sitter Metric
Verfasst: Mo 17. Feb 2020, 21:32

 This is the english version.
This is the english version.  Deutschsprachige Version: hier entlang
Deutschsprachige Version: hier entlang
The Schwarzschild De Sitter metric can be used to study the gravity of a dominant mass in an expanding universe:

The critical mass at which the black hole horizon coincides with the cosmic event horizon (the Nariai limit) is
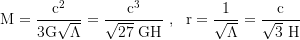
where the radii of the horizons are derived by setting
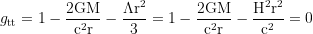
and solving for the positive solutions for r.

The maximal mass of a black hole in a De Sitter universe with our cosmological constant that is Λ≈1e-52/m² would be ≈4.3e52kg:


The critical mass at which the black hole horizon coincides with the cosmic event horizon (the Nariai limit) is
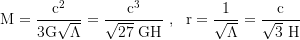
where the radii of the horizons are derived by setting
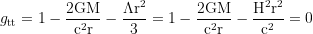
and solving for the positive solutions for r.

The maximal mass of a black hole in a De Sitter universe with our cosmological constant that is Λ≈1e-52/m² would be ≈4.3e52kg:

x-axis: M (in kg), y-axis: r (in GLyr); green/blue: horizons (cosmic event horizon and black hole horizon), red: Schwarzschild radius rs

The attraction of a galaxy like ours is offset by the expansion of the universe at a distance of about 1 megaparsec, so that a test particle that is at that distance from the galaxy is attracted by it as much as it is accelerated away from it by the dark energy.
The physical distance of a test particle from the dominant mass remains constant at the equilibrium radius. If the dominant mass rests relative to the background radiation, i.e. flows with the Hubbleflow, our stationary test particle can no longer also rest relative to the background radiation, since it is not flowing with the Hubble flow when it is stationary with respect to the central mass.
Equilibrium radius: the neutonian orbital velocity is set equal to the vacuum recession velocity and resolved to r:


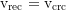


Derivation: the equilibrium radius at which a test particle remains stationary relative to the dominant mass is, with

and the resulting radial component of the four-acceleration

which is set to 0 and resolved to r, at

In a De Sitter universe, the relation between the Hubble constant and the cosmological constant is

plugging that into the solution for the equilibrium radius, we get the solution obtained above


For a circular orbit around the dominant mass we set
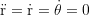
and solve for v:

which is an angular velocity of

where for brevity we use the dimensionless length and cosmological constant


The local escape velocity relative to a stationary buoy is with

or E=-pt=mc² and resolved to v

where the minimum is always greater than 0 and lies at the equilibrium radius mentioned above, where it is
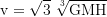
For an observer who is traveling with the escape velocity, the gravitational and the kinematic time dilation balance out, so that
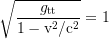
The frames of those local observers build the hypersurface of constant t in comoving coordinates, while in the Droste style coordinates here the local clocks and rulers are stationary with respect to the center.

Recessional velocity of free-falling test particles that arise near the equilibrium radius (in natural units of G=M=c=1 und Λ=0.01):

The physical distance of a test particle from the dominant mass remains constant at the equilibrium radius. If the dominant mass rests relative to the background radiation, i.e. flows with the Hubbleflow, our stationary test particle can no longer also rest relative to the background radiation, since it is not flowing with the Hubble flow when it is stationary with respect to the central mass.
Equilibrium radius: the neutonian orbital velocity is set equal to the vacuum recession velocity and resolved to r:


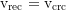


Derivation: the equilibrium radius at which a test particle remains stationary relative to the dominant mass is, with

and the resulting radial component of the four-acceleration

which is set to 0 and resolved to r, at

In a De Sitter universe, the relation between the Hubble constant and the cosmological constant is

plugging that into the solution for the equilibrium radius, we get the solution obtained above


For a circular orbit around the dominant mass we set
and solve for v:

which is an angular velocity of

where for brevity we use the dimensionless length and cosmological constant


The local escape velocity relative to a stationary buoy is with

or E=-pt=mc² and resolved to v

where the minimum is always greater than 0 and lies at the equilibrium radius mentioned above, where it is
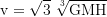
For an observer who is traveling with the escape velocity, the gravitational and the kinematic time dilation balance out, so that
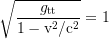
The frames of those local observers build the hypersurface of constant t in comoving coordinates, while in the Droste style coordinates here the local clocks and rulers are stationary with respect to the center.

Recessional velocity of free-falling test particles that arise near the equilibrium radius (in natural units of G=M=c=1 und Λ=0.01):

x-axis: r (in GM/c²), y-axis: v (in c); red: recessional velocity relative to stationary Fidos, green: velocity of an E=mc² particle. Λ=c⁴/G²/M²/100=1/rs²/25
