 Mollweide
MollweideWelt- oder Himmelskarten liegen gängigerweise entweder in der Plattkarten- oder der Mollweide-Projektion vor. Der folgende Artikel zeigt wie man einen Kartennetzentwurf in den anderen umwandelt, und wie man ihn auf eine Kugel projiziert. Das in den Beispielen verwendete Rohmaterial ist das Wikipedia-Bild Equirectangular-projection.jpg
Zuerst wird die Funktion für die Koordinatentransformation definiert und ihr der Name Eq2Mol zugewiesen:
Code: Alles auswählen
Eq2Mol[{x_, y_}] := {Lmol[x, y], Bmol[y]};
θ[y_, rad_: 1] := ArcSin[y];
Bmol[y_] := ArcSin[(2 θ[y] + Sin[2 θ[y]])/π];
Lmol[x_, y_] := 0 + π x/(2 Cos[θ[y]]);
(* Equirectangular <> Mollweide *)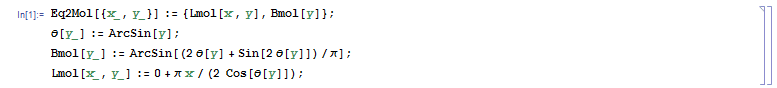
Anstatt der 0 kann auch der Winkel um den der Längengrad verschoben werden soll in Radianten eingegeben werden. Dann wird eine Karte geladen, in diesem Fall eine Plattkarte, und dem Bild eine beliebige Variable, hier Eq für Equirectangular, zugewiesen:
Code: Alles auswählen
Eq = Import["http://upload.wikimedia.org/wikipedia/commons/e/ea/Equirectangular-projection.jpg"]
(* Plattkarte laden *)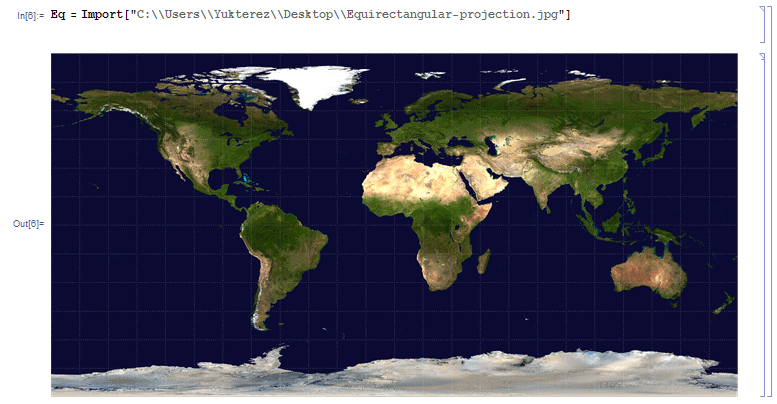
Die Plattkarte Eq wird ins Mollweide-Format umgewandelt und das generierte Bild als Mw gespeichert:
Code: Alles auswählen
Mw = ImageTransformation[Eq, Eq2Mol,
DataRange -> {{-π, π}, {-π/2, π/2}},
PlotRange -> {{-2, 2}, {-1, 1}}]
(* Equirectangular -> Mollweide *)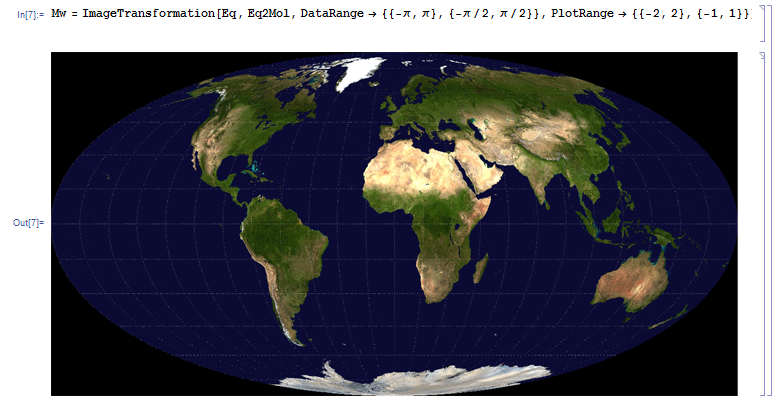
Und umgekehrt von Mollweide wieder zurück nach Equirectangular als eQ:
Code: Alles auswählen
eQ = ImageForwardTransformation[Mw, Eq2Mol,
DataRange -> {{-2, 2}, {-1, 1}},
PlotRange -> All]
(* Mollweide -> Equirectangular *)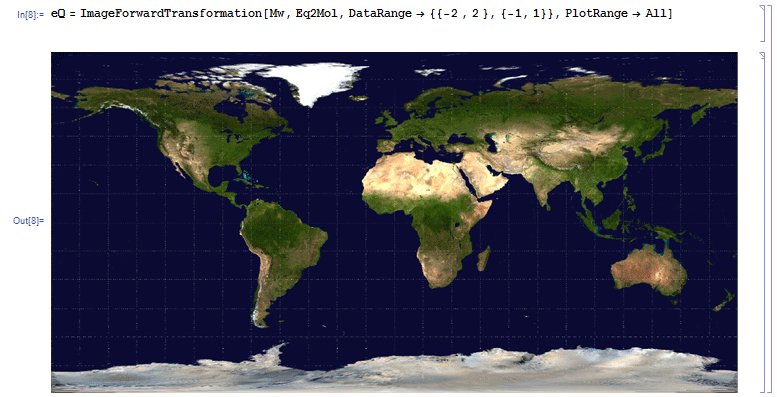
Da es sich um eine Pixeloperation handelt werden die Qualitätsverluste desto höher je öfter man von einer Projektion in die andere und wieder zurück transformiert.image transformation bildtransformation bild mathematica geographie



























