Pendel: Position nach Zeit
Verfasst: So 20. Mär 2016, 05:13
von Yukterez
Inhalt:
1) kleine Amplituden
2) beliebig hohe Amplituden
3) Pendel mit v0 und Überschlag
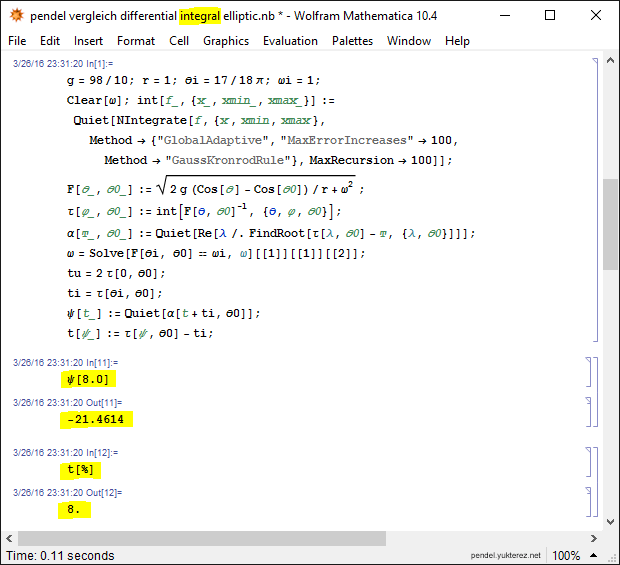
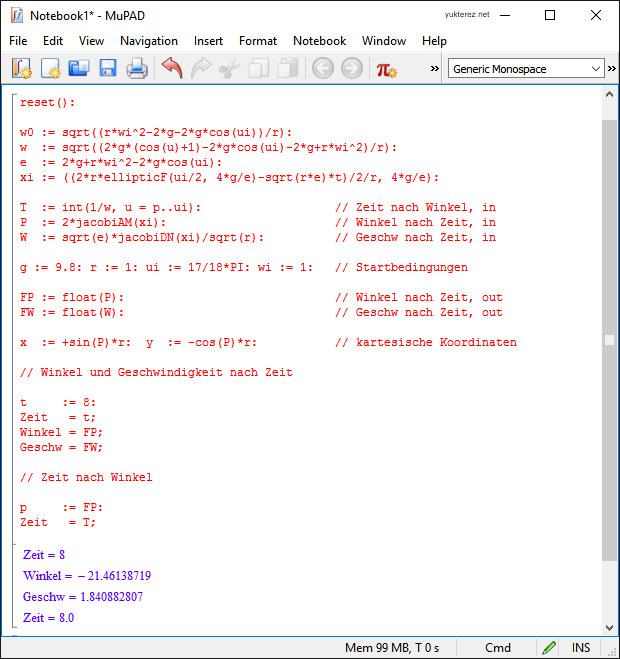
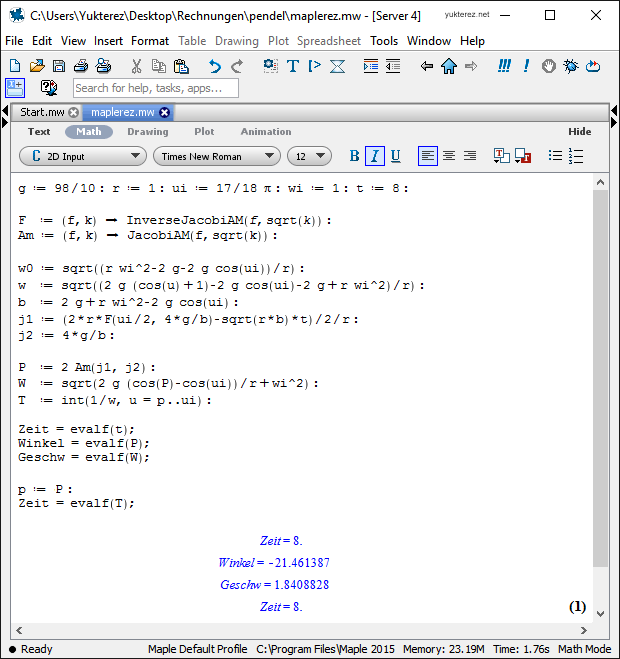
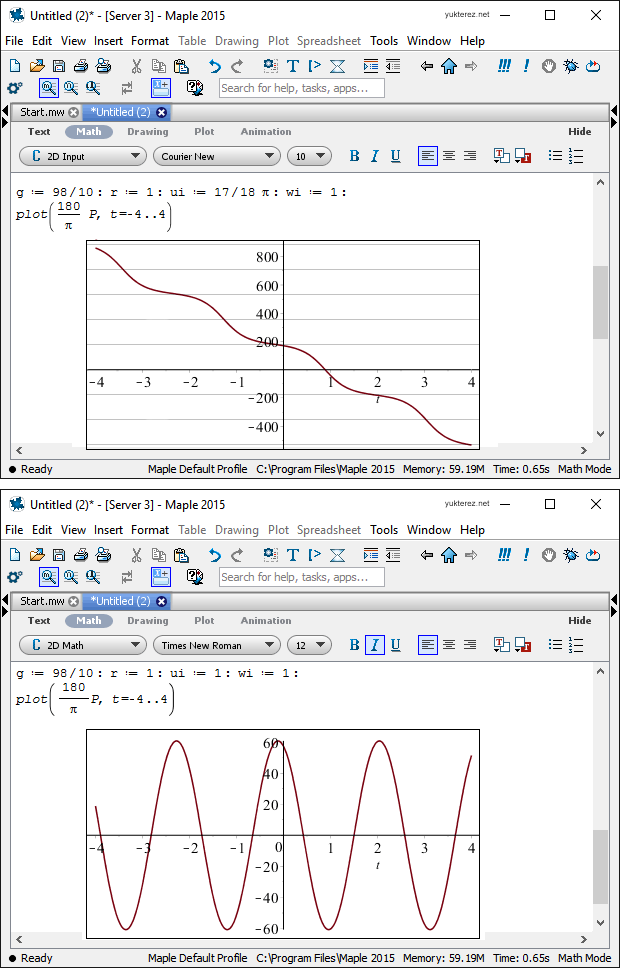
4) verschiedene Methoden
5) unterschiedliche Syntax

1) vereinfachte Formel für kleine Amplituden
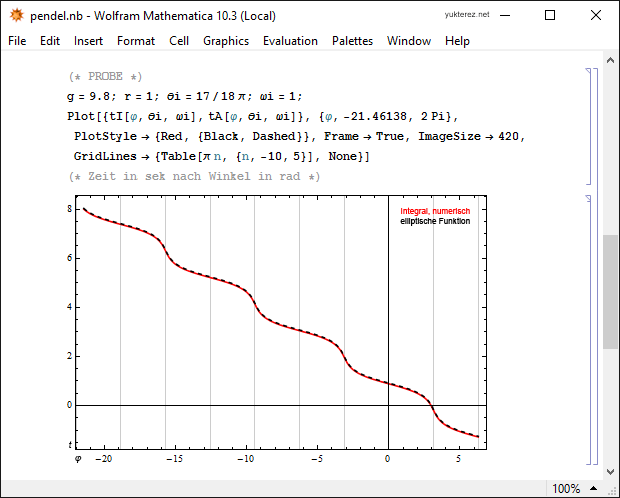
Winkel nach Zeit:
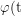=\theta_0\cdot \cos \left(t\cdot \sqrt{g/r}\right))
Periodendauer:
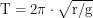
Bei einem Pendel mit Trägheitsmoment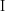 und Masse
und Masse 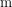 wird der Term
wird der Term 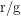 einfach durch
einfach durch 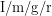 ersetzt, und
ersetzt, und 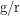 durch den Kehrwert.
durch den Kehrwert.
Wenn die initialen Winkel klein sind können die höheren Terme vernachlässigt werden und die Schwingungsdauer ist für alle Pendel annähernd gleich. Bei höheren Winkeln muss die so erhaltene Periodendauer mit dem passenden Faktor multipliziert werden. Tabelle:
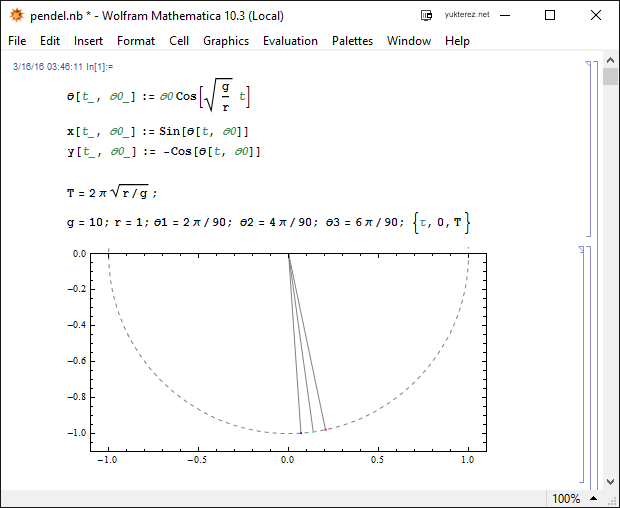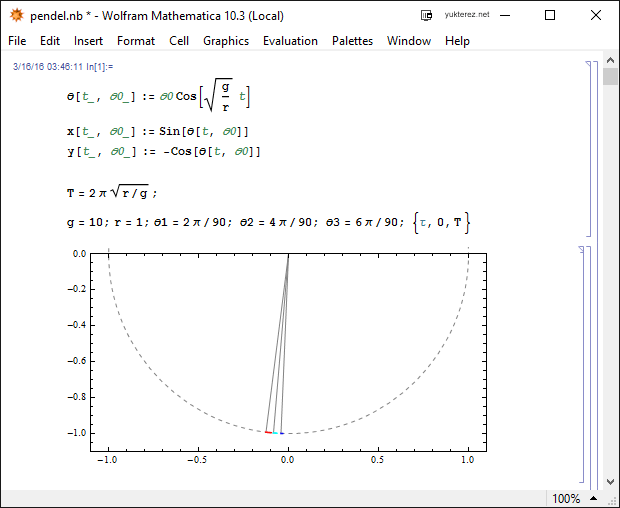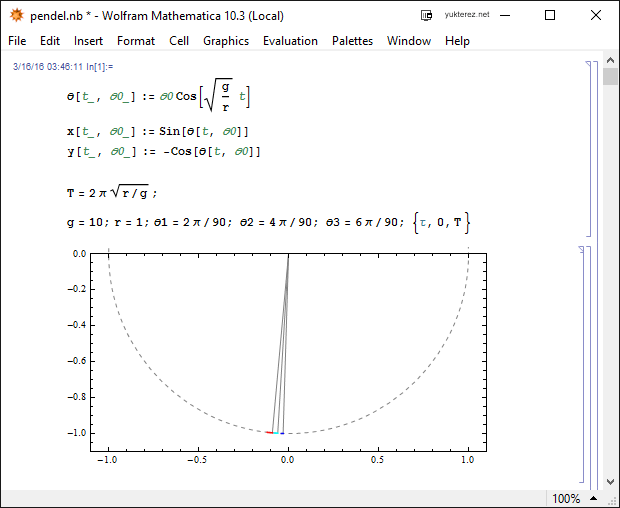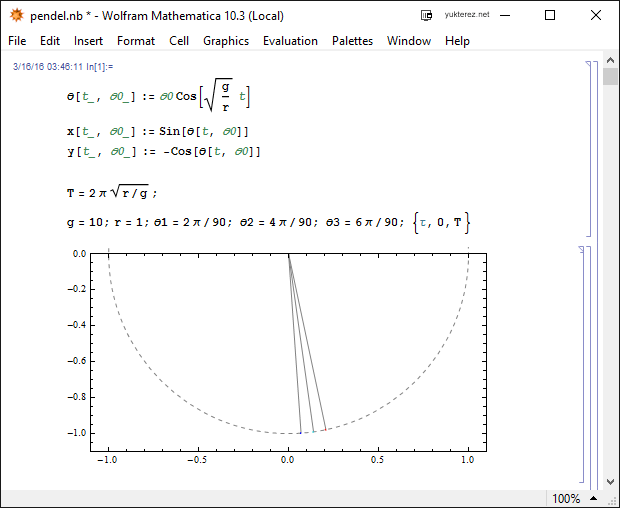
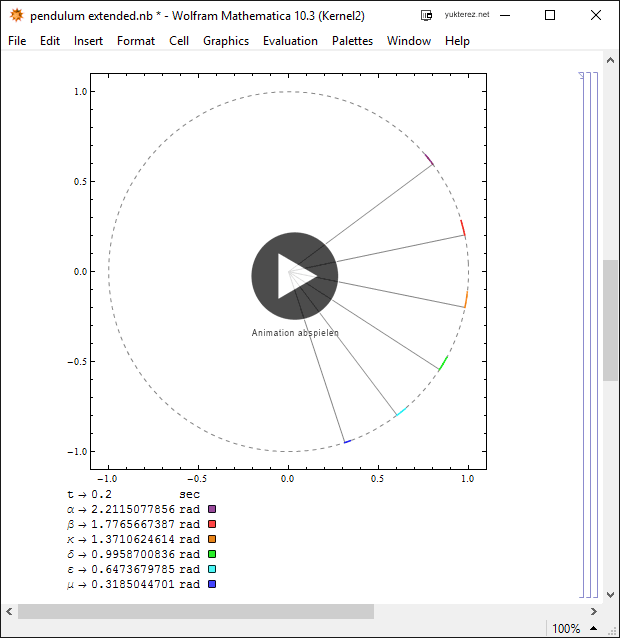
Die Winkel sind in Radianten angegeben. Die Schweiflänge ist 1/20 Sekunde (je höher die Geschwindigkeit desto länger der Schweif).
Code:
1) kleine Amplituden
2) beliebig hohe Amplituden
3) Pendel mit v0 und Überschlag
4) verschiedene Methoden
5) unterschiedliche Syntax

1) vereinfachte Formel für kleine Amplituden
Winkel nach Zeit:
Periodendauer:
Bei einem Pendel mit Trägheitsmoment
Wenn die initialen Winkel klein sind können die höheren Terme vernachlässigt werden und die Schwingungsdauer ist für alle Pendel annähernd gleich. Bei höheren Winkeln muss die so erhaltene Periodendauer mit dem passenden Faktor multipliziert werden. Tabelle:
Code: Alles auswählen
(* kurze Tabelle *)
~0° → 1.00000 90° → 1.18034
10° → 1.00191 100° → 1.23223
20° → 1.00767 110° → 1.29534
30° → 1.01741 120° → 1.37288
40° → 1.03134 130° → 1.46982
50° → 1.04978 140° → 1.59445
60° → 1.07318 150° → 1.76220
70° → 1.10214 160° → 2.00751
80° → 1.13749 170° → 2.43936Code: Alles auswählen
(* ausführliche Tabelle *)
~0° → 1.000000000000000
1° → 1.000019036394853
2° → 1.000076157146139
3° → 1.000171368451913
4° → 1.000304699971725
5° → 1.000476167963778
6° → 1.000685814346354
7° → 1.000933688079555
8° → 1.001219829830915
9° → 1.001544305521280
10° → 1.001907183611697
11° → 1.002308540450655
12° → 1.002748460652199
13° → 1.003227037116312
14° → 1.003744376422762
15° → 1.004300572166438
16° → 1.004895763224550
17° → 1.005530056583036
18° → 1.006203605860836
19° → 1.006916545781318
20° → 1.007669021225375
21° → 1.008461209552825
22° → 1.009293266387560
23° → 1.010165379034360
24° → 1.011077742065479
25° → 1.012030547305509
26° → 1.013023996117529
27° → 1.014058317755816
28° → 1.015133732892565
29° → 1.016250478513536
30° → 1.017408790466781
31° → 1.018608946907674
32° → 1.019851204561895
33° → 1.021135831696900
34° → 1.022463135318085
35° → 1.023833405603545
36° → 1.025246953006698
37° → 1.026704099916710
38° → 1.028205177446780
39° → 1.029750532992619
40° → 1.031340514419446
41° → 1.032975507739290
42° → 1.034655886242134
43° → 1.036382044978473
44° → 1.038154384002293
45° → 1.039973339336188
46° → 1.041839331538550
47° → 1.043752829641255
48° → 1.045714269941229
49° → 1.047724144334561
50° → 1.049782957472202
51° → 1.051891192901066
52° → 1.054049393651034
53° → 1.056258093964219
54° → 1.058517851053000
55° → 1.060829239323839
56° → 1.063192850370202
57° → 1.065609289008816
58° → 1.068079201224310
59° → 1.070603206013567
60° → 1.073181999488621
61° → 1.075816258288423
62° → 1.078506691238612
63° → 1.081254028715914
64° → 1.084059023331366
65° → 1.086922450245202
66° → 1.089845099100240
67° → 1.092827823046708
68° → 1.095871430716286
69° → 1.098976837241281
70° → 1.102144903267401
71° → 1.105376588931165
72° → 1.108672841988429
73° → 1.112034650198573
74° → 1.115463032681171
75° → 1.118959037463299
76° → 1.122523750419182
77° → 1.126158278828253
78° → 1.129863803491582
79° → 1.133641476737052
80° → 1.137492554541896
81° → 1.141418294934036
82° → 1.145420006456775
83° → 1.149499040502052
84° → 1.153656791942088
85° → 1.157894695102081
86° → 1.162214265214344
87° → 1.166617007756526
88° → 1.171104540786880
89° → 1.175678502013516
90° → 1.180340594425066
91° → 1.18509258007326
92° → 1.189936274392363
93° → 1.194873589772660
94° → 1.199906457367066
95° → 1.205036910701758
96° → 1.210267040535012
97° → 1.215599039412496
98° → 1.221035148096657
99° → 1.226577738865578
100° → 1.232229192807593
101° → 1.237992065516499
102° → 1.243868959956808
103° → 1.249862614454843
104° → 1.255975850742244
105° → 1.262211619759275
106° → 1.268572959436030
107° → 1.275063081373486
108° → 1.281685297299368
109° → 1.288443058823340
110° → 1.295339995543692
111° → 1.302379847321552
112° → 1.309566545783780
113° → 1.316904187075688
114° → 1.324397070831620
115° → 1.332049670092574
116° → 1.339866681146829
117° → 1.347852988308526
118° → 1.356013750916653
119° → 1.364354375905023
120° → 1.372880489784419
121° → 1.381598064405037
122° → 1.390513311685838
123° → 1.399632828598414
124° → 1.408963495225475
125° → 1.418512609564637
126° → 1.428287865168193
127° → 1.438297353185673
128° → 1.448549620406017
129° → 1.459053741540671
130° → 1.469819323036506
131° → 1.480856499466419
132° → 1.492176075444971
133° → 1.503789528604213
134° → 1.515709039559779
135° → 1.527947581547664
136° → 1.540519028866836
137° → 1.553438200870597
138° → 1.566720919676694
139° → 1.580384138009136
140° → 1.594446090281888
141° → 1.608926378236135
142° → 1.623846065549431
143° → 1.639227938608345
144° → 1.655096637173628
145° → 1.671478831026229
146° → 1.688403487076955
147° → 1.705902182659665
148° → 1.724009385861411
149° → 1.742762759274199
150° → 1.762203727208658
151° → 1.782377812317203
152° → 1.803335374720997
153° → 1.825132152362303
154° → 1.847830214256532
155° → 1.871498885603637
156° → 1.896215892146506
157° → 1.922068829545972
158° → 1.949156957465596
159° → 1.977593304768987
160° → 2.007507388328621
161° → 2.039048535490428
162° → 2.072390206934585
163° → 2.107735562577612
164° → 2.145324607053039
165° → 2.185443629799353
166° → 2.228438168426636
167° → 2.274730356263068
168° → 2.324843711090852
169° → 2.379438219330666
170° → 2.439362688586132
171° → 2.505734408965678
172° → 2.580065984832729
173° → 2.664477435263426
174° → 2.762072874386099
175° → 2.877663500974635
176° → 3.019307534679719
177° → 3.202108845344259
178° → 3.459971016667659
179° → 3.901065035739219
180° → instab. GleichgewCode: Alles auswählen
(* Code zur Tabelle *)
set = {"GlobalAdaptive", "MaxErrorIncreases" -> 100, Method -> "GaussKronrodRule"}; n = 100; int[f_, {x_, xmin_, xmax_}] := Quiet[NIntegrate[f, {x, xmin, xmax}, Method -> set, MaxRecursion -> n]]; g = 10; r = 1; t[φ_, θ0_] := Sqrt[r/(2 g)] int[1/Sqrt[Cos[θ] - Cos[θ0]], {θ, φ, θ0}]; TU[θ0_] := 4 t[0, θ0]; Tu = 2 π Sqrt[r/g]; Do[Print[N[w 180/π] -> TU[w]/Tu], {w, 0, π, π/18}]
Die Winkel sind in Radianten angegeben. Die Schweiflänge ist 1/20 Sekunde (je höher die Geschwindigkeit desto länger der Schweif).
Code:
Code:mathematisches und physikalisches Pendel
Code: Alles auswählen
(* Syntax: Mathematica || yukterez.net *)
θ[t_, θ0_] := θ0 Cos[Sqrt[g/r] t]
x[t_, θ0_] := +Sin[θ[t, θ0]] r
y[t_, θ0_] := -Cos[θ[t, θ0]] r
g = 10; r = 1; θ1 = 2 π/90; θ2 = 4 π/90; θ3 = 6 π/90;
Do[Print[Rasterize[Grid[{{Show[
Graphics[
{LightGray, Line[{{0, 0}, {x[τ, θ1], y[τ, θ1]}}]},
PlotRange -> {{-1.1 r, 1.1 r}, {-1.1 r, 0 r}},
Frame -> True, ImageSize -> 420],
Graphics[
{LightGray, Line[{{0, 0}, {x[τ, θ2], y[τ, θ2]}}]}],
Graphics[
{LightGray, Line[{{0, 0}, {x[τ, θ3], y[τ, θ3]}}]}],
Graphics[{LightGray, Dashed, Circle[]}],
ParametricPlot[{
{x[t, θ3], y[t, θ3]},
{x[t, θ2], y[t, θ2]},
{x[t, θ1], y[t, θ1]}
}, {t, Max[0, τ - 0.05], τ},
PlotStyle -> {{Opacity[0.5], Red}, {Opacity[0.5], Cyan}, {Opacity[0.5], Blue}}]
]}, {"t" -> Evaluate[τ]}}, Alignment -> Left]]],
{τ, 0.01, 2 π Sqrt[r/g], 0.01}]Fadenpendel, Stangenpendel, mathematisches Pendel, physikalisches Pendel, analytische exakte und explizite Lösung