Notizblock

Wenn wir auf kosmologischen Skalen ein rotverschobenes Objekt sehen können wir daraus unter anderem ablesen

1) wie viele Jahre lang sein Licht bis zu uns gereist ist
2) wie viele Lichtjahre es von uns entfernt war als es sein Licht aussandte
3) wie weit es bis jetzt wo wir das Licht empfangen gekommen ist
4) wie schnell das Objekt sich damals von uns entfernt hat
5) wie schnell es sich heute von uns entfernt


Die verwendeten kosmischen Parameter sind H0 = 67150 m/Mpc/sek; ΩR = 548e-5; ΩM = 317/1000; ΩΛ = 1-ΩR-ΩM; ΩK = 0
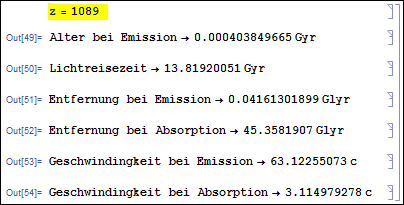
Damit ergibt sich ein Weltalter von 13.8196 Gyr. Die Plots gehen bis zu einer Rotverschiebung von z = 20:
________________________________________________________

Plot 1: Lichtreisezeit; x = z, y = t (in Gyr)



Das um den Faktor (20+1) rotverschobene Licht war 13.64 Mrd Jahre lang unterwegs.
________________________________________________________

Plot 2: Abstand damals; x = z, y = d (in Glyr)



Unser Testobjekt war als es sein Licht aussandte 1.7 Mrd Lj von uns entfernt.
________________________________________________________

Plot 3: Abstand heute; x = z, y = d (in Glyr)



Heute ist es bereits 35 Mrd Lj von uns entfernt (der maximale Partikelhorizont für z→∞ betrüge 46.386 Mrd Lj).
________________________________________________________

Plot 4: Geschwindigkeit damals; x = z, y = v (in c)



Die Rezessionsgeschwindigkeit des Objekts relativ zu uns betrug damals 6.35 fache Lichtgeschwindigkeit.
________________________________________________________

Plot 5: Geschwindigkeit heute; x = z, y = v (in c)



Heute beträgt die Rezessionsgeschwindigkeit unseres Objekts 2.46 c relativ zu uns.
________________________________________________________

Plot 6: zum Vergleich die Eigengeschwindigkeit im lokalen Minkowskiraum; x = z, y = v (in c)



Im lokalen nichtexpandierenden Raum würde die Lichtgeschwindigkeit auch bei z=∞ nicht überschritten.
________________________________________________________

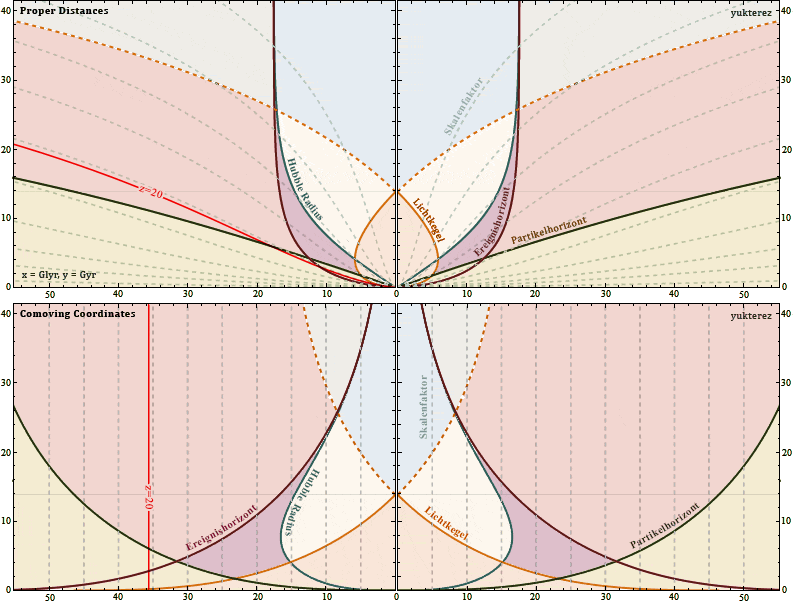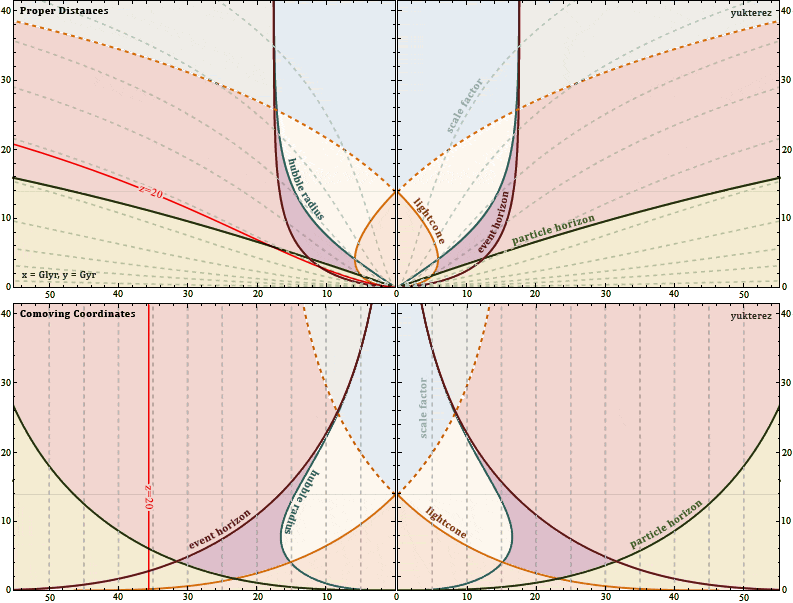
Die Trajektorie unseres Objekts (rot) in physikalischen und mitbewegten Koordinaten:


________________________________________________________

Das verwendete Modell ist ΛCDM/FLRW mit den Daten von Planck 2013. Wenn eine Kombination aus Eigenbewegung im lokalen Raum und Rezessionsgeschwindigkeit mit dem expandierenden Raum vorliegt werden beide Faktoren (z+1) miteinander multipliziert (die Eigengeschwindigkeit zum Zeitpunkt der Emission ist dann die Ausschlaggebende). Die Abweichung in der Rotverschiebung durch Eigenbewegung ist aber normalerweise vernachläßigbar klein (sie beträgt in etwa ±0.2%).

Wikipedia hat geschrieben:Currently, the objects with the highest known redshifts are galaxies and the objects producing gamma ray bursts. The highest confirmed spectroscopic redshift of a galaxy is that of UDFy-38135539 at a redshift of z = 8.6

Die heute bei uns eintreffende Hintergrundstrahlung hat allerdings eine Rotverschiebung von z = 1089.
Zu der Zeit gab es dort zwar noch keine voneinander unterscheidbaren Objekte wie Sterne oder Galaxien sondern nur mehr oder weniger homogene Ursuppe, aber nichtsdestotrotz hier die Zahlen für den wirklich allerhöchsten beobachtbaren Redshift:

Wenn man weiter nachrechnet stellt sich heraus dass sich alle Koordinaten mit einer Rotverschiebung von

z > 1.5855 zu dem Zeitpunkt als sie ihr Licht aussandten mit v > c von uns entfernten, und alle mit
z > 1.4855 heute mit einer Rezessionsgeschwindigkeit von v > c vor uns fliehen. Bei
z = 1.8963 ist das Objekt heute wieder genau so schnell wie damals (1.1572 c).

Davis & Lineweaver haben geschrieben:
Since their worldlines have always been beyond the Hubble sphere these objects were, are, and always have been, receding from us faster than the speed of light.

Achsen: x = Rotverschiebung z, y = Rezessionsgeschwindigkeit (Einheit: c)

Man sieht jetzt auch dass Objekte mit z < 1.8963 heute schneller sind als zum Zeitpunkt wo sie ihr Licht aussandten (die Expansionsrate hat sich seither nicht so stark verändert wie ihr Abstand), während Objekte mit z > 1.8963 inzwischen langsamer geworden sind (die Expansionsrate ist in der längeren Zeit wo das Licht unterwegs war stärker abgefallen als sich der Abstand des Objekts zu uns erhöht hat).

Da die Rezessionsgeschwindigkeit das Produkt aus Expansionsrate und Abstand ist und die Expansionsrate in Zukunft fast konstant bleiben wird beschleunigen die abgebremsten Objekte inzwischen wieder (auch wenn sie ihre ursprüngliche Geschwindigkeit noch nicht wiedererlangt haben), siehe auch den anderen Faden über die beschleunigte Expansion. Am Raum:Zeit-Plot ist der Übergang zur Beschleunigung übrigens dort wo die strichlierte Kurve (Skalenfaktor) anfängt sich nicht mehr nach oben sondern seitauswärts zu krümmen zu sehen (die Schubumkehr war ziemlich genau 8 Mrd Jahre nach dem Urknall, das ist in etwa bei z = 0.6).



Cosmological Redshift - Distance - Light Travel Time, Proper & Comoving: Calculations, Simon Tyran, Wien (Vienna)