Das ist die deutschsprachige Version. 
English version: click here.
Framework: Gravitationsgesetz nach Newton; Keywords: Abstandsquadrat, Rechnung, Differentialgleichung, Formel, Bewegungsgleichungen
1) Konstante DichteNeutonisches gravitatives Potential V einer auf die z=0-Ebene ausgerichteten Scheibe mit Masse M, Radius я und Flächendichte ρ=M/π/я²:
Polares und äquatoriales Potential mit r=0 als Funktion von z bzw. mit z=0 als Funktion von r:
Semianalytische Lösung als elliptisches Integral:
Schwerefeld der Scheibe:
Vektorkomponenten der Bewegungsgleichung:
Sitzt zusätzlich eine Kugel mit Masse Ḿ und Radius ʁ im Zentrum addieren sich die betreffenden Terme hinzu. Potential der Kugel:
Hier wird von einer durchlässigen Kugel mit konstanter Dichte ausgegangen. Funktion für die innere Restmasse:
Zusätzliche Komponenten des Beschleunigungsvektors in Anwesenheit der Kugel:
Die Umlaufgeschwindigkeit v ergibt sich über die Zentrifugalkraft:
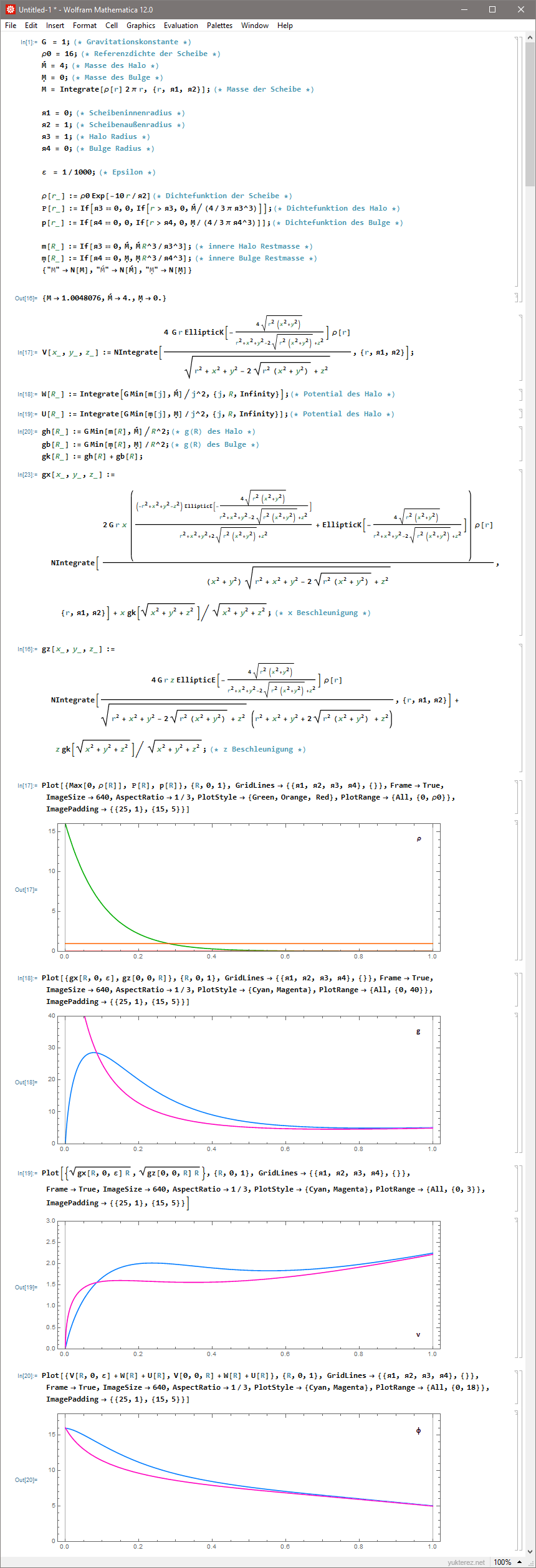
G ist die Gravitationskonstante. Benötigte Variablen:
Definitionen der benötigten Funktionen und elliptischen Integrale:
Für einen Annulus mit Innen- und Außenradius я1 und я2 wird eine Scheibe mit я=я1 von einer Scheibe mit я=я2 subtrahiert, bzw. wird statt von 0 bis я von я1 bis я2 integriert. Für einen Vergleich der semianalytischen Lösung mit einer Brute Force n-Body Simulation klick hier.⑴ Vergleich von Fallbeschleunigung g (oberer Plot), Umlaufgeschwindigkeit v (mittlerer Plot) und Potential Φ (unterer Plot); die grauen Kurven zeigen g, v und Φ im Feld einer Kugel mit Ḿ=ʁ=1, die blauen im Feld einer Scheibe mit M=я=1 bei R=x, y=z=0 und die violetten bei R=z, x=y=0. Die horizontale Achse bezeichnet den Abstand des Testpartikels vom Zentrum, R:
⑵ Plot für das kombinierte Feld eines Saturnoiden mit zentraler Kugel mit Ḿ=1, ʁ=я3=10 und Ring mit M=1, я1=15, я2=20:
⑶ Proberechnung für eine unendlich ausgedehnte Scheibe mit я=∞, ρ=1 (Lösung: g=2πGρ=konstant):
⑷ Neben der Scheibe ist g höher als über derselben, und bei einer Kugel oder Punktmasse in allen Richtungen gleich stark. M=1, R=2:
⑸ Zeile 1: Vektoren des Schwerefelds einer Scheibe mit M=1, я=20. Zeile 2: Konturen konstanter Schwere; links: y=0, rechts: z=0:
⑹ Feld einer annulären Scheibe mit M=1, я1=15, я2=20; (das Schalentheorem gilt wie man sieht nur bei Kugeln, nicht bei Scheiben):
⑺ Vektor- & Kontur-Plot mit einem Ring wie oben und zusätzlich einer Kugelmasse mit Ḿ=1 und ʁ=10 im Zentrum:
Ⅰ Geneigter Orbit um eine dünne Scheibe mit Masse M=1 und radius я=20 (für die Startbedingungen klick auf die Bilder):
Ⅱ Ein anderer geneigter Orbit um die gleiche Scheibe wie im oberen Beispiel:
Ⅲ Geschlossener polarer Orbit um eine Scheibe wie die obere:
Ⅳ Polarer Orbit um eine Kugel mit Ḿ=1, ʁ=я3=10 mit einem Ring mit M=1/2 und einem Innen/Außen-Radius von я1=15, я2=20:
Ⅴ Geschlossener polarer Orbit um einen Ringplaneten wie im oberen Beispiel:
Ⅵ Äquatorialer Kreisorbit, Kugel und Ring mit den gleichen Eigenschaften wie im vorigen Beispiel:
Ⅶ Inklinierter Orbit, Kugel : Ḿ=1/2, ʁ=я3=10; Ring: M=1, я1=15, я2=20:
Ⅷ Gravitationstunnel durch einen saturnoiden und durchlässigen Planeten mit Ḿ=1, ʁ=10 und einem Ring mit M=1/2:
Ⅸ Gravitationstunnel durch einen Ring mit M=1:
Ⅹ Gravitationstunnel mit Inklination, Ring wie im oberen Beispiel:
Ⅺ Sternförmiger Orbit um einen Ring bzw. Annulus mit M=1, я1=15, я2=20:
Ⅻ Orbit innerhalb einer durchlässigen Scheibe mit M=1, я=20 (z=0+ε, z"=0), Anfangsgeschwindigkeit v⊥=√(GM/я):
Display, Spalten [1|2|3|4]→[Position|Geschwindigkeit|Beschleunigung|Massenverteilung]
Video in Full HD: klick. Für die Anzeige des gesamten Codes klick hier, und für ein anderes Beispiel hier.
Anmerkungen: - Im Integral für V kann sofern die Dichtefunktion isotrop ist aufgrund der Scheibensymmetrie von ∫{...}d[θ=0..2π] auf 2∫{...}d[θ=0..π] umgestellt werden um die Rechenzeit am Computer zu beschleunigen. Bei konstanter Dichte empfiehlt sich die semianalytische Lösung, da diese um Größenordnungen schneller ist als das numerische Integral.
- Plot ⑴ zeigt dass die Umlaufgeschwindigkeit innerhalb einer homogenen Scheibe mit steigendem Radius stärker steigt als das in einer homogenen Kugel der Fall wäre. Die blaue v-Kurve für R=r, z=0 zeigt die benötigte Kreisgeschwindigkeit in der äquatorialen Ebene, während die violette v-Kurve für R=z, r=0 die benötigte Geschwindigkeit für z"=0 zeigt (aufgrund der Asymmetrie sind bei zu geringer Höhe über dem Zentrum der Scheibe keine geschlossenen polaren Orbits möglich).
- Plot ⑵ zeigt dass g an den Rändern der annulären Scheibe divergiert; die Scheibe wird sozusagen zu einem Ring zusammengedrückt. Das führt unter anderem dazu dass protoplanetare Scheiben sich zu Planeten verdichten können. Die Divergenz exakt am Rand lässt sich verhindern indem ein Mindestabstand in der Größe des mittleren Abstands der Teilchen aus denen sich die Scheibe zusammensetzt zur selben eingehalten wird, damit der Testpartikel nicht auf die unendlich dünne Fläche mit zwar endlicher Flächendichte, aber unendlicher Volumendichte knallt. Um Orbits in der rein äquatorialen Ebene die in die Scheibe hineinreichen zu studieren wird z'=z"=0, z=0+ε gesetzt wobei ε beispielsweise bei einer Galaxie sinnvollerweise der mittlere Abstand der Sterne untereinander wäre, oder beim Saturnring der Radius der Steinchen aus denen sich der Ring zusammensetzt.
- Die zweite Zeile in Plot ⑸ zeichnet die Flächen konstanter Gravitation entlang derer der Meeresspiegel verliefe sofern die Scheibe mit Wasser bedeckt wäre und die Masse des Wassers im Vergleich zur Scheibe gering wäre.
