
Ableitung der Position p nach der Zeit t in abstandstreuen Koordinaten, Beschleunigung:
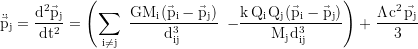
mit der Distanz d zwischen den jeweiligen Körpern i und j:
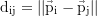
und der Coulomb-Konstante k:
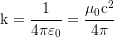
Wenn die Expansion des Universums berücksichtigt wird ist die kosmologische Konstante
Schwerpunkt des Systems:
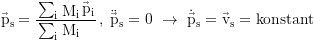
Zwei Körper bleiben stationär zueinander wenn das Ladung/Masse-Verhältnis
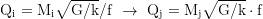
wobei f eine beliebige Zahl ist. Mit berücksichtigter Expansion ist das Gleichgewicht beim Abstand/Masse-Verhältnis
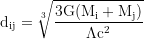
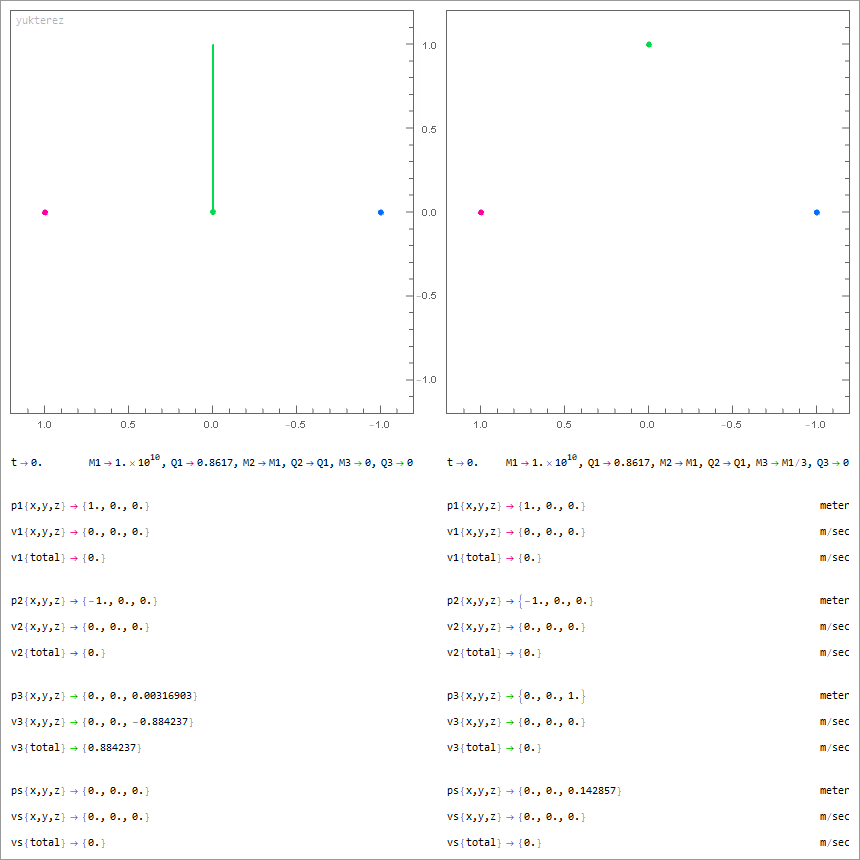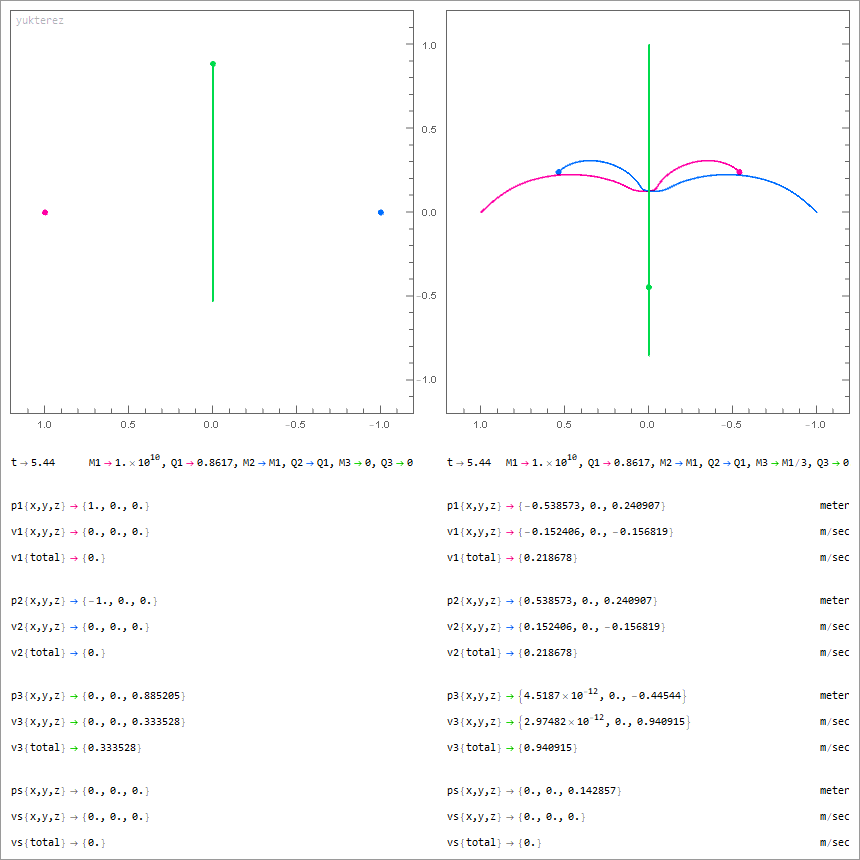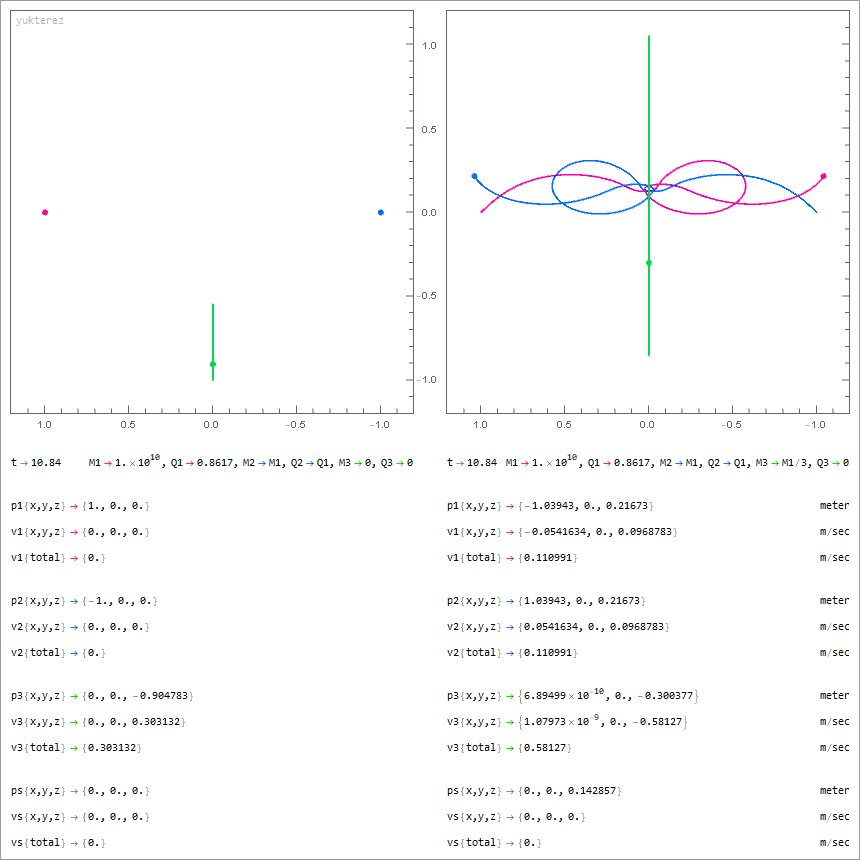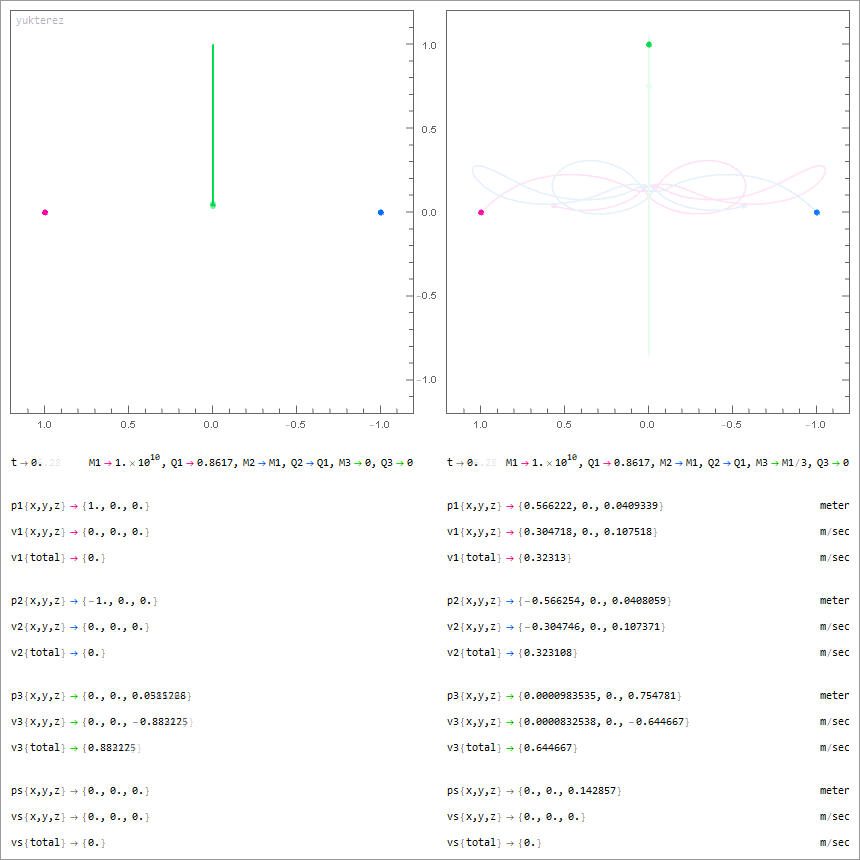
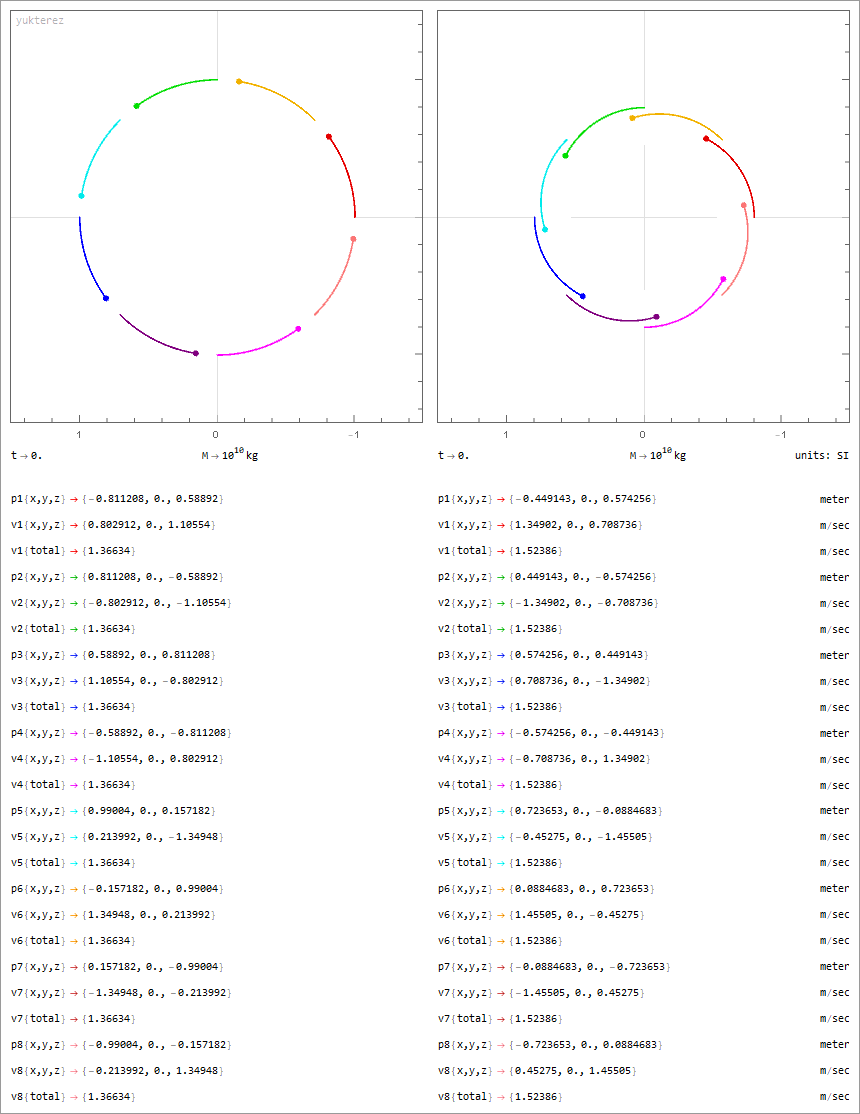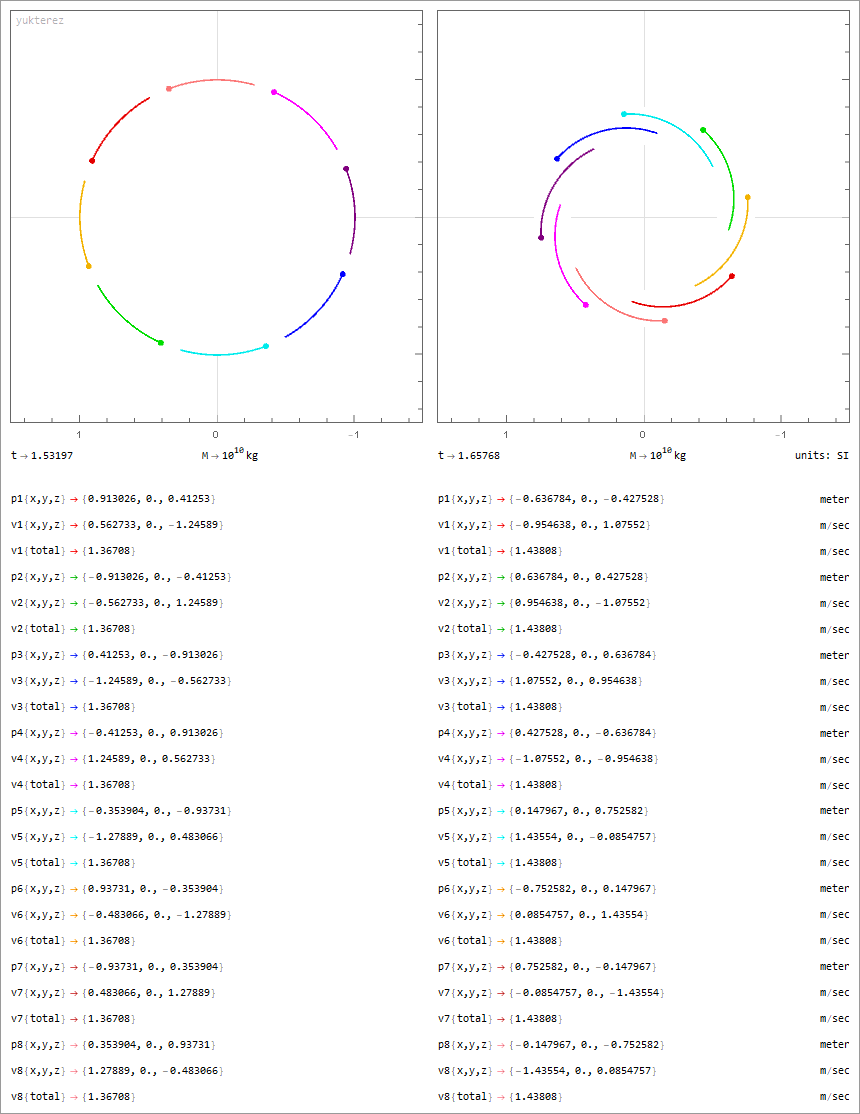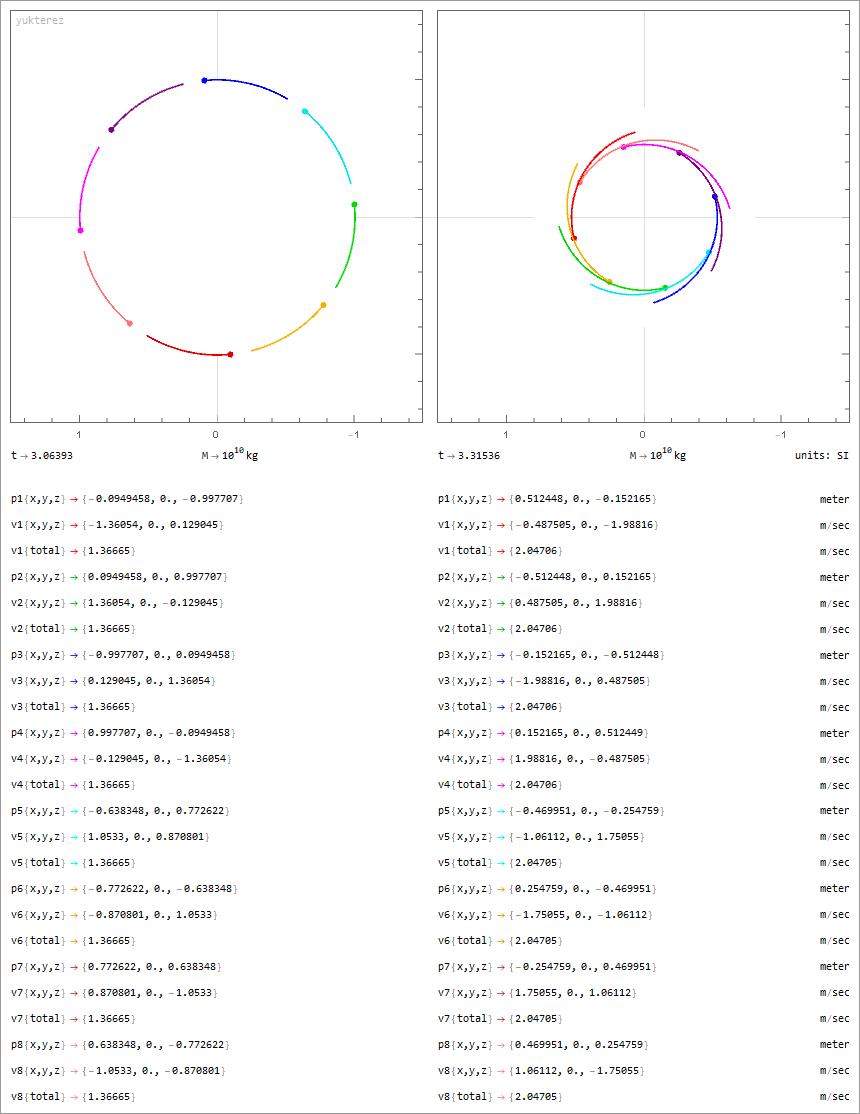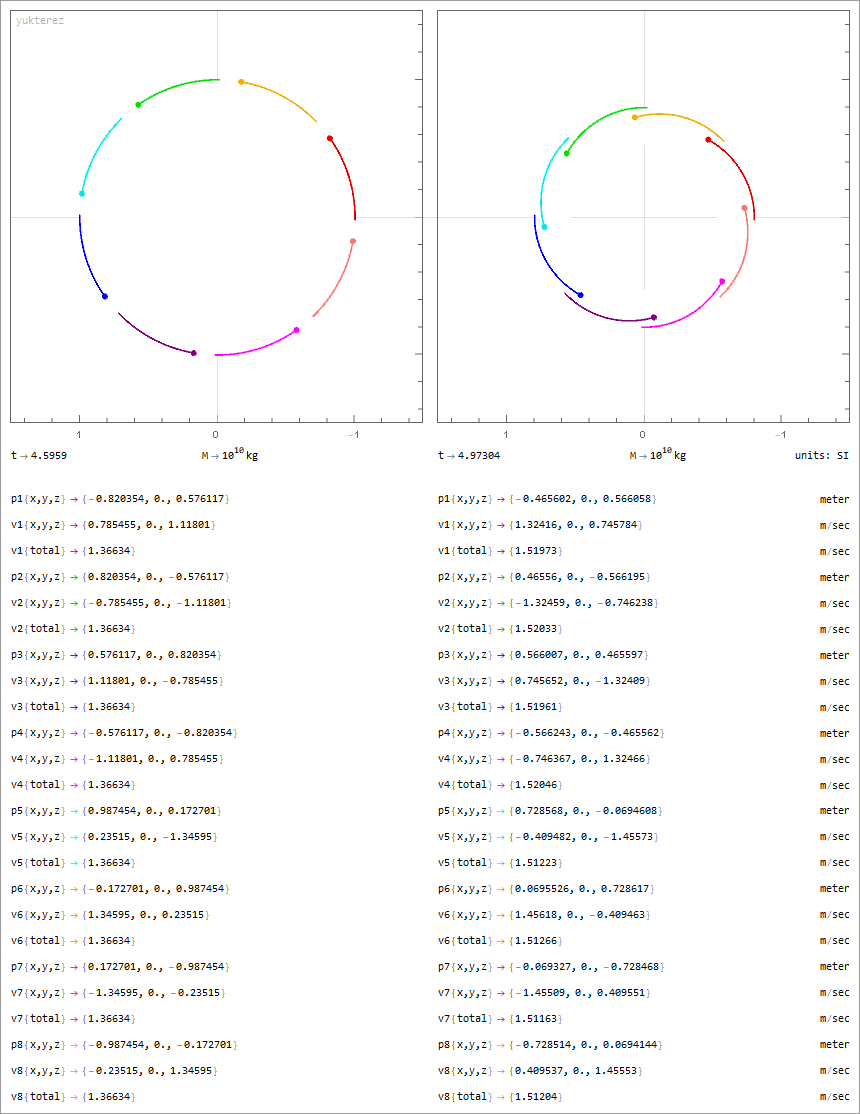
Notation: Newton. Variablen: M=Masse, Q=Ladung, p=Position, v=Geschwindigkeit, G=Gravitationskonstante, ε₀=Feldkonstante, Λ=Lambda.

3 Körper, links: symmetrische Startpositionen, rechts: asymmetrisch; t: Sekunden


2 mit Q=M√(G/k) geladene und 1 neutraler Körper (grün); links: masseloser Testpartikel, rechts: massiver neutraler Drittkörper


6 Körper, zufällig gewählte Startbedingungen; links: Seitenansicht, rechts: Draufsicht, Schweiflänge: 100 sek



8 Körper mit jeweils 10¹⁰ kg, geschlossene Orbits in symmetrischer Anordnung:


Diskussion: hier und hier







