Das ist die deutschsprachige Version. 
For the english version see here. 
Kritischer Wert für die dunkle Energie ΩΛ in einem geschlossenen Universum; ein geringerer Wert führt zu einem Big Crunch, der exakte Wert zu einem Stillstand und ein höherer Wert sorgt dafür dass der Hubbleparameter H nie 0 wird und letztendlich auf einen konstanten Wert zukonvergiert, also eine beschleunigte Expansion:
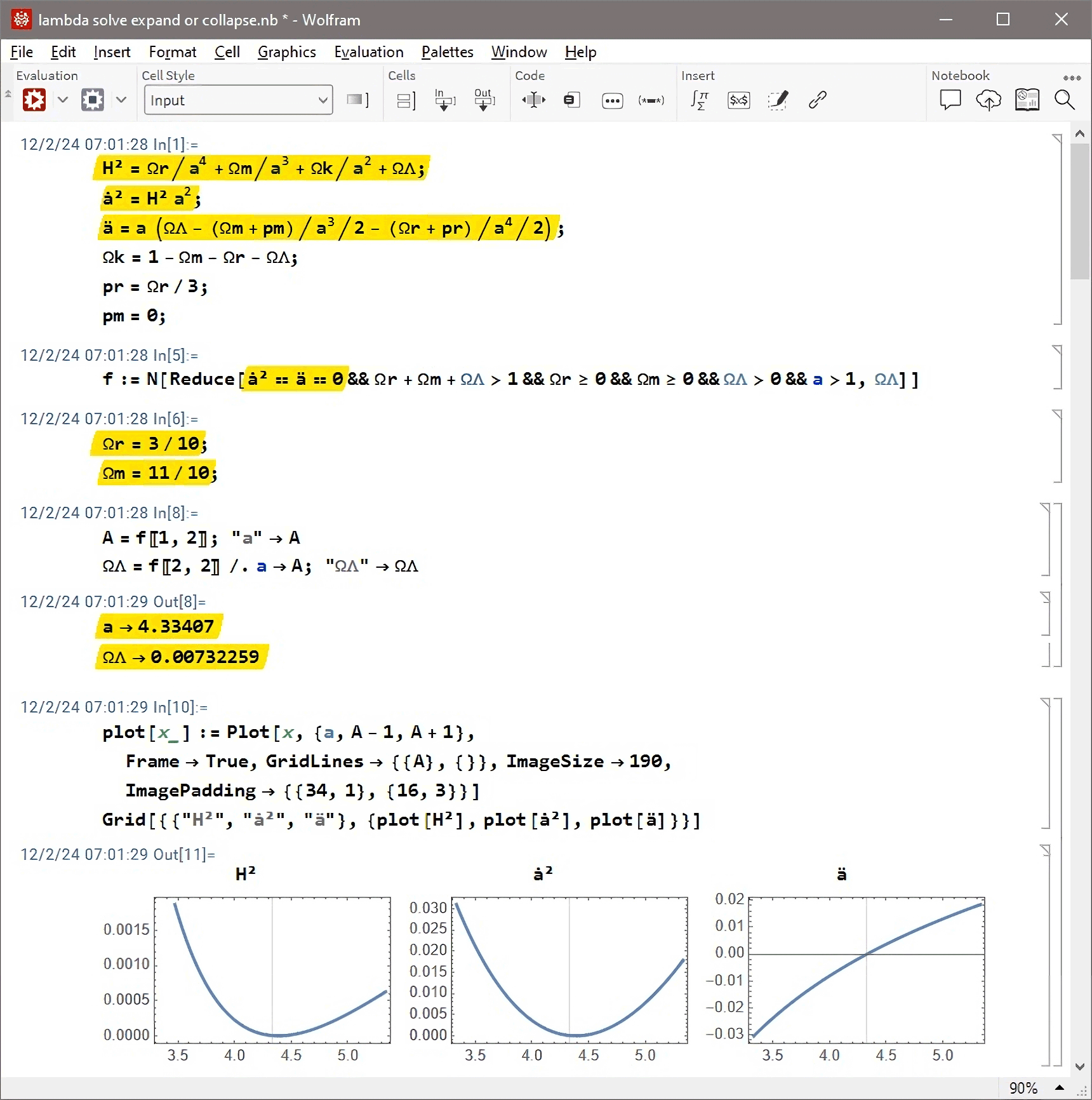
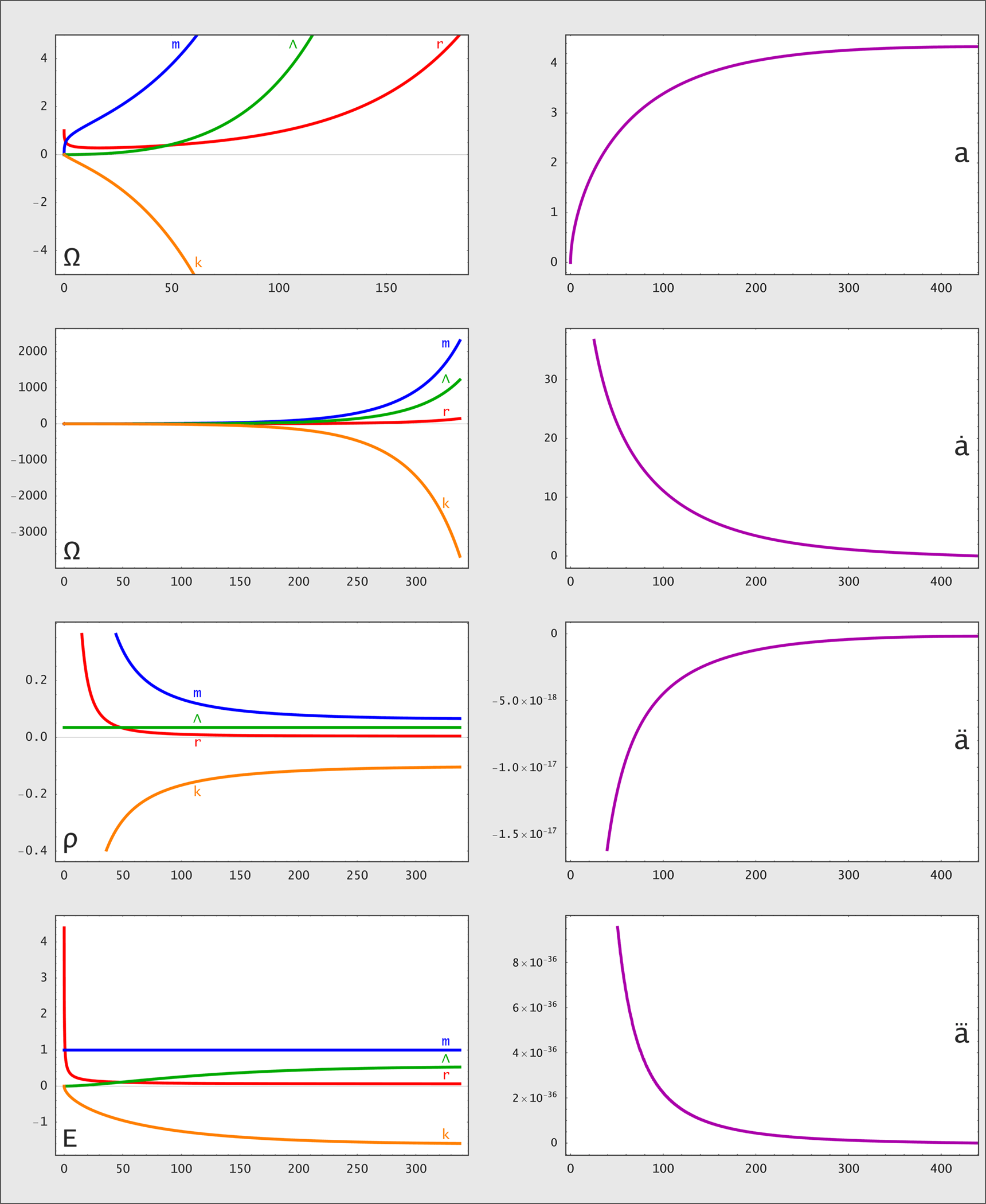
Anwendungsbeispiel: Bei In[1] wird der normalisierte Hubbleparameter H und die erste und zweite Zeitableitung (ȧ und ä) des normalisierten Skalenfaktors a sowie die Zusammenhänge zwischen Druck, Dichte und Krümmung definiert. Bei In[5] wird die Geschwindigkeit und Beschleunigung der Expansion auf 0 gesetzt um nach dem Grenzwert zwischen Expansion und Kontraktion aufzulösen. Bei In[6] werden die gewünschten Werte für die Materie Ωm und die Strahlung Ωr festgelegt. Bei In/Out[8] wird das für den Grenzfall benötigte ΩΛ und der Skalenfaktor bei dem das unstabile Gleichgewicht eintritt ausgegeben, was zur Probe bei Out[11] nochmal geplottet wird. Die Plotwerte nach der vertikalen Hilfslinie gehören zu solchen a Werten die zu keinem vorhersehbaren Zeitpunkt t erreicht werden da beim maximalen a von hier a=4.33407 sowohl H=0 als auch dH/dt=0, also ein unstabiles Gleichgewicht erreicht wird:
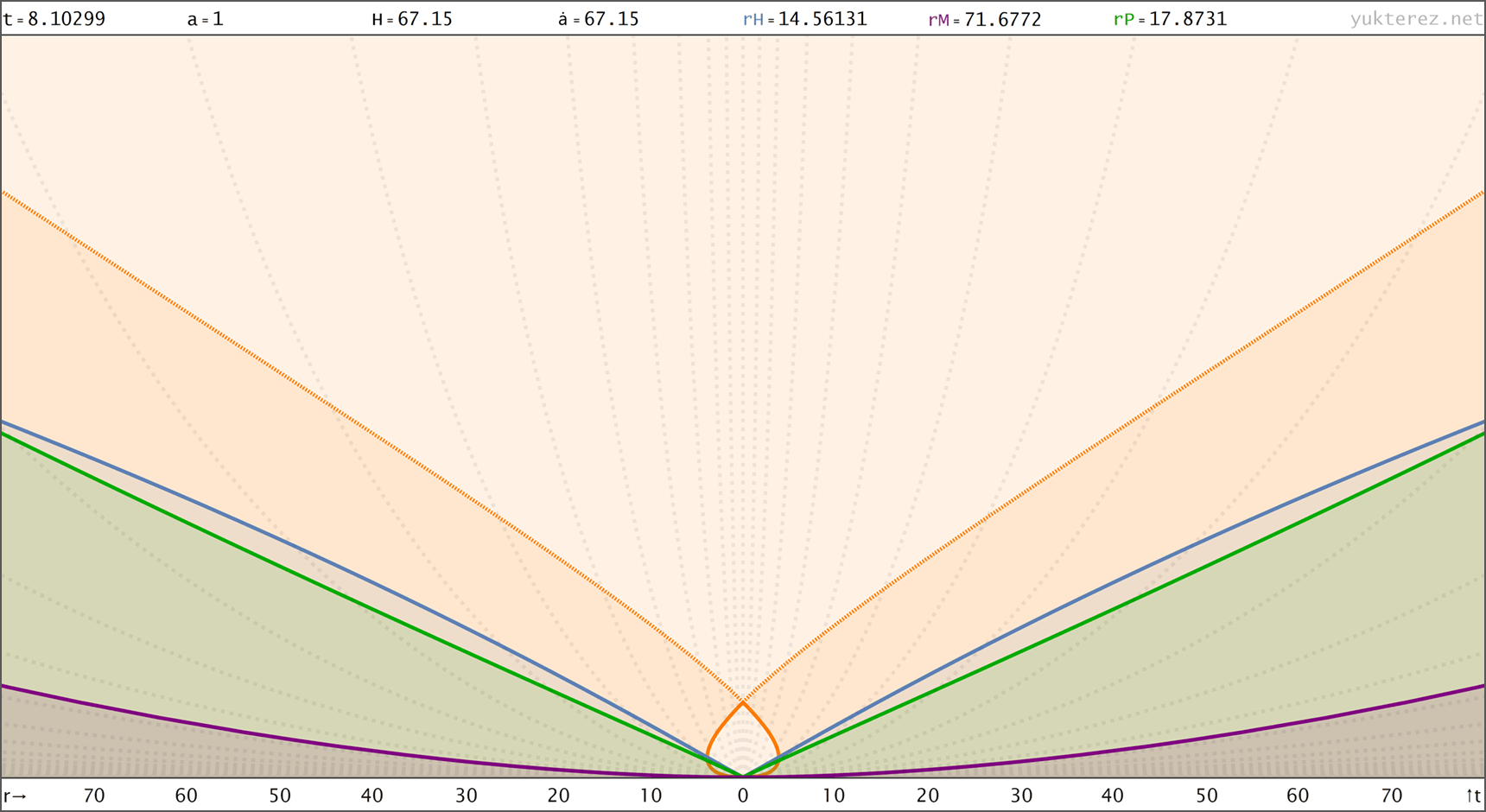
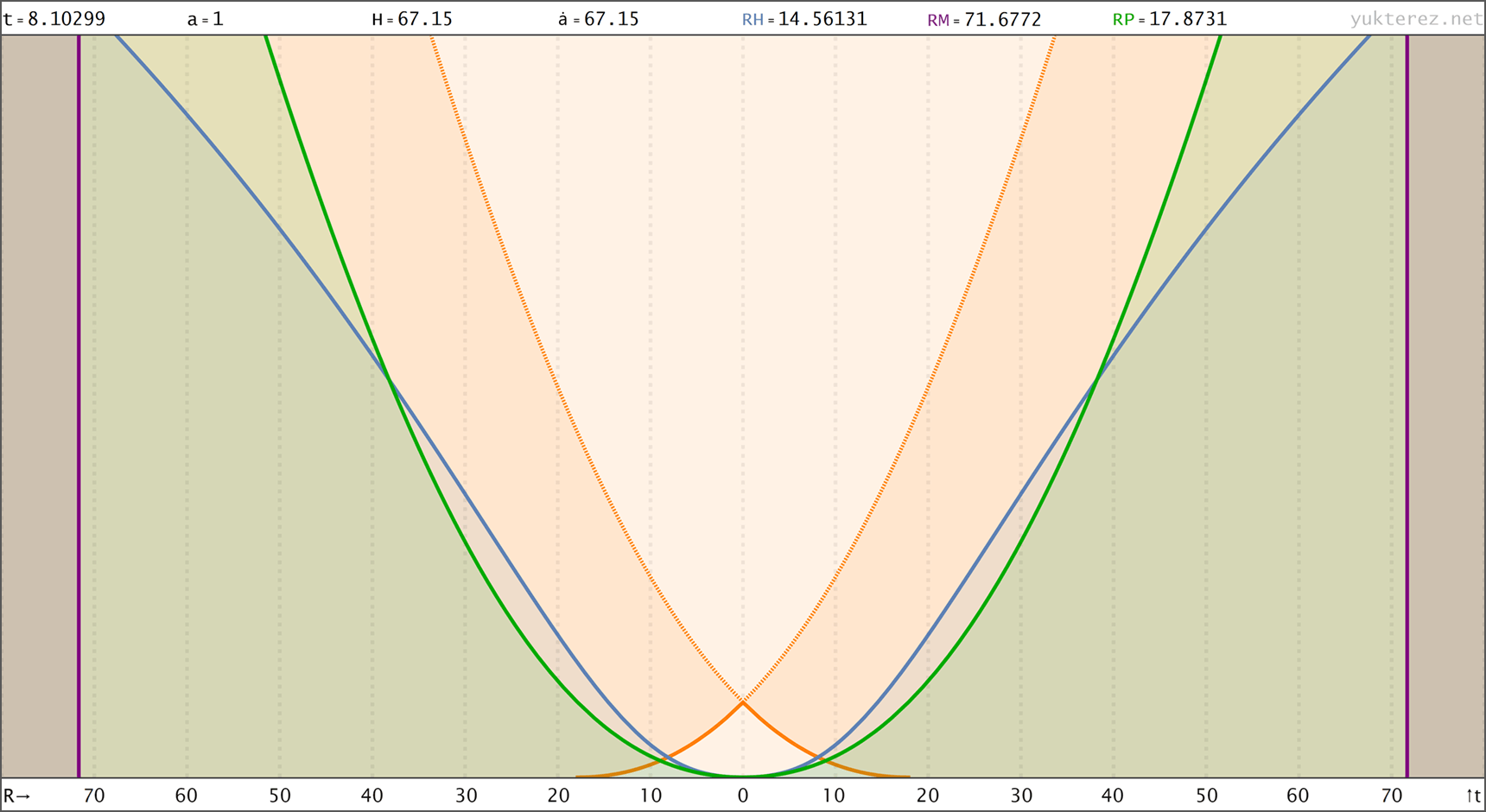
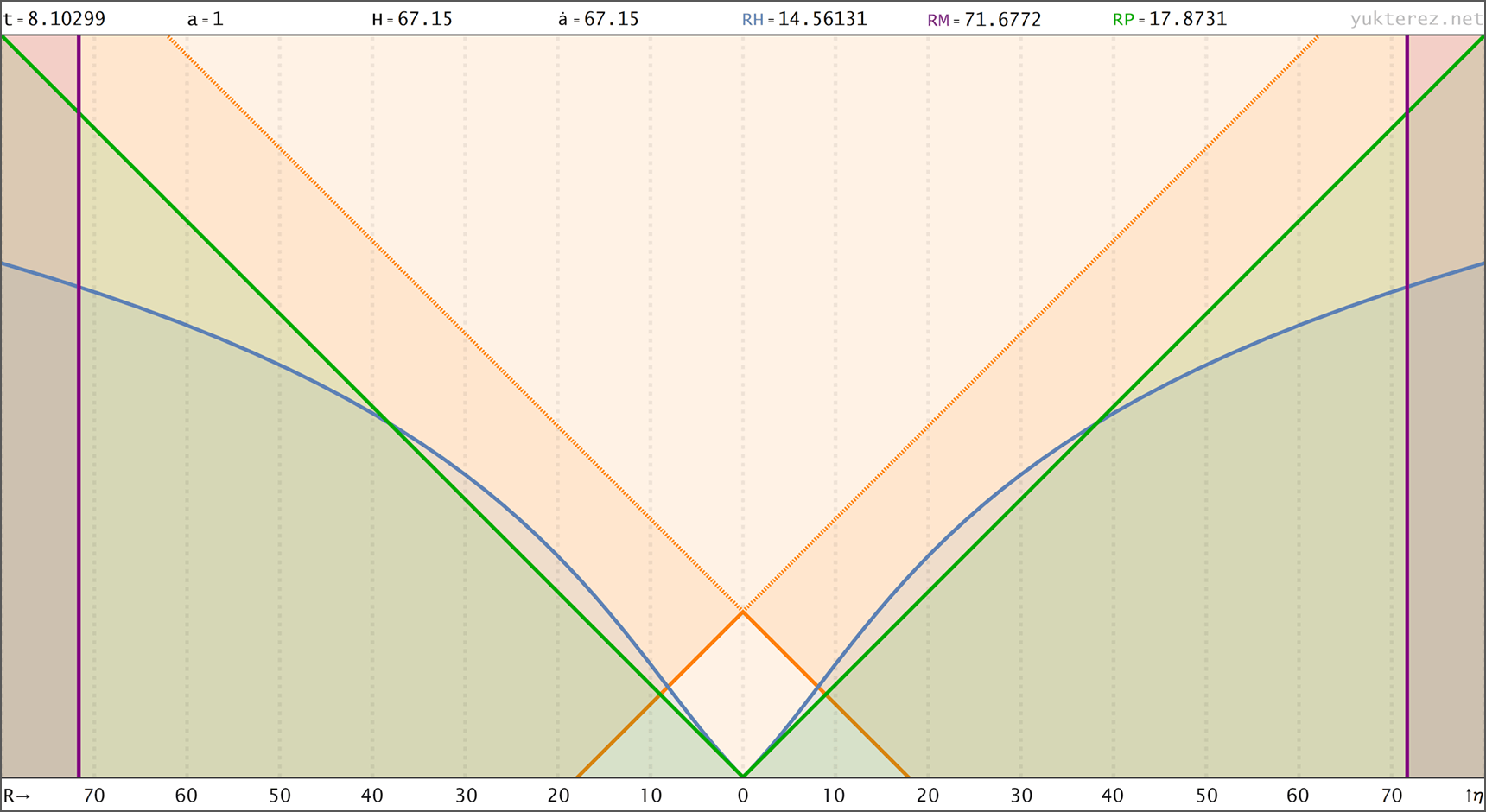
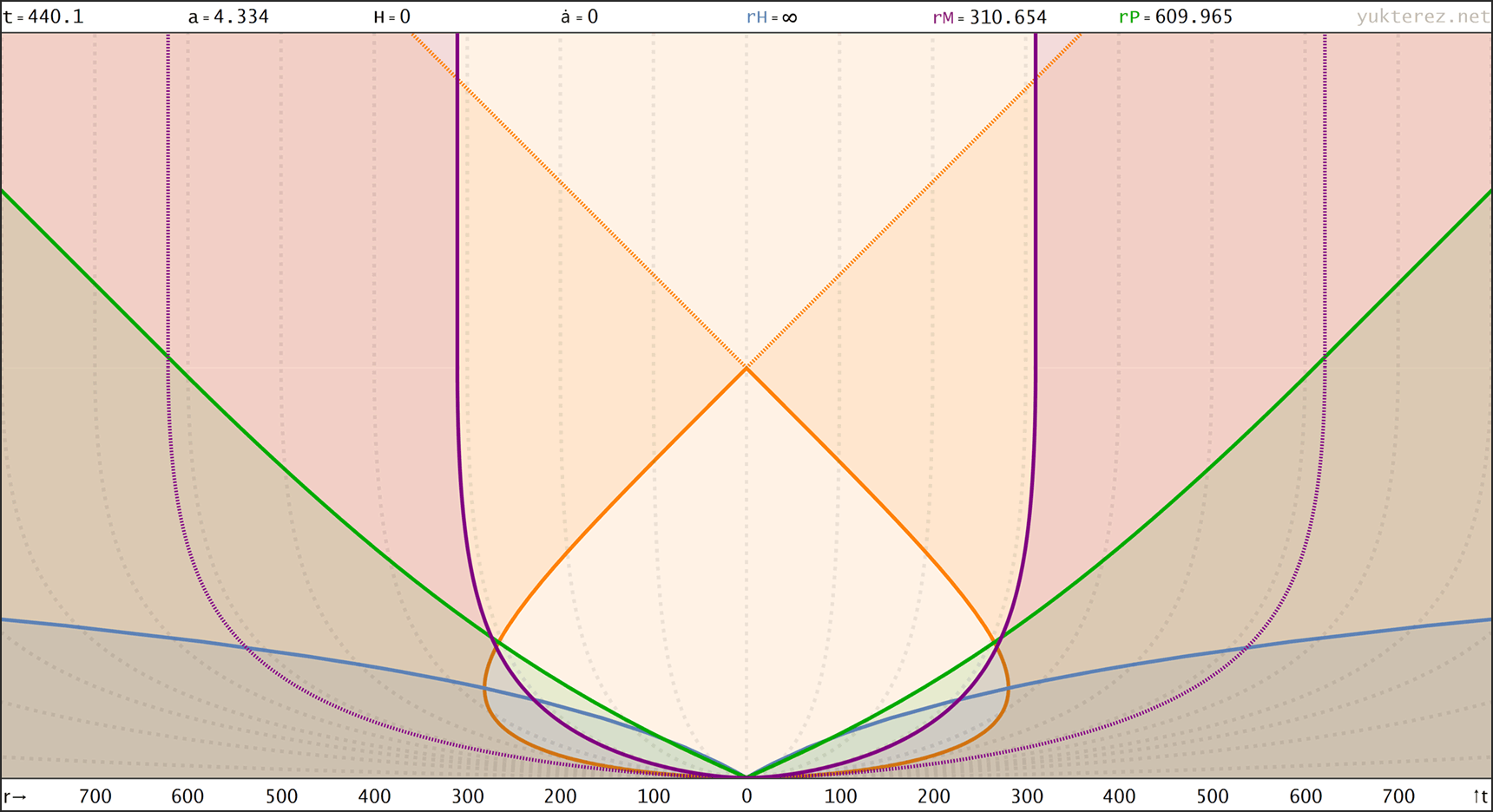
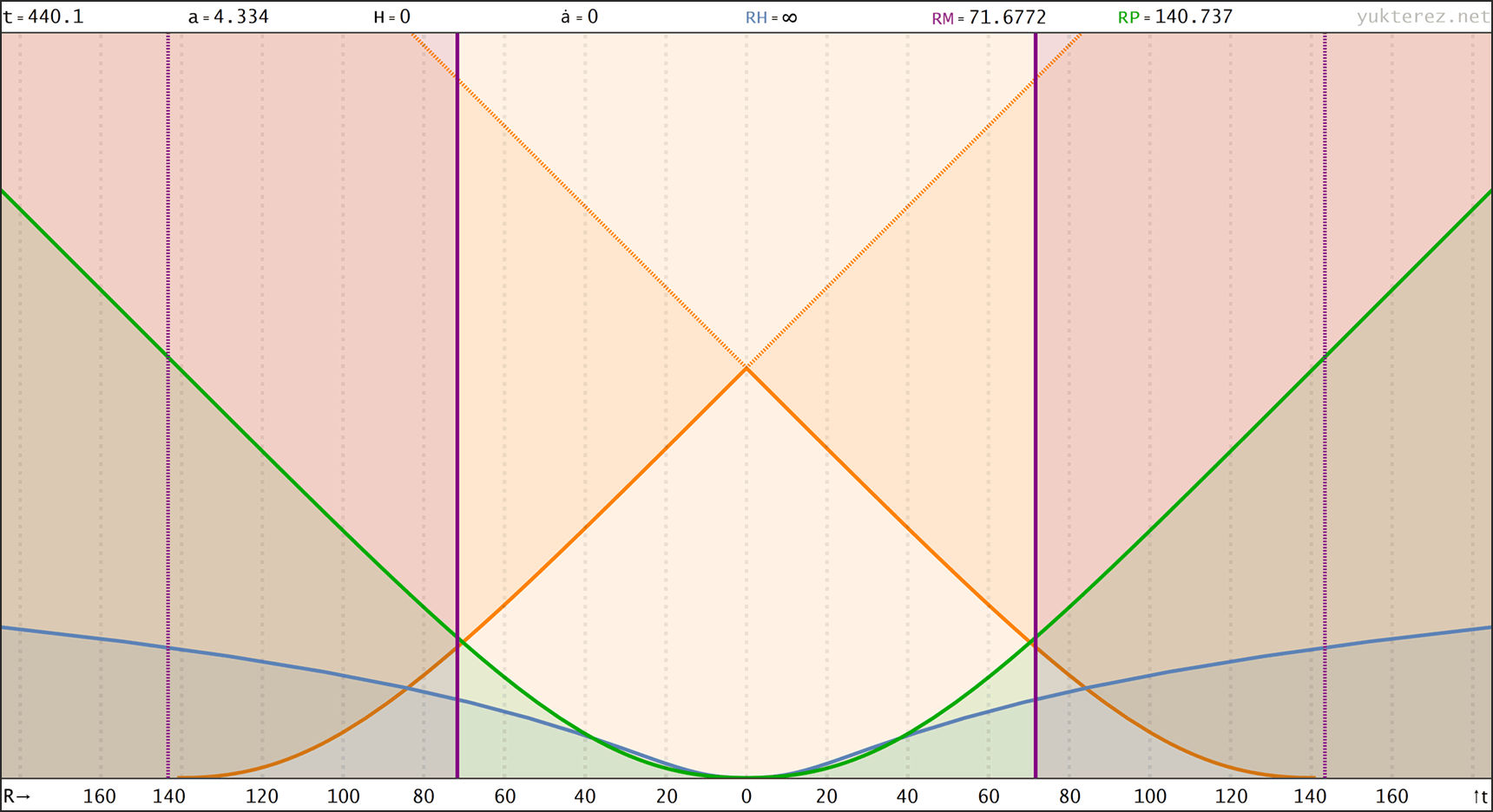
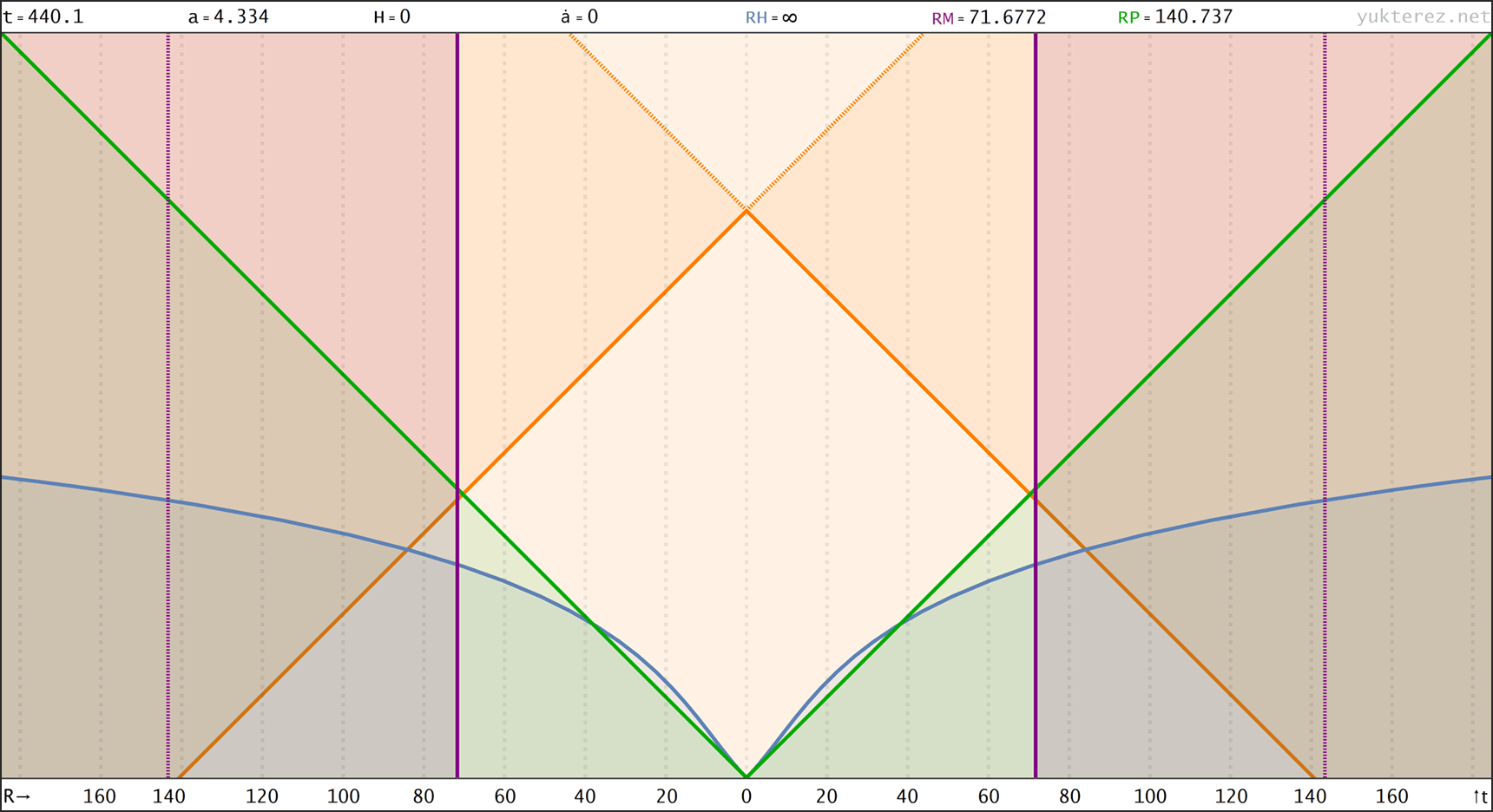
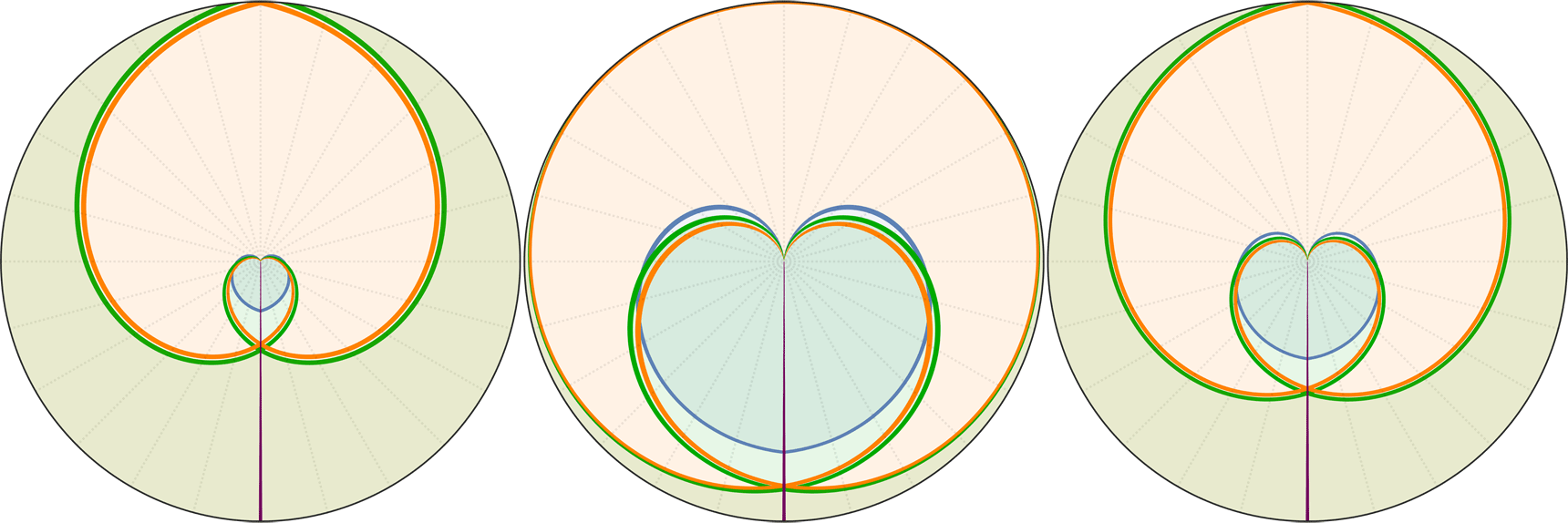
Raumzeitdiagamme des oberen Universums in Proper Distance r(t), Comoving Distance R(t) & nach Conformal Time R(η) Koordinaten. rH: Hubble Radius (blau), rE: Ereignishorizont (keiner), rP: Partikelhorizont (grün), orange Kurve: Lichtkegel, graue Kurven: mitbewegte Weltlinien, R=r/a:
Die Metrik in radiusgetreuen und umfanggetreuen Koordinaten findet sich in dieser Liste. Da hier oben die radialen Abstände eingezeichnet sind wurden Erstere verwendet. Raumzeitdiagrammcode:
Code: Alles auswählen
(* | Solver for the critical value of ΩΛ in a closed universe || yukterez.net | *)
Ωk = 1-Ωm-Ωr-ΩΛ;
pr = Ωr/3;
pm = 0;
H² = Ωr/a^4+Ωm/a^3+Ωk/a^2+ΩΛ;
ȧ² = H² a^2;
ä = a (ΩΛ-(Ωm+pm)/a^3/2-(Ωr+pr)/a^4/2);
Ωr = 3/10;
Ωm = 11/10;
f = N[Reduce[ȧ²==ä==0 && Ωr+Ωm+ΩΛ>1 && Ωr>=0 && Ωm>=0 && ΩΛ>0 && a>1, ΩΛ]]
A = f[[1,2]]
ΩΛ = f[[2,2]]/.a->A
plot[x_]:=Plot[x, {a, A-1, A+1}, Frame -> True, GridLines -> {{A}, {}}]
"H²"->plot[H²]
"ȧ²"->plot[ȧ²]
"ä"->plot[ä]
Quit[]Anwendungsbeispiel: Bei In[1] wird der normalisierte Hubbleparameter H und die erste und zweite Zeitableitung (ȧ und ä) des normalisierten Skalenfaktors a sowie die Zusammenhänge zwischen Druck, Dichte und Krümmung definiert. Bei In[5] wird die Geschwindigkeit und Beschleunigung der Expansion auf 0 gesetzt um nach dem Grenzwert zwischen Expansion und Kontraktion aufzulösen. Bei In[6] werden die gewünschten Werte für die Materie Ωm und die Strahlung Ωr festgelegt. Bei In/Out[8] wird das für den Grenzfall benötigte ΩΛ und der Skalenfaktor bei dem das unstabile Gleichgewicht eintritt ausgegeben, was zur Probe bei Out[11] nochmal geplottet wird. Die Plotwerte nach der vertikalen Hilfslinie gehören zu solchen a Werten die zu keinem vorhersehbaren Zeitpunkt t erreicht werden da beim maximalen a von hier a=4.33407 sowohl H=0 als auch dH/dt=0, also ein unstabiles Gleichgewicht erreicht wird:
Raumzeitdiagamme des oberen Universums in Proper Distance r(t), Comoving Distance R(t) & nach Conformal Time R(η) Koordinaten. rH: Hubble Radius (blau), rE: Ereignishorizont (keiner), rP: Partikelhorizont (grün), orange Kurve: Lichtkegel, graue Kurven: mitbewegte Weltlinien, R=r/a:
↑ proper, r(t) ◉ ↓ comoving, R(t)
↑ comoving, R(t) ◉ ↓ conformal, R(η)
↑ t = 8.1 Gyr, a = 1 ◉ ↓ t = 440.1 Gyr, a = 4.334
↑ proper, r(t) ◉ ↓ comoving, R(t)
↑ comoving, R(t) ◉ ↓ conformal, R(η)
Die Metrik in radiusgetreuen und umfanggetreuen Koordinaten findet sich in dieser Liste. Da hier oben die radialen Abstände eingezeichnet sind wurden Erstere verwendet. Raumzeitdiagrammcode:
Code: Alles auswählen
(* | Evolution of a closed FLRW Universe that reaches an unstable equilibrium | *)
set = {"GlobalAdaptive", "MaxErrorIncreases"->100,
Method->"GaussKronrodRule"}; (* Integration Rule *)
if[F_] := If[ΩΛ<=0, Nothing, If[ΩK>0, Nothing, F]] (* Event Horizon Check *)
n = 100; (* Recursion Depth *)
int[f_, {x_, xmin_, xmax_}] := (* Integral *)
NIntegrate[f, {x, xmin, xmax},
Method->set, MaxRecursion->n, WorkingPrecision->wp];
wp = MachinePrecision; (* Working Precision *)
im = 200; (* Image Size *)
ηmax = 800; pmax = 800; (* Plot Range *)
amax = 4.334070910330731109143449787268; (* Maximal Scale Factor *)
tmax = 440 Gyr; (* Integration Limit *)
c = 299792458 m/sek; (* Lightspeed *)
G = 667384*^-16 m^3 kg^-1 sek^-2; (* Newton Constant *)
Gyr = 10^7*36525*24*3600 sek; (* Billion Years *)
Glyr = Gyr*c; (* Billion Lightyears *)
Mpc = 30856775777948584200000 m; (* Megaparsec *)
ρc[H_] := 3H^2/8/π/G; (* Critical Density *)
ρΛ = ρc[H0] ΩΛ; (* Dark Energy Density *)
kg = m = sek = 1; (* SI Units *)
ΩR = 3/10; (* Radiation Proportion including Neutrinos *)
ΩM = 11/10; (* Matter Proportion including Dark Matter *)
ΩΛ = 0.0073225878457081148392542953; (* Dark Energy Proportion *)
ΩT = ΩR+ΩM+ΩΛ; (* Total Density over Critical Density *)
ΩK = 1-ΩT; (* Curvature Density *)
H0 = 67150 m/Mpc/sek; (* Hubble Constant *)
H[a_] := H0 Sqrt[ΩR/a^4+ΩM/a^3+ΩK/a^2+ΩΛ] (* Hubble Parameter *)
sol = Quiet[NDSolve[{A'[t]/A[t] == H[A[t]], A[0] == 1*^-15},
A, {t, 0, tmax},
MaxSteps->∞, WorkingPrecision->wp]];
â[t_] := Evaluate[(A[t]/.sol)[[1]]]; (* Scale Factor a by Time t *)
a[t_] := If[t<tmax, â[t], amax]; (* Scale Factor a by Time t *)
т[a_] := int[1/A/H[A], {A, 0, a}]; (* Time t by Scale Factor a *)
rP[t_] := a[t] int[c/a[т], {т, 0, t}]; (* Proper Particle Horizon by t *)
rp[a_] := a int[c/A^2/H[A], {A, 0, a}]; (* Proper Particle Horizon by a *)
RP[t_] := int[c/a[т], {т, 0, t}]; (* Comoving Particle Horizon by t *)
Rp[a_] := int[c/A^2/H[A], {A, 0, a}]; (* Comoving Particle Horizon by a *)
rE[t_] := if[a[t] int[c/a[т], {т, t, ∞}]]; (* Proper Event Horizon by t *)
re[a_] := if[a int[c/A^2/H[A], {A, a, ∞}]]; (* Proper Event Horizon by a *)
RE[t_] := if[int[c/a[т], {т, t, ∞}]]; (* Comoving Event Horizon by t *)
Rε[a_] := if[int[c/A^2/H[A], {A, a, ∞}]]; (* Comoving Event Horizon by a *)
rL[t0_, t_] := a[t] int[c/a[т], {т, t, t0}]; (* Proper Light Cone by t *)
rl[a0_, a_] := a int[c/A^2/H[A], {A, a, a0}]; (* Proper Light Cone by a *)
RL[t0_, t_] := int[c/a[т], {т, t, t0}]; (* Comoving Light Cone by t *)
Rl[a0_, a_] := int[c/A^2/H[A], {A, a, a0}]; (* Comoving Light Cone by a *)
rH[t_] := c/H[a[t]]; (* Proper Hubble Radius by t *)
rh[a_] := c/H[a]; (* Proper Hubble Radius by a *)
RH[t_] := c/H[a[t]]/a[t]; (* Comoving Hubble Radius by t *)
Rh[a_] := c/H[a]/a; (* Comoving Hubble Radius by a *)
ã[η_] := Quiet[FindRoot[Rp[Ã]/Glyr-η, (* Scale Factor a by Conformal Time η *)
{Ã, 0.00001}, WorkingPrecision->wp, MaxIterations->1000][[1, 2]]];
ā = Quiet[Interpolation[Join[{{0, 0}},
ParallelTable[{((Sin[η π/ηmax-π/2]+1) ηmax/2),
ã[((Sin[η π/ηmax-π/2]+1) ηmax/2)]}, {η, ηmax/im, ηmax, ηmax/im}]]]];
Ť[η_] := Quiet[FindRoot[RP[τ Gyr]/Glyr-η, (* t by η *)
{τ, 1}, WorkingPrecision->wp, MaxIterations->1000][[1, 2]]]
(* ţ = Quiet[Interpolation[Join[{0, 0},
ParallelTable[{((Sin[η π/ηmax-π/2]+1) ηmax/2),
Ť[((Sin[η π/ηmax-π/2]+1) ηmax/2)]}, {η, ηmax/im, ηmax, ηmax/im}]]]]; *)
rpN = Rp[1]/Glyr;
t0 = Re[t/.FindRoot[a[t]-1, {t, 10 Gyr}]]; ti = t Gyr; τi = τ Gyr;
"t0"->t0/Gyr "Gyr" (* Current Time *)
"PROPER DISTANCES, f(t)"
pt = Quiet[Plot[Evaluate[
{rH[τi]/Glyr, rP[τi]/Glyr, rE[τi]/Glyr}],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot1[t_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[Evaluate[
{rL[ti, τi]/Glyr, -rL[ti, τi]/Glyr}],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], pt]], 90 Degree]}}]];
Do[Print[plot1[t]], {t, {tmax/Gyr}}]
plot2 = Rasterize[Grid[{{Rotate[Quiet[Plot[Evaluate[
Join[{0}, Table[1/amax a[τ Gyr] n^4/250, {n, 4, 55, 1}]]],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"COMOVING DISTANCES, f(t)"
ct = Quiet[Plot[Evaluate[
{rH[τi]/(a[τi]Glyr), rP[τi]/(a[τi]Glyr), rE[τi]/(a[τi]Glyr)}],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot3[t_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[Evaluate[
{rL[ti, τi]/(a[τi]Glyr), -rL[ti, τi]/(a[τi]Glyr)}],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], ct]], 90 Degree]}}]];
Do[Print[plot3[t]], {t, {tmax/Gyr}}]
plot4 = Rasterize[Grid[{{Rotate[Quiet[Plot[Evaluate[
Join[{0}, Table[n, {n, 100, pmax, 100}]]],
{τ, 0, pmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, pmax}, {0, pmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]
"COMOVING DISTANCES, f(η)"
cη = Quiet[Plot[Evaluate[
{Rh[ā[Ct]]/Glyr, Ct, Rε[ā[Ct]]/Glyr}],
{Ct, 0, ηmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, pmax}},
PlotStyle->{{Thickness[0.005]},
{Darker[Green], Thickness[0.005]}, {Purple, Thickness[0.005]}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}]];
plot9[η_] := Rasterize[Grid[{{Rotate[Quiet[Show[Plot[Evaluate[
{η-Ct, Ct-η}], {Ct, 0, ηmax},
Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, pmax}},
PlotStyle->{{Orange, Thickness[0.005]}, {{Orange, Thickness[0.005]}, Dashed}},
ImageSize->im, Filling->Top, FillingStyle->Opacity[0.1], ImagePadding->1,
GridLines->{{}, {}}], cη]], 90 Degree]}}]];
Do[Print[plot9[η]], {η, {RP[tmax]/Glyr}}]
plot10 = Rasterize[Grid[{{Rotate[Quiet[Plot[Evaluate[
Join[{0}, Table[n, {n, 100, pmax, 100}]]],
{Ct, 0, ηmax}, Frame->True, AspectRatio->1,
FrameTicks->None, PlotRange->{{0, ηmax}, {0, pmax}},
PlotStyle->Table[{Dashing->Large, Thickness[0.005],
Gray}, {n, 1, 100}], ImageSize->im, ImagePadding->1]], 90 Degree]}}]]