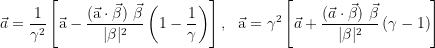Seite 1 von 1
Relativistic Acceleration
Verfasst: Mi 23. Jun 2021, 03:51
von Yukterez
This is the english version.
Eine deutschspachige Version findet sich
hier Index:
constant force |
constant coordinate acceleration |
constant power , discussion (autotranslate from german):
click here
Relativistic Acceleration
Verfasst: Mi 23. Jun 2021, 03:53
von Yukterez
CONSTANT FORCE
The velocity v is derived over the gammafactor γ
and the relativistic momentum p
where the force F, rest mass m and proper acceleration a
are connected with the differential of momentum p over coordinate time t. With that and F=constant we get
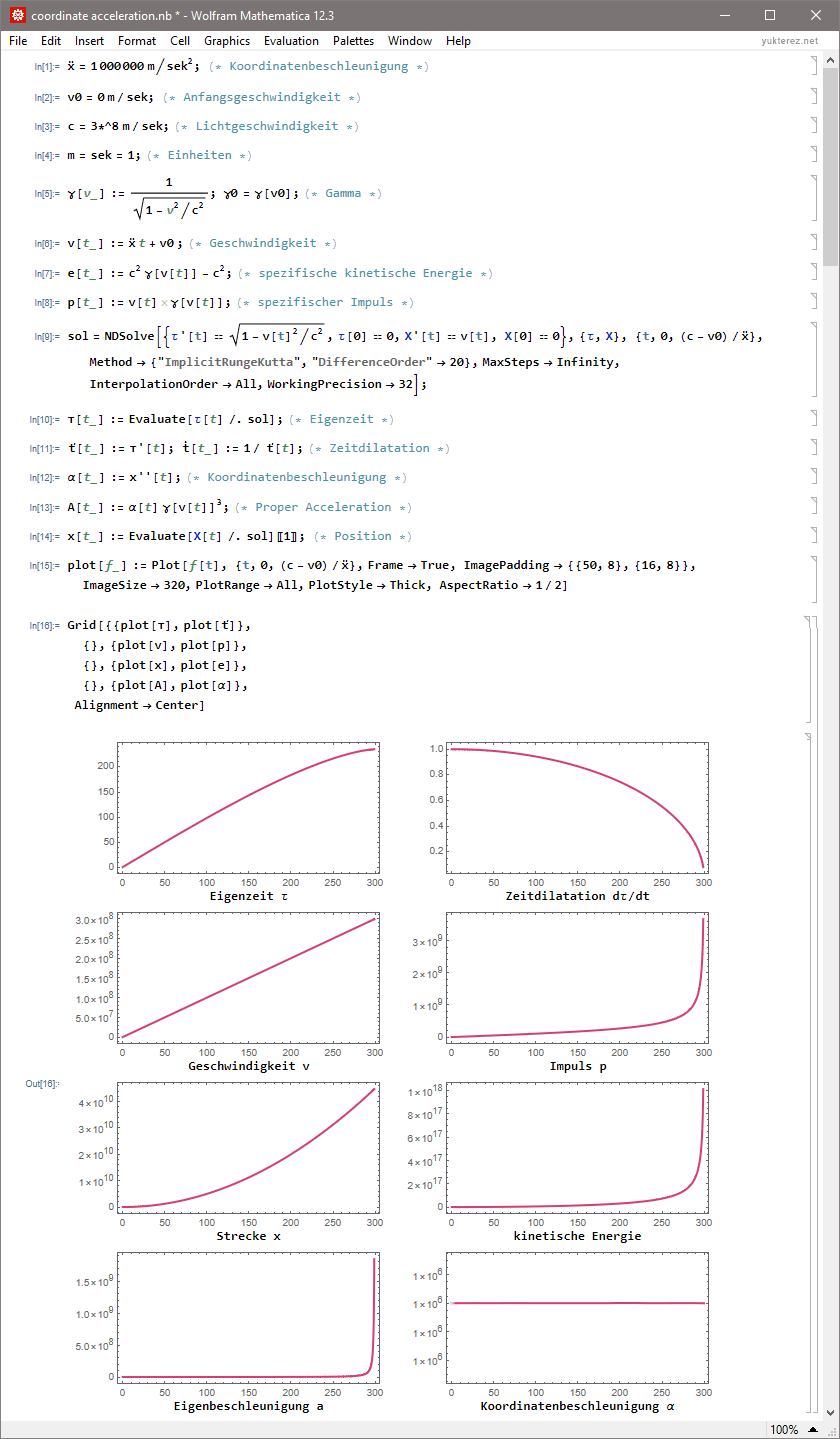
Plot with coordinate time t as x-axis (SI-units, momentum and energy as specific quantities per kg rest mass):
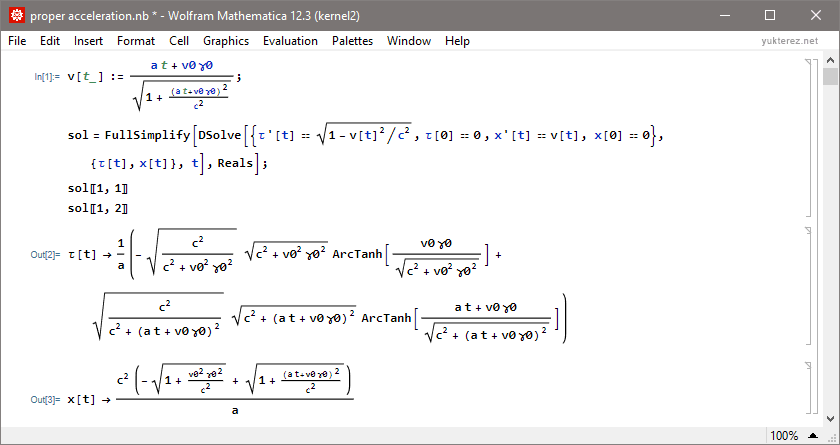
Analytical solutions for proper time τ and distance x:
Code:
Code: Alles auswählen
(* Eigenbeschleunigung, Methode 1 *) Code: Alles auswählen
(* Eigenbeschleunigung, Methode 2 *) Code: Alles auswählen
(* Eigenbeschleunigung, Methode 3 *) For a side by side comparison of the 3 different ways to do it
click here
Relativistic Acceleration
Verfasst: Mi 23. Jun 2021, 03:57
von Yukterez
CONSTANT COORDINATE ACCELERATION
With α=dv/dt=d²x/dt²=a/γ³=constant the equation for v is simply
With constant coordinate acceleration the speed of light would be reached when
Plot with coordinate time t as x-axis (SI-units, momentum and energy as specific quantities per kg rest mass):
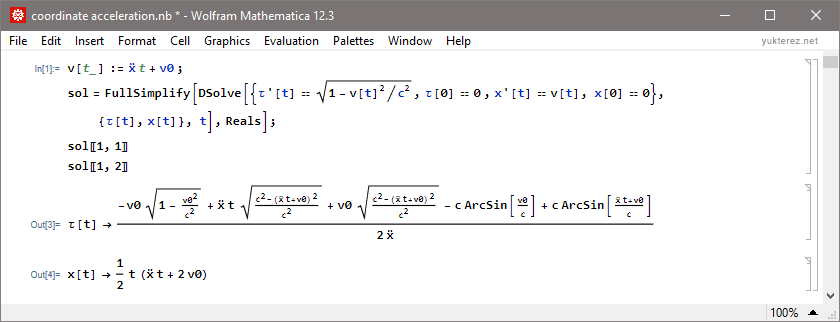
Analytical solutions for proper time τ and distance x:
Code:
Code: Alles auswählen
(* konstante Koordinatenbeschleunigung ẍ *)
Relativistic Acceleration
Verfasst: Mi 23. Jun 2021, 04:03
von Yukterez
CONSTANT POWER
With constant power L the energy mc²γ inreases linearly with t. The initial energy plus the applied work equals the new energy
where W is the applied work
If we solve for v we get
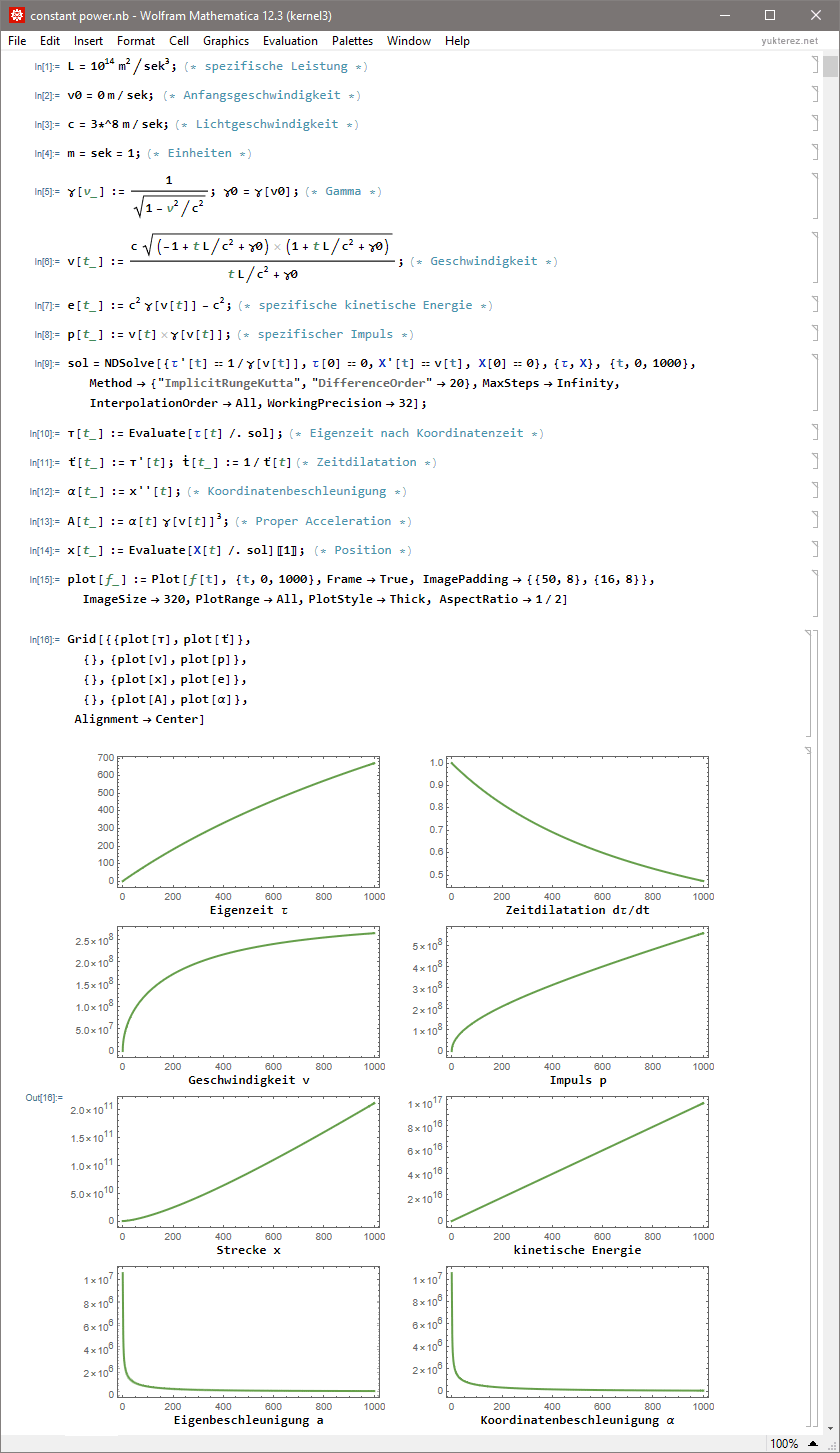
Plot with coordinate time t as x-axis (SI-units, momentum and energy as specific quantities per kg rest mass):
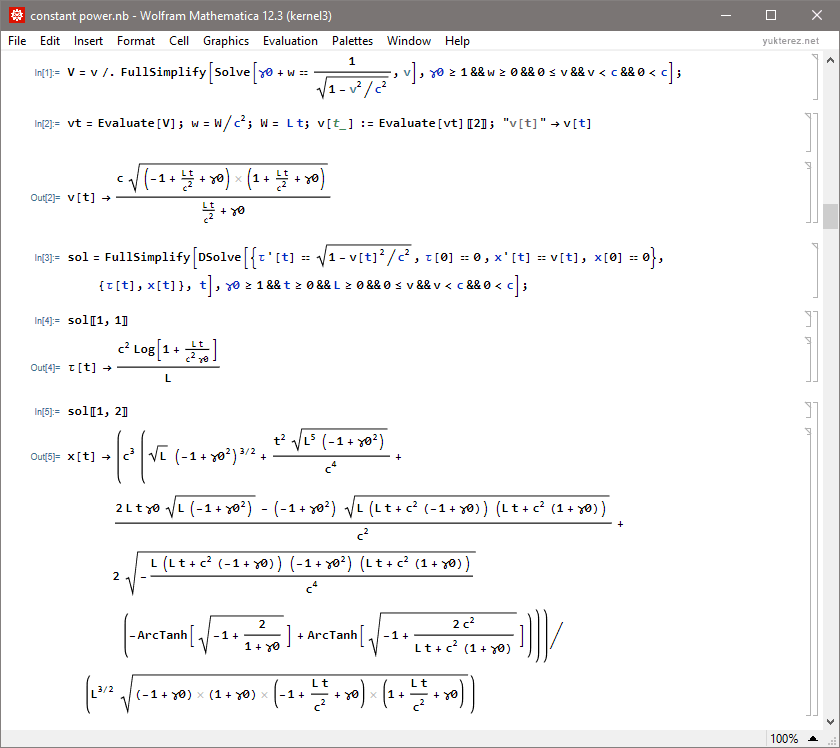
Analytical solutions for proper time τ and distance x:
Code:
Code: Alles auswählen
(* konstante Leistung *)
Relativistic Acceleration
Verfasst: Mi 12. Feb 2025, 20:43
von Yukterez
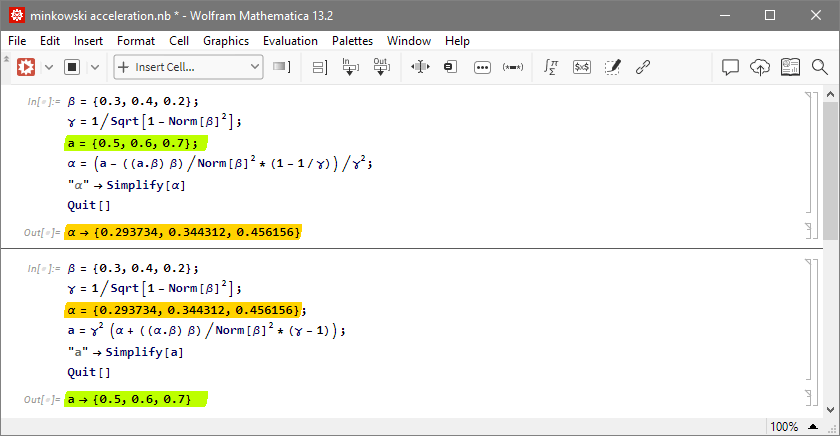
Vector notation: α is the coordinate acceleration of the accelerated observer in the unaccelerated frame, a is the proper acceleration of the accelerated observer in his own frame, v=βc is their relative velocity at the moment when they fly past each other:
Code:
Code: Alles auswählen
β={vx/c,vy/c,vz/c};Code: Alles auswählen
β={vx/c,vy/c,vz/c};Application in the context of the Schwarzschild metric:
physics.stackexchange.com/a/842494

 This is the english version.
This is the english version.  Eine deutschspachige Version findet sich hier
Eine deutschspachige Version findet sich hier