View from inside a Black Hole
Verfasst: Di 7. Jul 2020, 04:01


 This is the english version
This is the english version  Deutsche Version: klick
Deutsche Version: klick  This is a subchapter of Kerr Newman Metric and Relativistic Raytracer
This is a subchapter of Kerr Newman Metric and Relativistic Raytracer
Index:
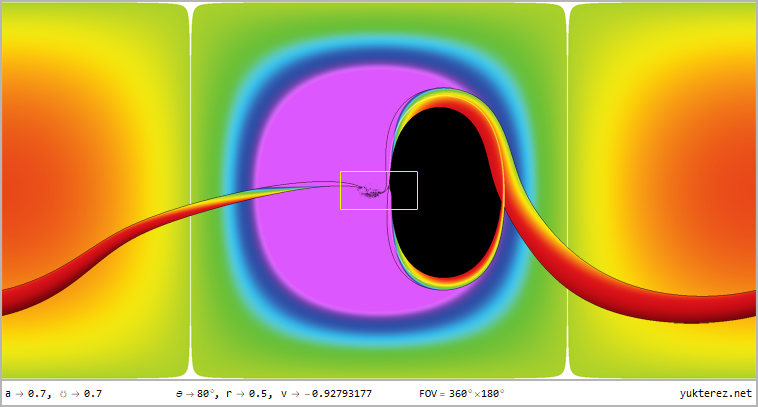
- Free faller, θ=80°, r={12, 4, r₊, r₋, 0.5} -|- ZAMO, θ=80°, r={12, 4, r₊+Δr, r₋-Δr, 0.5}

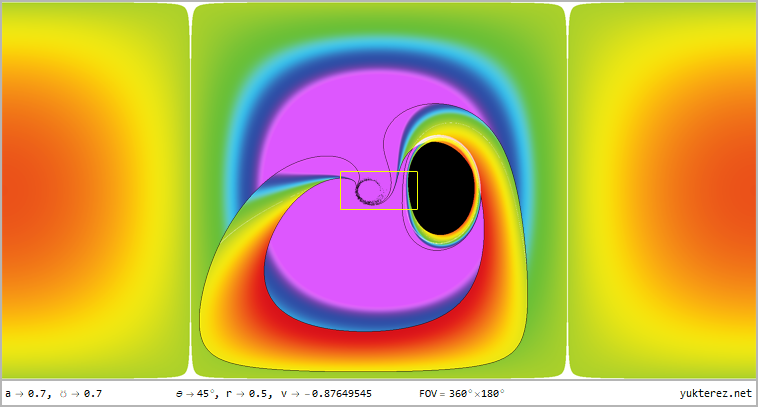
- Free faller, θ=45°, r={12, 4, r₊, r₋, 0.5} -|- ZAMO, θ=45°, r={12, 4, r₊+Δr, r₋-Δr, 0.5}
- Free faller, θ=10°, r={12, 4, r₊, r₋, 0.5} -|- ZAMO, θ=10°, r={12, 4, r₊+Δr, r₋-Δr, 0.5}
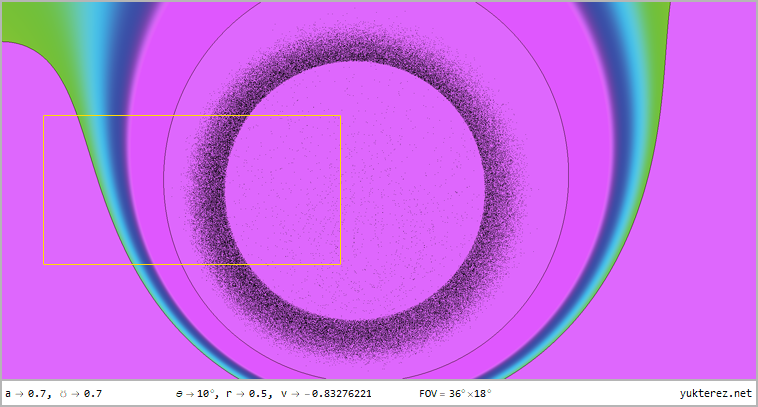
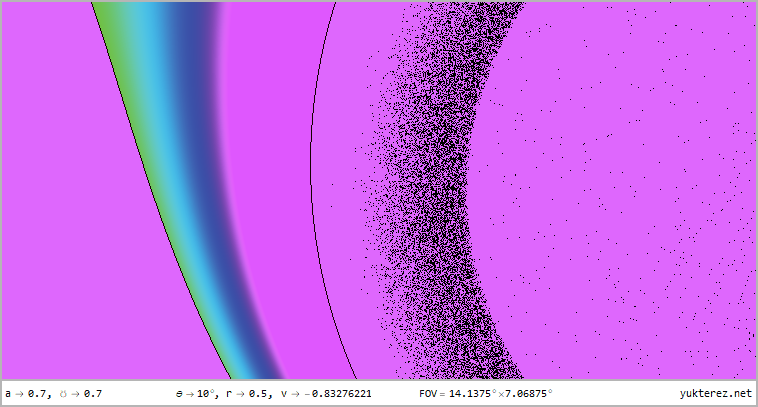
- Extras: zoom -|- undistorted view -|- technical details

Intro:


This thread shows the perspective of an observer that falls freely from infinity (with the negative escape velocity) into a
rotating black hole with spin a=0.7 and electric charge ℧=0.7, and compares it to the perspective of an observer in a radially
stationary LNRF at the same position. The black hole has an accretion disk rotating with the local circular orbit velocity, an
inner disk radius rᵢ=ISCO=1.63678 and outer disk radius rₐ=7; the raytraced images consist of 4 parts:

The first part shows the black hole with an accretion disk, and the second one without. In the third part a hollow shell with
a world map pattern is hovering slightly outside of the outer event horizon at 1.0001r₊ and corotates with the local frame
dragging velocity, see left for a cartesian x,y,z and right for a pseudospherical r,θ,φ projection:

In the cartesian representation it is shown that the singularity is actually a ring with the physical radius R=a, while in the
pseudospherical representation it is depicted at r=0. The relation of the cartesian radius R and angle Θ to the pseudospherical
coordinates r,θ,φ is R=√(r²+a² Sin[θ]), Θ=ArcCos[(r Cos[θ])/√(r²+a² Sin[θ]²)], Φ=φ. A freefaller from infinity (E=1) has a
constant θ in BL coordinates and also constant φ in Raindrop coordinates (but in both coordinates no constant Θ). The fourth
part shows the frequency shift of the background sky and the disk, color code in the range from fe/f0=0..2 (white for fe/f0=1):

In the ZAMO perspective the observer is not at the horizons, but slightly above the outer and below the inner horizon where the
escape/freefall-velocity (and therefore the local velocity relative to a raindrop) is v=0.9999c. Profile of the accretion disc's
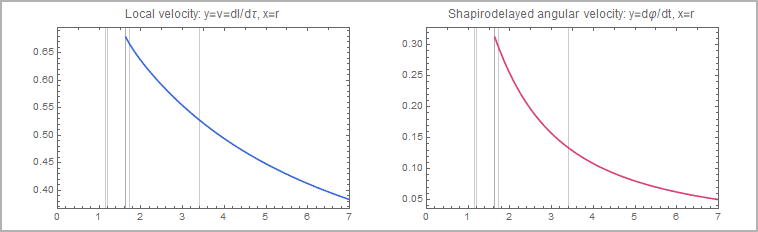
rotation: local circular orbit velocity relative to a ZAMO and shapiro delayed angular velocity as a funktion of r (the disc spins
counterclockwise with its left side toward the observer):
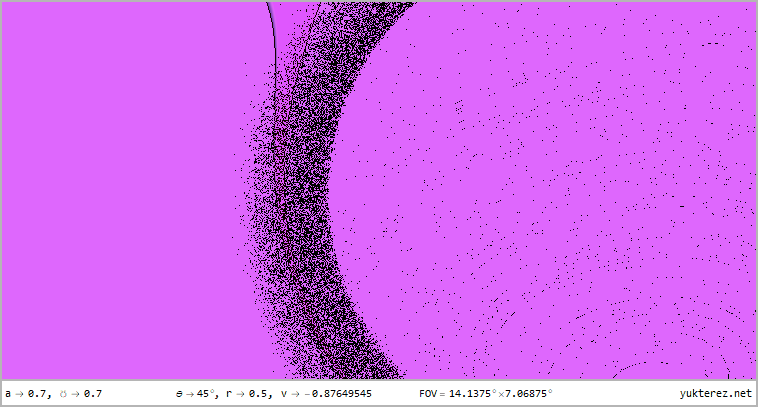
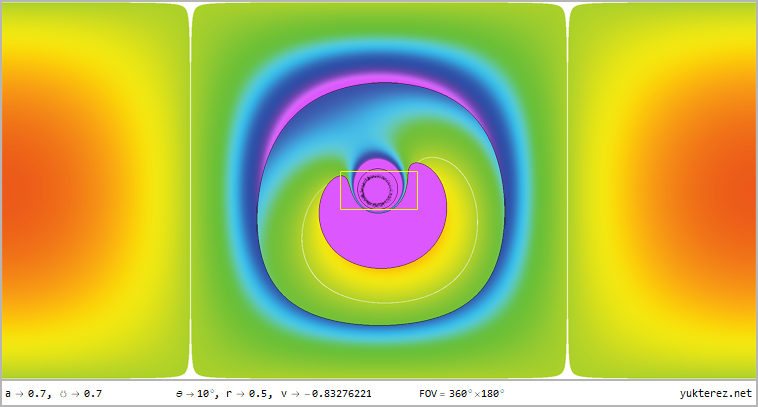
The perspectives from r=12, r=4, r=r₊ (outer horizon), r=r₋ (inner horizon) & r=0.5 for latitudes of θ=80°, θ=45° & θ=10° in
360°×180° full panorama in equirectangular projection and as stereographic projektion with front and rear view are shown, the
numeric display shows the velocities relative to a local ZAMO (at the horizons the only possible ZAMO is a photon, therefore v=c):