
 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  English versions are available on en.yukterez.net and yukipedia.
English versions are available on en.yukterez.net and yukipedia.
Verwandte Beiträge: Kerr Newman || Kerr || De Sitter || Geodäten || Gravitationslinsen || Raytracing || Flamms Paraboloid


Freier Fall in ein schwarzes Loch mit v=-c√(rₛ/r) aus der Perspektive der Freifallers. Winkeldurchmesser des Schattens: klick, Diskussion: 1 und 2


Vollpanorama des mit v=-c√(rₛ/r) hineinfallenden Beobachters im Moment in dem der Horizont überschritten wird


Rot/Blauverschiebungsprofil für den mit der negativen Fluchtgeschwindigkeit fallenden Beobachter im oberen Bild


Aberration in den Augen von drei Beobachtern auf der selben Position r=6GM/c² mit verschiedenen Geschwindigkeitsvektoren


Optische Verzerrung einer Erdkugel mit r=1.0001rₛ, Beobachter auf R=17.5rₛ: durch den Gravitationslinseneffekt ist auch die Rückseite sichtbar

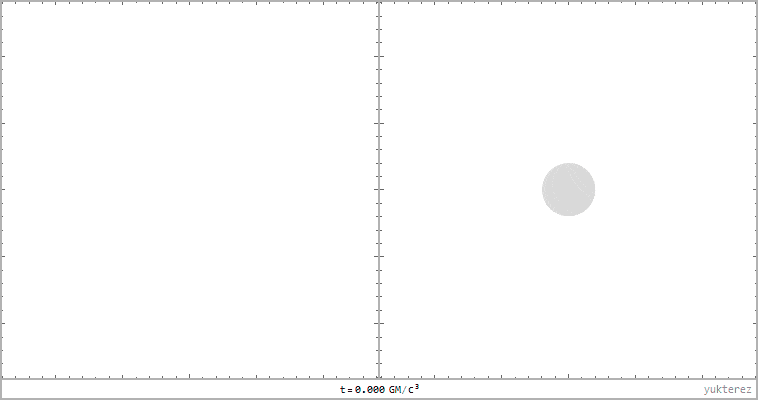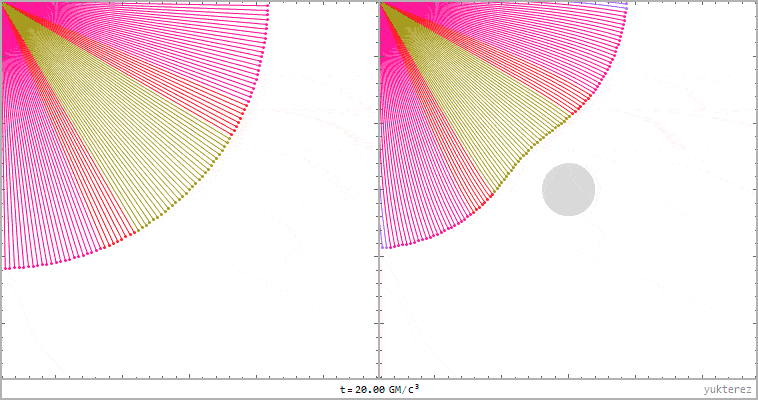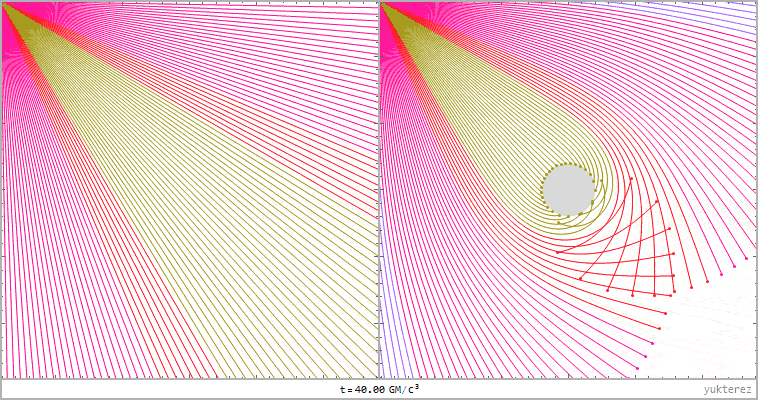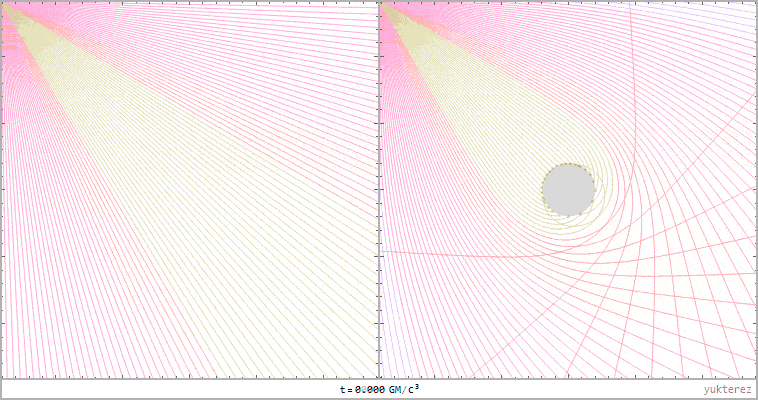
links: Strahlenbündel im flachen Minkowskiraum, rechts: Schwarzschild. Entfernung der Lichtquelle von schwarzen Loch: 20GM/c²


Strahlenbündel mit Stoßparameter b=√27≈5.2GM/c² (der scheinbare Radius des schwarzen Lochs im System eines Beobachters at infinity)


Orbit mit Periheldrehung; Startbedingungen: r₀=5, θ0=π/2, v₀=vz₀=vθ₀=51/50·√((1/5)/(1-2/5)).



Freier Fall in ein schwarzes Loch mit v=-c√(rₛ/r) aus der Perspektive der Freifallers. Winkeldurchmesser des Schattens: klick, Diskussion: 1 und 2


Vollpanorama des mit v=-c√(rₛ/r) hineinfallenden Beobachters im Moment in dem der Horizont überschritten wird


Rot/Blauverschiebungsprofil für den mit der negativen Fluchtgeschwindigkeit fallenden Beobachter im oberen Bild


Aberration in den Augen von drei Beobachtern auf der selben Position r=6GM/c² mit verschiedenen Geschwindigkeitsvektoren


Optische Verzerrung einer Erdkugel mit r=1.0001rₛ, Beobachter auf R=17.5rₛ: durch den Gravitationslinseneffekt ist auch die Rückseite sichtbar


links: Strahlenbündel im flachen Minkowskiraum, rechts: Schwarzschild. Entfernung der Lichtquelle von schwarzen Loch: 20GM/c²


Strahlenbündel mit Stoßparameter b=√27≈5.2GM/c² (der scheinbare Radius des schwarzen Lochs im System eines Beobachters at infinity)


Orbit mit Periheldrehung; Startbedingungen: r₀=5, θ0=π/2, v₀=vz₀=vθ₀=51/50·√((1/5)/(1-2/5)).



▥ Metrischer Tensor in Droste Koordinaten {t,r,θ,Ф}:


▦ Eingehende Finkelstein Koordinaten mit ť wobei dt→dť+dr(rs/r)/(1-rs/r)/c:


▧ Gullstrand-Painlevé Raindrop Koordinaten, Koordinatenzeit defininert durch die Eigenzeit von Freifallern, dt→dτ+dr√(rs/r)/(1-rs/r)/c:


Bewegungsgleichung in Schwarzschildkoordinaten; aufgrund der Kugelsymmetrie kann auf eine Winkelkoordinate reduziert werden so dass√(dθ²+sin²θ dФ²)→dθ. Damit lautet die Lösung der geodätischen Gleichung:



mit v⊥=v cos ζ als die transversale, und v∥=v sin ζ als die radiale lokale Dreiergeschwindigkeit mit dem lokalen Abschusswinkel ζ (von außen erscheint dieser aufgrund der radialen Tiefenexpansion dR>dr flacher). Bei rein radialer Bewegung vereinfacht sich die Bewegungsgleichung zu

τ ist die Eigenzeit des Testpartikels, und t die Koordinatenzeit eines Beobachters at infinty. Um die Schalenzeit eines stationären Beobachters auf r zu erhalten wird t einfach mit √(1-rs/r) multipliziert, mit dem Schwarzschildradius rs=2GM/c². Die totale Zeitdilatation ist das multiplikative Produkt aus der gravitativen und der kinematischen Zeitdilatation.
Um von der lokalen Geschwindigkeit auf die beobachtete zu transformieren gilt für die radiale und transversale Komponente:
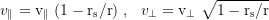
Der Betrag der lokalen bzw. verzögerten Geschwindigkeit ist dann nach Pythagoras
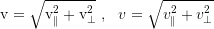
Der Drehimpuls

und die Gesamtenergie at infinity (die relativistische Masse mal der gravitativen Zeitdilatation)

sind konstant. Die lokale kinetische Energie und die potentielle Energie als Differenz der lokalen Energie zu jener at infinity ist

Effektives Potential:

Die radiale Fluchtgeschwindigkeit um von r₀ nach r₁ zu gelangen ist

womit die radiale Fluchtgeschwindigkeit in die Unendlichkeit (r₁→∞)

ist. Lokale Kreisbahngeschwindigkeit, bei der Photonensphäre auf r=3rₛ/2 die Lichtgeschwindigkeit:

Eigenzeit für den freien Fall von r₀ bis r:

Koordinatenzeit für den freien Fall von r₀ bis r:

Physikalischer Abstand zwischen zwei verschiedenen r im System des externen stationären Koordinatenbuchhalters:

Abstand vom Horizont zur Singularität im System eines mit der negativen Fluchtgeschwindigkeit einfallenden Freifallers:

in Droste Koordinaten mit grr=-1/(1-rs/r) und v=-√(rs/r) wobei γ=1/√(1-v²/c²) bzw. in Raindrop Koordinaten mit grr=-1 und v=0 wobei γ=1. Bei einem Freifall aus der Ruhelage knapp über dem Horizont ist die aufintegrierte Strecke d=πGM/c². Für die Gleichungen in anderen Koordinaten siehe hier. Simulator (mit a=℧=0 reduziert sich der Kerr Newman Simulator auf Schwarzschild): klick, für die veraltete Version in 2D das untere Feld aufklappen.

▦ Eingehende Finkelstein Koordinaten mit ť wobei dt→dť+dr(rs/r)/(1-rs/r)/c:

▧ Gullstrand-Painlevé Raindrop Koordinaten, Koordinatenzeit defininert durch die Eigenzeit von Freifallern, dt→dτ+dr√(rs/r)/(1-rs/r)/c:

Bewegungsgleichung in Schwarzschildkoordinaten; aufgrund der Kugelsymmetrie kann auf eine Winkelkoordinate reduziert werden so dass



mit v⊥=v cos ζ als die transversale, und v∥=v sin ζ als die radiale lokale Dreiergeschwindigkeit mit dem lokalen Abschusswinkel ζ (von außen erscheint dieser aufgrund der radialen Tiefenexpansion dR>dr flacher). Bei rein radialer Bewegung vereinfacht sich die Bewegungsgleichung zu

τ ist die Eigenzeit des Testpartikels, und t die Koordinatenzeit eines Beobachters at infinty. Um die Schalenzeit eines stationären Beobachters auf r zu erhalten wird t einfach mit √(1-rs/r) multipliziert, mit dem Schwarzschildradius rs=2GM/c². Die totale Zeitdilatation ist das multiplikative Produkt aus der gravitativen und der kinematischen Zeitdilatation.
Um von der lokalen Geschwindigkeit auf die beobachtete zu transformieren gilt für die radiale und transversale Komponente:
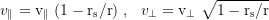
Der Betrag der lokalen bzw. verzögerten Geschwindigkeit ist dann nach Pythagoras
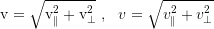
Der Drehimpuls

und die Gesamtenergie at infinity (die relativistische Masse mal der gravitativen Zeitdilatation)

sind konstant. Die lokale kinetische Energie und die potentielle Energie als Differenz der lokalen Energie zu jener at infinity ist

Effektives Potential:

Die radiale Fluchtgeschwindigkeit um von r₀ nach r₁ zu gelangen ist

womit die radiale Fluchtgeschwindigkeit in die Unendlichkeit (r₁→∞)

ist. Lokale Kreisbahngeschwindigkeit, bei der Photonensphäre auf r=3rₛ/2 die Lichtgeschwindigkeit:

Eigenzeit für den freien Fall von r₀ bis r:

Koordinatenzeit für den freien Fall von r₀ bis r:

Physikalischer Abstand zwischen zwei verschiedenen r im System des externen stationären Koordinatenbuchhalters:

Abstand vom Horizont zur Singularität im System eines mit der negativen Fluchtgeschwindigkeit einfallenden Freifallers:

in Droste Koordinaten mit grr=-1/(1-rs/r) und v=-√(rs/r) wobei γ=1/√(1-v²/c²) bzw. in Raindrop Koordinaten mit grr=-1 und v=0 wobei γ=1. Bei einem Freifall aus der Ruhelage knapp über dem Horizont ist die aufintegrierte Strecke d=πGM/c². Für die Gleichungen in anderen Koordinaten siehe hier. Simulator (mit a=℧=0 reduziert sich der Kerr Newman Simulator auf Schwarzschild): klick, für die veraltete Version in 2D das untere Feld aufklappen.


Simulator (alte Version; im aktuelleren Kerr-Simulator mit erweitertem Display kann mit a=0, crd=1 in Schwarzschild- und mit a=0, crd=2 in horizontüberschreitenden Finkelsteinkoordinaten simuliert werden):
Code: Alles auswählen
(*||| Schwarzschild Simulator |||||||| yukterez.net ||||||||||| Version 13.02.2018 |||||||| Syntax: Mathematica |||*)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
G = 1; M = 1; c = 1; rs = 2 G M/c^2; (* Einheiten *)
wp = MachinePrecision; (* numerische Genauigkeit *)
set= {"GlobalAdaptive", "MaxErrorIncreases" -> 100, Method -> "GaussKronrodRule"};
para = 20; pstep = 1/3; (* Paraboloid Grid *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
j[v_] := Sqrt[1 - v^2/c^2]; J = j[v0]; (* Gammafaktor *)
k[r_] := Sqrt[1 - rs/r]; κ = k[r0]; (* Schwarzschildfaktor *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
r0 = 3/2 rs; (* Startradius *)
v0 = 7/10 c; (* lokale Startgeschwindigkeit *)
ζ = Pi/4; (* Abschusswinkel *)
θ0 = 0; (* Startwinkel *)
τM = 20 G M/c^3; (* Simulationsdauer *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
τMax = Min[τM, plunge-0.0001]; TMax=Min[τM, и[plunge-0.0001]];
(* г = Sqrt[χ^2 + γ^2]; Θ = ArcSin[γ/г]; *) (* Kartesisch auf Polar *)
vr0 = v0 Sin[ζ] κ/J; vθ0 = v0/r0 Cos[ζ]/J; (* Längenkontraktion und Tiefenexpansion *)
d1 = τM/10; d2 = d1; f = 3; (* Schweifdauer und Frameanzahl *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
sol = NDSolve[{ (* Differentialgleichung *)
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == vr0,
r[0] == r0,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == vθ0,
θ[0] == θ0,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0,
cl'[t] == ((r'[t] / k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0
}, {r, θ, τ, cl}, {t, 0, τM},
MaxSteps -> Infinity,
Method -> Automatic,
WorkingPrecision -> wp,
InterpolationOrder -> All,
StepMonitor :> (laststep=plunge; plunge=t;
stepsize=plunge-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-5, 0, 1])}];
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
t[ξ_] := Quiet[ (* Eigenzeit nach Koordinatenzeit *)
χ /.FindRoot[Evaluate[τ[χ] /. sol][[1]] - ξ, {χ, 0}, WorkingPrecision -> wp, Method -> Automatic]];
Τ := Quiet[t[ι]];
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
grr[r_]:=If[Abs[r]>2, (1-2/Abs[r])^-1, (1-(2Abs[r]^2)/2^3)^-1];
gtt[r_]:=If[Abs[r]>2, (1-2/Abs[r])^-1, 4(3Sqrt[1-2/2]-Sqrt[1-(2Abs[r]^2)/2^3])^-2];
Ȓ[я_]:=Quiet[NIntegrate[Sqrt[Abs[grr[r]]], {r, 0, Abs[я]}, Method -> set, MaxRecursion -> 100]];
Ř[я_]:=Quiet[NIntegrate[Sqrt[Abs[grr[r]-1]], {r, Abs[я], para}, Method -> set, MaxRecursion -> 100]];
ř[я_]:=Quiet[Ř[0]-Ř[я]];
grid[я_]:=Quiet[x/.FindRoot[Ȓ[x]-я, {x, 1}]];
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
x[t_] := (Sin[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
y[t_] := (Cos[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
R[t_] := Evaluate[r[t] /. sol][[1]]; (* Radialkoordinate *)
γ[t_] := Evaluate[τ'[t] /. sol][[1]]; (* Zeitdilatation *)
и[t_] := Evaluate[τ[t] /. sol][[1]]; (* Koordinatenzeit *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
crθ[t_] := Evaluate[cl'[t] /. sol][[1]]; (* Celerität *)
vrθ[t_] := crθ[t]/Sqrt[1 + crθ[t]^2];
clr[t_] := Evaluate[r'[t] /. sol][[1]];
clθ[t_] := R[t] Evaluate[θ'[t] /. sol][[1]];
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
vr[t_] := clr[t]/γ[t]/k[R[t]]^2; (* lokale Geschwindigkeit, radial *)
vt[t_] := clθ[t]/γ[t]/k[R[t]]; (* lokale Geschwindigkeit, transversal *)
vp[t_] := Sqrt[vr[t]^2 + vt[t]^2]; (* lokale Geschwindigkeit, total *)
vc[t_] := Sqrt[vr[t]^2 k[R[t]]^2 + vt[t]^2] k[R[t]]; (* Koordinatengeschwindigkeit, total *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
s[text_] := Style[text, FontSize -> font]; font = 11; (* Stil der Anzeigetafel *)
PR = 2 r0; (* Plot Range *)
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
Do[Print[ (* Animation nach Eigenzeit *)
Rasterize[Grid[{{Show[
Graphics[{Table[{LightGray, Circle[{0, 0}, grid[n]]}, {n, pstep, para, pstep}]},
Frame -> True, ImageSize -> 360,
PlotRange -> PR, ImagePadding -> Automatic],
Graphics[{Magenta, Opacity[0.1], Annulus[{0, 0}, {2, para}]}],
Graphics[{White, Opacity[0.7], Disk[{0, 0}, 2]}],
Graphics[{Cyan, Opacity[0.1], Disk[{0, 0}, 2]}],
Graphics[{Black, Dashed, Circle[{0, 0}, r0]}],
Graphics[{PointSize[0.01], Red, Point[{x[т], y[т]}]}],
ParametricPlot[{x[η], y[η]}, {η, 0, Max[1*^-16, т - d1]},
PlotStyle->{Thickness[0.004], LightGray}],
ParametricPlot[{x[η], y[η]}, {η, Max[1*^-16, т - d2], т},
ColorFunction -> Function[{x, y, η},
Hue[0, 1, 0.5, Max[Min[(-т + (η + d2))/d2, 1], 0]]],
ColorFunctionScaling -> False]]},
{Grid[{
{s[" Eigenzeit"], " = ", s[N[т, 8]], s[" GM/c³"]},
{s[" Koordinatenzeit"], " = ", s[N[Evaluate[τ[т] /. sol][[1]], 8]], s[" GM/c³"]},
{s[" Zeitdilatation"], " = ", s[N[γ[т], 8]], s[" dt/dτ"]},
{s[" Winkel"], " = ", s[N[Evaluate[(θ[т] /. sol) 180/Pi][[1]], 8]], s[" Grad"]},
{s[" Radialkoordinate"], " = ", s[N[R[т] , 8]], s[" GM/c²"]},
{s[" x-Achse"], " = ", s[N[x[т], 8]], s[" GM/c²"]},
{s[" y-Achse"], " = ", s[N[y[т], 8]], s[" GM/c²"]},
{s[" v lokal"], " = ", s[N[vp[т], 8]], s[" c"]},
{s[" v extern"], " = ", s[N[vc[т], 8]], s[" c"]},
{s[" kinetische Energie"], " = ", s[N[1/Sqrt[1 - vp[т]^2] - 1, 8]], s[" mc²"]},
{s[" "], " ", s[" "], s[" "]}
}, Alignment -> Left, Spacings -> {0, 1/2}]}}, Alignment -> Left]]
], {т, τMax/f, τMax, τMax/f}]
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
Do[Print[ (* Animation nach Koordinatenzeit *)
Rasterize[Grid[{{Show[
Graphics[{Table[{LightGray, Circle[{0, 0}, grid[n]]}, {n, pstep, para, pstep}]},
Frame -> True, ImageSize -> 360,
PlotRange -> PR, ImagePadding -> Automatic],
Graphics[{Magenta, Opacity[0.1], Annulus[{0, 0}, {2, para}]}],
Graphics[{White, Opacity[0.7], Disk[{0, 0}, 2]}],
Graphics[{Cyan, Opacity[0.1], Disk[{0, 0}, 2]}],
Graphics[{Black, Dashed, Circle[{0, 0}, r0]}],
Graphics[{PointSize[0.01], Red, Point[{x[Τ], y[Τ]}]}],
ParametricPlot[{x[η], y[η]}, {η, 0, Max[1*^-16, Τ - d1]},
PlotStyle->{Thickness[0.004], LightGray}],
ParametricPlot[{x[η], y[η]}, {η, Max[1*^-16, Τ - d2], Τ},
ColorFunction -> Function[{x, y, η},
Hue[0, 1, 0.5, Max[Min[(-Τ + (η + d2))/d2, 1], 0]]],
ColorFunctionScaling -> False]]},
{Grid[{
{s[" Eigenzeit"], " = ", s[N[Τ, 8]], s[" GM/c³"]},
{s[" Koordinatenzeit"], " = ", s[N[ι, 8]], s[" GM/c³"]},
{s[" Zeitdilatation"], " = ", s[N[γ[Τ], 8]], s[" dt/dτ"]},
{s[" Winkel"], " = ", s[N[Evaluate[(θ[Τ] /. sol) 180/Pi][[1]], 8]], s[" Grad"]},
{s[" Radialkoordinate"], " = ", s[N[R[Τ], 8]], s[" GM/c²"]},
{s[" x-Achse"], " = ", s[N[x[Τ], 8]], s[" GM/c²"]},
{s[" y-Achse"], " = ", s[N[y[Τ], 8]], s[" GM/c²"]},
{s[" v lokal"], " = ", s[N[vp[Τ], 8]], s[" c"]},
{s[" v extern"], " = ", s[N[vc[Τ], 8]], s[" c"]},
{s[" kinetische Energie"], " = ", s[N[1/Sqrt[1 - vp[Τ]^2] - 1, 8]], s[" mc²"]},
{s[" "], " ", s[" "], s[" "]}
}, Alignment -> Left, Spacings -> {0, 1/2}]}}, Alignment -> Left]]
], {ι, TMax/f, TMax, TMax/f}]
(*|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||*)
(* Syntax: Mathematica || schwarzschild.yukterez.net || kerr.yukterez.net ||| Simon Tyran - [Симон Тыран] - Vienna *)
Verschiedene Integrationsmethoden (bei Orbits in einem Mindestabstand vom zweifachen EH reicht die Methode Automatic):
Code: Alles auswählen
Method -> {"EventLocator", "Event" -> (r[t] - 2.000001)}Code: Alles auswählen
Method -> {"StiffnessSwitching", Method -> {"ExplicitRungeKutta", Automatic}}Code: Alles auswählen
Method -> {"ImplicitRungeKutta", DifferenceOrder" -> 20}Mehrere Testpartikel:
Code: Alles auswählen
(* Schwarzschild Simulator für mehrere Testpartikel ||| schwarzschild.yukterez.net 5 2015 ||| Syntax: Mathematica *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
G = 1; M = 1; c = 1; rs = 2 G M/c^2; (* Einheiten *)
wp = MachinePrecision; (* Genauigkeit *)
para = 60; pstep = 1/2; (* Paraboloid Grid *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
j[v_] := Sqrt[1 - v^2/c^2]; (* Gammafaktor *)
k[r_] := Sqrt[1 - rs/r]; (* Schwarzschildfaktor *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
r01 = Sqrt[x01^2 + y01^2]; (* Startradius *)
y01 = +1 rs; x01 = +8 rs; (* Position *)
v01 = 0; (* lokale Startgeschwindigkeit *)
ζ1 = 0; (* Abschusswinkel *)
θ01 = ArcSin[y01/r01]; (* Startwinkel *)
r02 = Sqrt[x02^2 + y02^2]; (* Startradius *)
y02 = -1 rs; x02 = +8 rs; (* Position *)
v02 = 0; (* lokale Startgeschwindigkeit *)
ζ2 = 0; (* Abschusswinkel *)
θ02 = ArcSin[y02/r02]; (* Startwinkel *)
r03 = Sqrt[x03^2 + y03^2]; (* Startradius *)
y03 = +1 rs; x03 = +6 rs; (* Position *)
v03 = 0; (* lokale Startgeschwindigkeit *)
ζ3 = 0; (* Abschusswinkel *)
θ03 = ArcSin[y03/r03]; (* Startwinkel *)
r04 = Sqrt[x04^2 + y04^2]; (* Startradius *)
y04 = -1 rs; x04 = +6 rs; (* Position *)
v04 = 0; (* lokale Startgeschwindigkeit *)
ζ4 = 0; (* Abschusswinkel *)
θ04 = ArcSin[y04/r04]; (* Startwinkel *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
T = 100; (* Simulationsdauer *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
sol1 = NDSolve[{ (* Differentialgleichung *)
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == 0,
r[0] == r01,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == 0,
θ[0] == θ01,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0,
cl'[t] == ((r'[t] / k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0
}, {r, θ, τ, cl}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
sol2 = NDSolve[{ (* Differentialgleichung *)
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == 0,
r[0] == r02,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == 0,
θ[0] == θ02,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0,
cl'[t] == ((r'[t] / k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0
}, {r, θ, τ, cl}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
sol3 = NDSolve[{ (* Differentialgleichung *)
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == 0,
r[0] == r03,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == 0,
θ[0] == θ03,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0,
cl'[t] == ((r'[t] / k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0
}, {r, θ, τ, cl}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
sol4 = NDSolve[{ (* Differentialgleichung *)
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == 0,
r[0] == r04,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == 0,
θ[0] == θ04,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0,
cl'[t] == ((r'[t] / k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0
}, {r, θ, τ, cl}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
t1[ξ_] := Quiet[ (* Eigenzeit nach Koordinatenzeit *)
χ /.FindRoot[Evaluate[τ[χ] /. sol1][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ1 := Quiet[t1[ι]];
t2[ξ_] := Quiet[ (* Eigenzeit nach Koordinatenzeit *)
χ /.FindRoot[Evaluate[τ[χ] /. sol2][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ2 := Quiet[t2[ι]];
t3[ξ_] := Quiet[ (* Eigenzeit nach Koordinatenzeit *)
χ /.FindRoot[Evaluate[τ[χ] /. sol3][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ3 := Quiet[t3[ι]];
t4[ξ_] := Quiet[ (* Eigenzeit nach Koordinatenzeit *)
χ /.FindRoot[Evaluate[τ[χ] /. sol4][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ4 := Quiet[t4[ι]];
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
u[x_, y_] = Max[2, Sqrt[x^2 + y^2]]; (* flamm'sches Paraboloid *)
w[x_, y_] = 2 + Integrate[Sqrt[1/(1 - 2/R)], {R, 2, u[x, y]}];
q[x_, y_] = Sqrt[w[x, y]^2 - u[x, y]^2];
grid[n_] = я /. FindRoot[2 + Sqrt[(-2 + я) я] + Log[-1 + я + Sqrt[(-2 + я) я]] == R, {я, 0}];
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
x1[t_] := (Sin[Evaluate[θ[t] /. sol1]] Evaluate[r[t] /. sol1])[[1]]
y1[t_] := (Cos[Evaluate[θ[t] /. sol1]] Evaluate[r[t] /. sol1])[[1]]
x2[t_] := (Sin[Evaluate[θ[t] /. sol2]] Evaluate[r[t] /. sol2])[[1]]
y2[t_] := (Cos[Evaluate[θ[t] /. sol2]] Evaluate[r[t] /. sol2])[[1]]
x3[t_] := (Sin[Evaluate[θ[t] /. sol3]] Evaluate[r[t] /. sol3])[[1]]
y3[t_] := (Cos[Evaluate[θ[t] /. sol3]] Evaluate[r[t] /. sol3])[[1]]
x4[t_] := (Sin[Evaluate[θ[t] /. sol4]] Evaluate[r[t] /. sol4])[[1]]
y4[t_] := (Cos[Evaluate[θ[t] /. sol4]] Evaluate[r[t] /. sol4])[[1]]
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
R1[t_] := Evaluate[r[t] /. sol1][[1]]; (* Radialkoordinate *)
γ1[t_] := Evaluate[τ'[t] /. sol1][[1]]; (* Zeitdilatation *)
и1[t_] := Evaluate[τ[t] /. sol1][[1]]; (* Koordinatenzeit *)
R2[t_] := Evaluate[r[t] /. sol2][[1]]; (* Radialkoordinate *)
γ2[t_] := Evaluate[τ'[t] /. sol2][[1]]; (* Zeitdilatation *)
и2[t_] := Evaluate[τ[t] /. sol2][[1]]; (* Koordinatenzeit *)
R3[t_] := Evaluate[r[t] /. sol3][[1]]; (* Radialkoordinate *)
γ3[t_] := Evaluate[τ'[t] /. sol3][[1]]; (* Zeitdilatation *)
и3[t_] := Evaluate[τ[t] /. sol3][[1]]; (* Koordinatenzeit *)
R4[t_] := Evaluate[r[t] /. sol4][[1]]; (* Radialkoordinate *)
γ4[t_] := Evaluate[τ'[t] /. sol4][[1]]; (* Zeitdilatation *)
и4[t_] := Evaluate[τ[t] /. sol4][[1]]; (* Koordinatenzeit *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
crθ1[t_] := Evaluate[cl'[t] /. sol1][[1]];
vrθ1[t_] := crθ1[t]/Sqrt[1 + crθ1[t]^2];
clr1[t_] := Evaluate[r'[t] /. sol1][[1]];
clθ1[t_] := R1[t] Evaluate[θ'[t] /. sol1][[1]];
crθ2[t_] := Evaluate[cl'[t] /. sol2][[1]];
vrθ2[t_] := crθ2[t]/Sqrt[1 + crθ2[t]^2];
clr2[t_] := Evaluate[r'[t] /. sol2][[1]];
clθ2[t_] := R2[t] Evaluate[θ'[t] /. sol2][[1]];
crθ3[t_] := Evaluate[cl'[t] /. sol3][[1]];
vrθ3[t_] := crθ3[t]/Sqrt[1 + crθ3[t]^2];
clr3[t_] := Evaluate[r'[t] /. sol3][[1]];
clθ3[t_] := R3[t] Evaluate[θ'[t] /. sol3][[1]];
crθ4[t_] := Evaluate[cl'[t] /. sol4][[1]];
vrθ4[t_] := crθ4[t]/Sqrt[1 + crθ4[t]^2];
clr4[t_] := Evaluate[r'[t] /. sol4][[1]];
clθ4[t_] := R4[t] Evaluate[θ'[t] /. sol4][[1]];
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
vr1[t_] := clr1[t]/γ1[t]/k[R1[t]]^2; (* lokale Geschwindigkeit, radial *)
vt1[t_] := clθ1[t]/γ1[t]/k[R1[t]]; (* lokale Geschwindigkeit, transversal *)
vp1[t_] := Sqrt[vr1[t]^2 + vt1[t]^2]; (* lokale Geschwindigkeit, total *)
vc1[t_] := Sqrt[vr1[t]^2 k[R1[t]]^2 + vt1[t]^2] k[R1[t]]; (* Koordinatengeschwindigkeit, total *)
vr2[t_] := clr2[t]/γ2[t]/k[R2[t]]^2; (* lokale Geschwindigkeit, radial *)
vt2[t_] := clθ2[t]/γ2[t]/k[R2[t]]; (* lokale Geschwindigkeit, transversal *)
vp2[t_] := Sqrt[vr2[t]^2 + vt2[t]^2]; (* lokale Geschwindigkeit, total *)
vc2[t_] := Sqrt[vr2[t]^2 k[R2[t]]^2 + vt2[t]^2] k[R2[t]]; (* Koordinatengeschwindigkeit, total *)
vr3[t_] := clr3[t]/γ3[t]/k[R3[t]]^2; (* lokale Geschwindigkeit, radial *)
vt3[t_] := clθ3[t]/γ3[t]/k[R3[t]]; (* lokale Geschwindigkeit, transversal *)
vp3[t_] := Sqrt[vr3[t]^2 + vt3[t]^2]; (* lokale Geschwindigkeit, total *)
vc3[t_] := Sqrt[vr3[t]^2 k[R3[t]]^2 + vt3[t]^2] k[R3[t]]; (* Koordinatengeschwindigkeit, total *)
vr4[t_] := clr4[t]/γ4[t]/k[R4[t]]^2; (* lokale Geschwindigkeit, radial *)
vt4[t_] := clθ4[t]/γ4[t]/k[R4[t]]; (* lokale Geschwindigkeit, transversal *)
vp4[t_] := Sqrt[vr4[t]^2 + vt4[t]^2]; (* lokale Geschwindigkeit, total *)
vc4[t_] := Sqrt[vr4[t]^2 k[R4[t]]^2 + vt4[t]^2] k[R4[t]]; (* Koordinatengeschwindigkeit, total *)
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
s[text_] := Style[text, FontSize -> font]; font = 11;
Do[Print[ (* Animation nach Koordinatenzeit *)
Rasterize[Grid[{{Show[Graphics[{
{LightGray, Disk[{0, 0}, rs]}},
Frame -> True, ImageSize -> 400, PlotRange -> 1.2 Max[r01, r02, r03, r04], ImagePadding -> 1],
Graphics[Table[{Lighter[Gray], Circle[{0, 0}, grid[n]]}, {n, 2 + pstep, para, pstep}]],
Graphics[{PointSize[0.01], Red, Point[{x1[Τ1], y1[Τ1]}]}],
Graphics[{PointSize[0.01], Green, Point[{x2[Τ2], y2[Τ2]}]}],
Graphics[{PointSize[0.01], Blue, Point[{x3[Τ3], y3[Τ3]}]}],
Graphics[{PointSize[0.01], Pink, Point[{x4[Τ4], y4[Τ4]}]}]
]},
{Grid[{
{" ", s["Koordinatenzeit"], " = ", s[N[ι, 8]], s[" GM/c³"]},
{""},
{" ", s["Eigenzeit 1"], " = ", s[N[Τ1, 8]], s[" GM/c³"]},
{" ", s["Eigenzeit 2"], " = ", s[N[Τ2, 8]], s[" GM/c³"]},
{" ", s["Eigenzeit 3"], " = ", s[N[Τ3, 8]], s[" GM/c³"]},
{" ", s["Eigenzeit 4"], " = ", s[N[Τ4, 8]], s[" GM/c³"]},
{""},
{" ", s["Zeitdilatation 1"], " = ", s[N[Evaluate[τ'[Τ1] /. sol1][[1]], 8]], s[" dt/dτ"]},
{" ", s["Zeitdilatation 2"], " = ", s[N[Evaluate[τ'[Τ2] /. sol2][[1]], 8]], s[" dt/dτ"]},
{" ", s["Zeitdilatation 3"], " = ", s[N[Evaluate[τ'[Τ3] /. sol3][[1]], 8]], s[" dt/dτ"]},
{" ", s["Zeitdilatation 4"], " = ", s[N[Evaluate[τ'[Τ4] /. sol4][[1]], 8]], s[" dt/dτ"]},
{""},
{" ", s["Winkel 1"], " = ", s[N[Evaluate[(θ[Τ1] /. sol1) 180/Pi][[1]], 8]], s[" grad"]},
{" ", s["Winkel 2"], " = ", s[N[Evaluate[(θ[Τ2] /. sol2) 180/Pi][[1]], 8]], s[" grad"]},
{" ", s["Winkel 3"], " = ", s[N[Evaluate[(θ[Τ3] /. sol3) 180/Pi][[1]], 8]], s[" grad"]},
{" ", s["Winkel 4"], " = ", s[N[Evaluate[(θ[Τ4] /. sol4) 180/Pi][[1]], 8]], s[" grad"]},
{""},
{" ", s["Radialkoordinate"], " = ", s[N[Evaluate[r[Τ1] /. sol1][[1]], 8]], s[" GM/c²"]},
{" ", s["Radialkoordinate 2"], " = ", s[N[Evaluate[r[Τ2] /. sol2][[1]], 8]], s[" GM/c²"]},
{" ", s["Radialkoordinate 3"], " = ", s[N[Evaluate[r[Τ3] /. sol3][[1]], 8]], s[" GM/c²"]},
{" ", s["Radialkoordinate 4"], " = ", s[N[Evaluate[r[Τ4] /. sol4][[1]], 8]], s[" GM/c²"]},
{""},
{" ", s["x-Achse 1"], " = ", s[N[x1[Τ1], 8]], s[" GM/c²"]},
{" ", s["x-Achse 2"], " = ", s[N[x2[Τ2], 8]], s[" GM/c²"]},
{" ", s["x-Achse 3"], " = ", s[N[x3[Τ3], 8]], s[" GM/c²"]},
{" ", s["x-Achse 4"], " = ", s[N[x4[Τ4], 8]], s[" GM/c²"]},
{""},
{" ", s["y-Achse 1"], " = ", s[N[y1[Τ1], 8]], s[" GM/c²"]},
{" ", s["y-Achse 2"], " = ", s[N[y2[Τ2], 8]], s[" GM/c²"]},
{" ", s["y-Achse 3"], " = ", s[N[y3[Τ3], 8]], s[" GM/c²"]},
{" ", s["y-Achse 4"], " = ", s[N[y4[Τ4], 8]], s[" GM/c²"]},
{""},
{" ", s["v lokal 1"], " = ", s[N[vp1[Τ1], 8]], s[" c"]},
{" ", s["v lokal 2"], " = ", s[N[vp2[Τ2], 8]], s[" c"]},
{" ", s["v lokal 3"], " = ", s[N[vp3[Τ3], 8]], s[" c"]},
{" ", s["v lokal 4"], " = ", s[N[vp4[Τ4], 8]], s[" c"]},
{""},
{" ", s["v extern 1"], " = ", s[N[vc1[Τ1], 8]], s[" c"]},
{" ", s["v extern 2"], " = ", s[N[vc2[Τ2], 8]], s[" c"]},
{" ", s["v extern 3"], " = ", s[N[vc3[Τ3], 8]], s[" c"]},
{" ", s["v extern 4"], " = ", s[N[vc4[Τ4], 8]], s[" c"]}
}, Alignment -> Left, Spacings -> {0, 1/2}]}}, Alignment -> Left]]
], {ι, 1, 142, 1}]
(*/////////////////////////////////////////////////////////////////////////////////////////////////////////////////*)
(* yukterez.net *)Freifall vs Photon:
Code: Alles auswählen
G = 1; M = 1; c = 1; rs = 2 G M/c^2;
wp = MachinePrecision;
para = 24; pstep = 1/2;
j[v_] := Sqrt[1 - v^2/c^2]; J = j[v0];
k[r_] := Sqrt[1 - rs/r]; κ = k[r0];
r0 = 10;
v0 = 0;
φ = 0;
θ0 = Pi/2;
υ = 35;
vr0 = v0 Sin[φ] κ/J; vθ0 = v0/r0 Cos[φ]/J;
i[x_] := If[r[t] == 2, 1, If[r[t] < 2, Im[x], x]];
sol = NDSolve[
{r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2, r'[0] == vr0,
r[0] == r0, θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == vθ0, θ[0] == θ0,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]), τ[0] == 0,
cl'[t] == ((r'[t]/k[r[t]])^2 + (θ'[t] r[t])^2)/c^2,
cl[0] == 0}, {r, θ, τ, cl}, {t, 0, υ},
MaxSteps -> Infinity, Method -> Automatic, WorkingPrecision -> wp, InterpolationOrder -> All];
solp = NDSolve[
{r'[t] == -(1 - 2/r[t]), r[0] == 10}, r, {t, 0, 1000},
MaxSteps -> Infinity, Method -> Automatic, WorkingPrecision -> 32, InterpolationOrder -> All];
rp[τ_] := Quiet[Evaluate[r[τ] /. solp][[1]]];
тp = Quiet[tt /. FindRoot[rp[tt] - r1, {tt, 1}, WorkingPrecision -> 32]];
rf[t_] := Quiet[Evaluate[r[t] /. solf][[1]]];
T = Quiet[t /. FindRoot[rf[t] - r1, {t, 1}]];
тf = Quiet[Evaluate[τ[T] /. solf][[1]]];
t[ξ_] := Quiet[
χ /. FindRoot[
Evaluate[τ[χ] /. sol][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ:= Quiet[t[ι]];
u[b_] = b - 2;
Quiet[w[b_] = NIntegrate[Sqrt[1/(1 - 2/R)], {R, 2, b}];
q[b_] = Sqrt[w[b]^2 - u[b]^2];]
grid[n_] = я /. FindRoot[2 + Sqrt[(-2 + я) я] + Log[-1 + я + Sqrt[(-2 + я) я]] == n, {я, 0}];
x[t_] := (Sin[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
y[t_] := (Cos[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
R[t_] := Evaluate[r[t] /. sol][[1]];
γ[t_] := Evaluate[τ'[t] /. sol][[1]];
и[t_] := Evaluate[τ[t] /. sol][[1]];
crθ[t_] := Evaluate[cl'[t] /. sol][[1]]; (*Celerität*)
vrθ[t_] := crθ[t]/Sqrt[1 + crθ[t]^2];
clr[t_] := Evaluate[r'[t] /. sol][[1]];
clθ[t_] := R[t] Evaluate[θ'[t] /. sol][[1]];
vr[t_] := clr[t]/γ[t]/k[R[t]]^2;
vt[t_] := clθ[t]/γ[t]/k[R[t]];
vp[t_] := Sqrt[vr[t]^2 + vt[t]^2];
vc[t_] := Sqrt[vr[t]^2 k[R[t]]^2 + vt[t]^2] k[R[t]];
s[text_] := Style[text, FontSize -> 11]; PR = 12;
Quiet[Do[Print[
Rasterize[Grid[{{Show[
Graphics[{{Gray, Disk[{0, 0}, rs]}, {Black, Dashed,
Circle[{0, 0}, r0]}}, Frame -> True, ImageSize -> 500, PlotRange -> PR, ImagePadding -> Automatic],
Graphics[Table[{Gray, Circle[{0, 0}, grid[n]]}, {n, 2 + pstep, para, pstep}]],
Graphics[{PointSize[0.01], Green, Point[{2, 0}]}],
Graphics[{PointSize[0.01], Blue, Point[{10, 0}]}],
Graphics[{PointSize[0.01], Red, Point[{x[Quiet[t[ι + 30.553877]]], 0}]}],
Graphics[{PointSize[0.01], Green, Point[{rp[ι], 0}]}]]},
{Grid[{
{s[" Zeit A"], " = ", s[N[30.553877 + ι, 8]]},
{s[" Zeit B"], " = ", s[N[(30.553877 + ι) Sqrt[1 - 2/10], 8]]},
{s[" Zeit C"], " = ", s[N[Quiet[t[ι + 30.553877]], 8]]}},
Alignment -> Left, Spacings -> {0, 1/2}]}}, Alignment -> Left]]],
{ι, 0, 40,0.1}]]Winkeldurchmesser des Schattens:
Code: Alles auswählen
(* Angular diameter of a Schwarzschild black hole shadow, schwarzschild.yukterez.net *)
r0 = Infinity;
rs = 2; χ0 = rs/r0; χ = rs/r; p = 4/27;
α[n_] := ArcCos[(χ^2 Sqrt[1-χ0] Sqrt[χ-χ0]+n Sqrt[p(χ^3-χ^2+p)])/(χ^3-χ0 χ^2+p)] 360/π;
δ = If[D[α[-1], r]>0, Evaluate[α[+1]], Evaluate[α[-1]]];
Plot[δ, {r, 0, 10}, Frame->True,
AspectRatio->1/3, ImageSize->500,
GridLines->{Table[n, {n, 1, 10}], {45, 90, 135}},
PlotRange->{{0, 10}, {0, 180}}]
N@Block[{r=10}, δ]
N@Block[{r=0.0000001}, δ]
























