Kerr-Newman, second order differential equations of motion for a charged particle and photons. Animations by Simon Tyran, Vienna (Yukterez)
This is the english version. 
Deutschsprachige Version auf kerr.newman.yukterez.net und Yukipedia.
←Shadow of an extremal Kerr-Newman BH with a²+℧²=M², Angle of view: edge on. For other parameters see here. Raw material: Commons.
←Zoom with overlayed ergoshphere and horizon surfaces. Comparison with an uncharged Kerr black hole: click here
←Accretion disk around a spinning and charged BH with a=0.95, ℧=0.3, ri=isco, ra=10, viewpoint=89°. Earth surface at r=1.01r+.
←Kretschmann scalar, cartesian projektion. The areas around the poles are curved negatively, and those around the equator positively.
←Retrograde orbit of a charged particle (q=1) around a BH with spin & charge a=√¾ & ℧=⅓. v0 & i0: local initial velocity & inclination
←Prograde orbit of a neutral testparticle around a spinning and electrically charged black hole with spin a=0.9 and charge ℧=0.4
←Prograde orbit of a negatively charged testparticle around a spiining and positively charged black hole with the same parameters as above
←Nonequatorial and retrograde photon orbit around a spinning (a=½) and charged (℧=½) black hole, constant Boyer Lindquist radius
←Polar photon orbit around a spinning (a=0.5) and charged (℧=0.75) naked singularity, constant Boyer Lindquist radius
←Polar orbit (Lz=0) of a positively charged testpaticle (q=⅓) around a positively charged and spinning black hole (℧=a=0.7)
←Plunge orbit of a negative particle (q=-⅓), BH like above. The nonpolar axial velocity for q<0 is positive for Lz=0 due to electric force.
←Free fall of a neutral testparticle around a rotating and charged naked singularity with spin a=1.5 and electric charge ℧=0.4
←Geodesic orbit around a naked Kerr Newman ringsingularity with the same spin and charge parameters as in the last example
←Nonequatorial and retrograde photon orbit around a naked singularity spinning with a=0.9 and charged with ℧=0.9
←Retrograde photon orbit around a naked singularity (a=0.99, ℧=0.99). Local equatorial inclination angle: -2.5rad=-143.23945°
←Stationary photon orbit (E=0) around a ringsingularity (a=½, ℧=1). Except at r=1, θ=90° v framedrag is <c everywhere, therefore no ergospheres.
←Equatorial retrograde photon orbit, singularity at r=0→R=√(r²+a²)=a=½. Ergoring (green) at r=1, turning points at r=0.8 and r=1.3484
←Retrograde photon orbit of the third kind insinde a spinning (a=0.75) and charged (℧=0.5) black hole, constant BL radius
←Retrograde (but due to superluminal frame dragging apparently prograde) photon orbit inside a BH with a=℧=0.707 at r=0.8
←Orbit of a negatively charged particle inside a positively charged Reissner Nordström black hole (also see Dokuchaev, Fig. 1)
Line element in Boyer Lindquist coordinates, metric signature (+,-,-,-):
Shorthand terms:
with the spin parameter â=Jc/G/M or in dimensionless units a=â/M, the specific electric charge Ω=⚼·√(K/G) and the dimensionless charge ℧=Ω/M. Here we use the units G=M=c=K=1 with lengths in GM/c² and times in GM/c³. The relation between the mass-equivalent of the total energy and the irreducible mass Mirr is
Effective mass:
For testparticles with mass μ=-1, for photons μ=0. The specific charge of the test particle is q. Transformation rule for co- and contravariant indices (superscripted letters are not powers but indices):
Co- and contravariant metric:
Elektromagnetic potential:
Covariant elektromagnetic tensor:
Contravariant Maxwell-tensor:
with the Christoffel symbols:
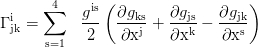
the second proper time derivatives of the coordinates are:
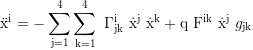
Equations of motion:
Canonical 4-momentum, local 3-velocity and 1st proper time derivatives:
From the line element:
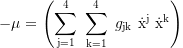
we get the total time dilation of a neutral particle:
Total time dilation of a charged particle:
Relation between the first time derivatives and the covariant momentum components:
Relation between the first time derivatives and the local three-velocity components:
with the contracted electromagnetic potential
The radial effective potential which defines the turning points at its zero roots is
and the latitudinal potential
with the parameter
For the 3-velocity relative to a local ZAMO we take E and solve for v:
or divide the gravitational time dilation by the total time dilation to get the inverse of the Gamma factor:
Radial escape velocity for a neutral particle:
For the escape velocity of a charged particle with zero orbital angular momentum we set E=1 and solve for v:
1. Constant of motion: Total energy E=-pt
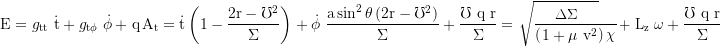
2. Constant of motion: axial angular momentum Lz=+pφ
3. Constant of motion: Carter's constant
with the coaxial component of the angular momentum, which itself is not a constant:
Radial momentum component:
The azimuthal and latitudinal impact parameters are
Gravitative time dilatation of a corotating neutral ZAMO, infinite at the horizon:
Time dilation of a stationary particle, infinite at the ergosphere:
Frame-dragging angular velocity observed at infinity:
Local frame-dragging velocity relative to the fixed stars (c at the ergosphere):
with the relation
Axial and coaxial radius of gyration:
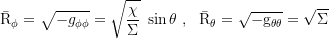
Axial and coaxial circumference:
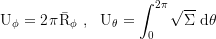
The radii of the equatorial photon orbits are given implicitly by:
The innermost stable orbit (ISCO) of a neutral particle is given by:
Radial coordinates of the horizons and ergospheres:
Cartesian projection:
r in relation to x,y,z:
Cartesian radius:
Cartesian latitude:
Transformation rule from Boyer Lindquist to Doran Raindrop:
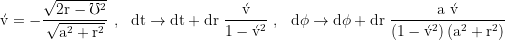
Relative to a local ZAMO the river of space has the negative radial escape velocity:
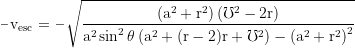
Metric tensor in Doran Raindrop coordinates, covariant:
Contravariant metric tensor:
Elektromagnetic vector potential:
Covariant Maxwell-tensor:
Contravariant elektromagnetic tensor:
Total velocity relative to a local raindrop:
Radial local velocity:
Latitudinal local velocity:
Longitudinal local velocity:
Coordinate time differential:
More details: this way, comparison Boyer Lindquist with Raindrop Doran (animation and plots): click, other coordinates: geodesics.yukterez.net, view from the inside of a black hole: click
Horizons and ergospheres in pseudospherical (r,θ,φ) and cartesian (x,y,z) coordinates:
Simulator code: original / backup, other coordinates: click here
images and animations by Simon Tyran, Vienna (Yukterez) - reuse permitted under the Creative Commons License CC BY-SA 4.0
